|
"
0
C
F
G
H
K
L
N
P
S
T
W
Z
А
Б
В
Г
Д
Е
Ж
З
И
Й
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Ш
Э
Ю
Я
КРАЕВАЯ ЗАДАЧАЗначение КРАЕВАЯ ЗАДАЧА в математической энциклопедии: для уравнения с частными производными - задача определения в нек-рой области Dпеременных 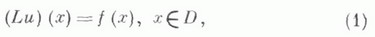 удовлетворяющего на границе Sэтой области (или ее части) определенным краевым условиям  Как правило, краевые условия связывают граничные значения решения с его производными до нек-рого порядка, т. е. Вявляется дифференциальным оператором. Однако встречаются и краевые условия других типов. Для данного дифференциального уравнения целесообразность рассмотрения той или иной К. з. часто определяется понятием ее корректной постановки. Именно, К. з. корректно поставлена, если ее решение существует, единственно и непрерывно зависит от данных этой задачи. Различные типы дифференциальных уравнений требуют различных корректно поставленных К. з., и обратно, корректные постановки К. з. иногда могут служить основой для классификации типов дифференциальных уравнений. К. з. наз. линейной, если операторы Lи Влинейны, и однородной, если fи j в (1), (2) равны нулю. Линейная К. з. наз. нётеровой, если: а) однородная задача имеет конечное число kлинейно независимых решений; б) неоднородная задача разрешима тогда и только тогда, когда f и j удовлетворяют lлинейно независимым условиям типа условий ортогональности; в) при условии однозначной разрешимости решение непрерывно зависит от f и j. Если k=l, то задача наз. фредгольмовой. Разность k-lопределяет индекс задачи. Широкий класс К. з. для линейных уравнений с частными производными 2-го порядка  охватывается задачей Пуанкаре. В этой задаче носителем краевых условий является вся граница, к-рая предполагается ( п-1)-мерным многообразием, а граничный оператор Вв (2) имеет вид  Задача Пуанкаре хорошо исследована в ограниченной области Dс достаточно гладкой границей, при условии равномерной эллиптичности оператора L. В предположении достаточной гладкости коэффициентов операторов L и В в (3), (4) и границы области Dзадача Пуанкаре нётерова, если Для общего эллиптич. уравнения порядка 2m 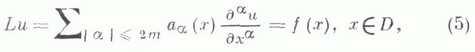 краевые условия могут задаваться с помощью линейных дифференциальных операторов 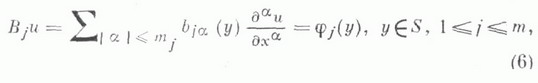 порядка Другой тип К. з. представляют так наз. смешанные задачи, в к-рых на смежных участках границы задаются различные краевые условия. Для эллиптич. уравнений характерно то, что краевые условия задаются на всей границе. Однако в полной мере это относится только к равномерно эллиптич. уравнениям. Если оператор Lв (3) эллиптичен внутри области и на части Если уравнение (3) не принадлежит к эллиптич. типу, то часть границы от задания краевых условий, как правило, освобождается. Напр., для простейшего уравнения параболич. типа - уравнения теплопроводности 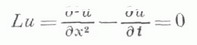 задача Дирихле в области D, ограниченной прямыми Специальным образом ставятся К. з. для уравнений смешанного эллиптико-типерболич. типа. Важное место занимают К. з. в теории аналитич. функций. Пусть S - кусочно гладкая линия на плоскости, т. е. объединение конечного числа простых ориентируемых дуг. Задача линейного сопряжения заключается в определении аналитической вне Sфункции 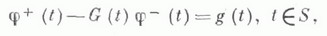 где G(t).и g(t) - заданные функции. С помощью представлений аналитич. функций интегралами типа Коши при некоторых предположениях относительно функций G, gи линии Sрешения этой задачи выписываются в явном виде. См. Граничные задачи теории аналитических функций. Для изучения К. з. предложен ряд методов. Шварца альтернирующий метод и связанные с ними выметания метод Пуанкаре и Перрона метод опираются на применение принципа максимума. Решение К. з. с помощью интегральных уравнений основано на различных интегральных представлениях решений. Исследование К. з. с помощью априорных оценок относится к функциональным методам. Широко применяется теория обобщенных функций. В практических приложениях значительное распространение получили различные конечноразностные методы. Лит.: [1] Б е р с Л., Джон Ф., Ш е х т е р М., Уравнения с частными производными, пер. с англ., М., 1966; [2] Бицадзе А. В., Краевые задачи для эллиптических уравнений второго порядка, М., 1966; [3] К у р а н т Р., Уравнения с частными производными, пер. с англ., М., 1964; [4] Ладыженская О. А., Краевые задачи математической физики, М., 1973; [5] М и р а н д а К., Уравнения с частными производными эллиптического типа, пер. с итал., М,, 1957: [6] Мусхелишвили Н. И., Сингулярные интегральные уравнении, 3 изд., М., 1968; [7] Т и х о н о в А. Н., Самарский А. А., Уравнения математической физики, 4 изд., М., 1972. А. П. Солдатов. |
|
|
|

 решения u(x) уравнения
решения u(x) уравнения  и фредгольмова, если
и фредгольмова, если 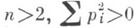 _ и вектор
_ и вектор  некасателен к 5. При исследовании задачи Пуанкаре в двумерном случае широкое применение находят методы теории функций комплексного переменного (см. Краевая задача;методы комплексного переменного).
некасателен к 5. При исследовании задачи Пуанкаре в двумерном случае широкое применение находят методы теории функций комплексного переменного (см. Краевая задача;методы комплексного переменного).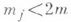 с коэффициентами, определенными на границе Sобласти D. Если операторы Lи В j удовлетворяют так наз. условию дополнительности, то производные порядка 2m функции н, удовлетворяющей граничным условиям, можно оценить (в нек-рой норме) через норму f в (5) и подходящие нормы граничных функций
с коэффициентами, определенными на границе Sобласти D. Если операторы Lи В j удовлетворяют так наз. условию дополнительности, то производные порядка 2m функции н, удовлетворяющей граничным условиям, можно оценить (в нек-рой норме) через норму f в (5) и подходящие нормы граничных функций 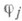 в (6). К. з. такого типа наз. коэрцитивными К. з.
в (6). К. з. такого типа наз. коэрцитивными К. з. параболически вырождается, то в зависимости от характера вырождения участок S0 от задания краевых условий может освобождаться. См. также Краевая задача для эллиптического уравнения.
параболически вырождается, то в зависимости от характера вырождения участок S0 от задания краевых условий может освобождаться. См. также Краевая задача для эллиптического уравнения.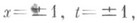 состоит в задании граничных значений функции ина отрезках
состоит в задании граничных значений функции ина отрезках 

 имеющей предельные значения
имеющей предельные значения  с обеих сторон Sи удовлетворяющей краевому условию
с обеих сторон Sи удовлетворяющей краевому условию