"
0
C
F
G
H
K
L
N
P
S
T
W
Z
А
Б
В
Г
Д
Е
Ж
З
И
Й
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Ш
Э
Ю
Я
КОЯДРОЗначение КОЯДРО в математической энциклопедии:
морфизма категории - понятие, двойственное понятию ядра морфизма. В категориях векторных пространств, групп, колец и т. п. оно описывает наибольший факторобъект объекта В, аннулирующий образ гомоморфизма 
Пусть  - категория с нулевыми морфизмами. Морфизм - категория с нулевыми морфизмами. Морфизм  наз. коядром морфизма наз. коядром морфизма  если если  и всякий морфизм и всякий морфизм  для к-рого для к-рого  однозначно представим в виде однозначно представим в виде 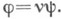 К. морфизма К. морфизма  обозначается обозначается 
Если 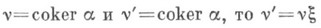 для единственного изоморфизма для единственного изоморфизма 
Обратно, если  - изоморфизм, то - изоморфизм, то  есть К. морфизма а. Таким образом, все К. морфизма а образуют факторобъект объекта В, к-рый обозначается есть К. морфизма а. Таким образом, все К. морфизма а образуют факторобъект объекта В, к-рый обозначается 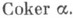 Если Если 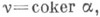 то v - нормальный эпиморфизм. Обратное, вообще говоря, неверно. К. нулевого морфизма то v - нормальный эпиморфизм. Обратное, вообще говоря, неверно. К. нулевого морфизма  равно равно  К. единичного морфизма 1A существует тогда и только тогда, когда в К. единичного морфизма 1A существует тогда и только тогда, когда в  имеется нулевой объект. имеется нулевой объект.
В категории  с нулевым объектом морфизм с нулевым объектом морфизм  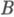 обладает К. в том и только в том случае, когда в обладает К. в том и только в том случае, когда в  существует коуниверсальный квадрат относительно морфизмов существует коуниверсальный квадрат относительно морфизмов  Это условие выполнено, в частности, для любого морфизма локально малой справа категории с нулевым объектом и произведениями. Это условие выполнено, в частности, для любого морфизма локально малой справа категории с нулевым объектом и произведениями.
М. Ш. Цаленко.
|


 - категория с нулевыми морфизмами. Морфизм
- категория с нулевыми морфизмами. Морфизм  наз. коядром морфизма
наз. коядром морфизма  если
если  и всякий морфизм
и всякий морфизм  для к-рого
для к-рого  однозначно представим в виде
однозначно представим в виде 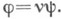 К. морфизма
К. морфизма  обозначается
обозначается 
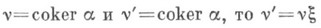 для единственного изоморфизма
для единственного изоморфизма 
 - изоморфизм, то
- изоморфизм, то  есть К. морфизма а. Таким образом, все К. морфизма а образуют факторобъект объекта В, к-рый обозначается
есть К. морфизма а. Таким образом, все К. морфизма а образуют факторобъект объекта В, к-рый обозначается 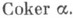 Если
Если 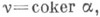 то v - нормальный эпиморфизм. Обратное, вообще говоря, неверно. К. нулевого морфизма
то v - нормальный эпиморфизм. Обратное, вообще говоря, неверно. К. нулевого морфизма  равно
равно  К. единичного морфизма 1A существует тогда и только тогда, когда в
К. единичного морфизма 1A существует тогда и только тогда, когда в  имеется нулевой объект.
имеется нулевой объект. с нулевым объектом морфизм
с нулевым объектом морфизм 
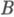 обладает К. в том и только в том случае, когда в
обладает К. в том и только в том случае, когда в  существует коуниверсальный квадрат относительно морфизмов
существует коуниверсальный квадрат относительно морфизмов  Это условие выполнено, в частности, для любого морфизма локально малой справа категории с нулевым объектом и произведениями.
Это условие выполнено, в частности, для любого морфизма локально малой справа категории с нулевым объектом и произведениями.