" 0 C F G H K L N P S T W Z А Б В Г Д Е Ж З И Й К Л М Н О П Р С Т У Ф Х Ц Ч Ш Э Ю Я

АППРОКСИМАТИВНАЯ НЕПРЕРЫВНОСТЬ

Значение АППРОКСИМАТИВНАЯ НЕПРЕРЫВНОСТЬ в математической энциклопедии:

обобщение понятия непрерывности с заменой обычного предела на аппроксимативный предел. Функция f(x).наз. аппроксимативно непрерывной в точке , если

В простейшем случае - действительная функция точки п-мерного евклидова пространства (в более общем случае - вектор-функция). Справедливы следующие теоремы. 1) Действительная функция измерима по Лебегу на множестве E в том и только том случае, если она аппроксимативно непрерывна почти всюду на Е (теорема Данжуа -Степанова). 2) Для любой ограниченной измеримой по Лебегу функции в каждой точке ее А. н.

где есть n-мерная мера Лебега, 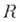- содержащий точку n-мерный невырожденный сегмент, 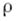- его диаметр.

Лит.:[1] Сакс С., Теория интеграла, пер. с англ., М., 1949. Г. П. Толстое.