|
"
0
C
F
G
H
K
L
N
P
S
T
W
Z
А
Б
В
Г
Д
Е
Ж
З
И
Й
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Ш
Э
Ю
Я
КОШИ - КОВАЛЕВСКОЙ ТЕОРЕМАЗначение КОШИ - КОВАЛЕВСКОЙ ТЕОРЕМА в математической энциклопедии: теорема, утверждающая существование (единственного) аналитич. решения задачи Коши в малом, если функции, задающие дифференциальное уравнение или систему этих уравнений и все начальные данные вместе с их нехарактеристическим носителем, являются аналитическими. Для системы kдифференциальных уравнений с частными производными с kнеизвестными функциями 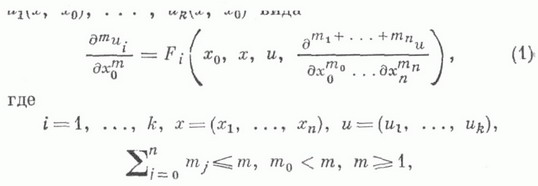 К. - К. т. формулируется следующим образом: задача Коши  где Пусть дана линейная система дифференциальных уравнений вида 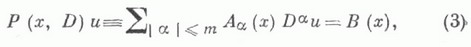 где 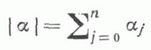 - порядок дифференциального оператора - порядок дифференциального оператора  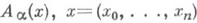 - заданная квадратная матрица - заданная квадратная матрица порядка Вообще говоря, К.- К. т. не исключает существования неаналитических, помимо аналитического, решений задачи Коши. Однако для линейной системы дифференциальных уравнений (3) с аналитич. оэффициентами Решение задачи Коши (1), (2), существование к-рого гарантируется К.- К. т., может оказаться неустойчивым (т. к. малое изменение начальных данных jij(x). может вызвать сильное изменение решения), напр., в том случае, когда система (1) принадлежит эллиптич. типу. При неаналитических начальных данных задача Коши (1), (2) может потерять смысл, если не ограничиться случаем, когда система (1) является гиперболической. К.- К. т. для широкого класса уравнений обобщена на случай, когда начальное многообразие является характеристическим в каждой точке (см. [1], [2]). В этом случае начальные функции не могут быть заданы произвольно; они должны удовлетворять определенным условиям, к-рые диктуются дифференциальным уравнением. Характеристическая задача Коши может иметь неединственное решение. В частности, имеет место следующее утверждение. Пусть Р( х, D) - дифференциальный оператор порядка тс главной частью  Если начальное многообразие является характеристическим вдоль нек-рых кривых, то, вообще говоря, решение характеристич. задачи Коши многозначно в нек-рой окрестности начальной поверхности и степень ветвления определяется геометрич. природой соответствующих характеристич. поверхностей. Теорема доказана С. В. Ковалевской (1875). Лит.:[1] Б е р с Л., Джон Ф., Ш е х т е р М., Уравнения с частными производными, пер. с англ., М., 1966; [2] Б и ц а д з е А. В., Уравнения математической физики, М., 1976; 13] Владимиров В. С., Уравнения математической физики, 2 изд., М., 1971; [4] К у р а н т Р., Уравнения с частными производными, пер. с англ., М., 1964; [5] Хёрмандер Л., Линейные дифференциальные операторы с частными производными, пер. с англ., М., 1965. А. М. Нахушев. |
|
|
|

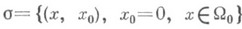 - носитель начальных данных
- носитель начальных данных 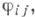 всегда имеет и притом единственное аналитич. решение и( х, х 0). в нек-рой области W пространства переменных х 0,х, содержащей
всегда имеет и притом единственное аналитич. решение и( х, х 0). в нек-рой области W пространства переменных х 0,х, содержащей 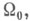 если
если 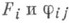 являются аналитич. функциями всех своих аргументов.
являются аналитич. функциями всех своих аргументов.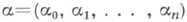 - вектор с неотрицательными, целочисленными координатами;
- вектор с неотрицательными, целочисленными координатами;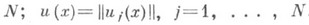 , - искомый вектор-столбец; В(х).- заданный вектор с Nкомпонентами.
, - искомый вектор-столбец; В(х).- заданный вектор с Nкомпонентами. и условиями Коши на аналитической нехаракте-ристич. поверхности
и условиями Коши на аналитической нехаракте-ристич. поверхности  задача Коши имеет не более одного решения в нек-рой окрестности
задача Коши имеет не более одного решения в нек-рой окрестности 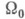 поверхности s.При этом не предполагается аналитичность начальных данных и решения и(х].
поверхности s.При этом не предполагается аналитичность начальных данных и решения и(х].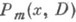 и с вещественными аналитич. оэффициентами, определенный в окрестности W точки х 0 из евклидова пространства
и с вещественными аналитич. оэффициентами, определенный в окрестности W точки х 0 из евклидова пространства 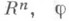 - вещественная аналитическая в W функция такая, что
- вещественная аналитическая в W функция такая, что 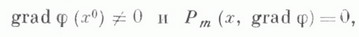 но
но 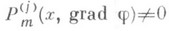 для некоторого j при х=х 0. Тогда существует такая окрестность
для некоторого j при х=х 0. Тогда существует такая окрестность  точки х 0 и аналитическая при
точки х 0 и аналитическая при 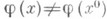 функция и(х).из класса
функция и(х).из класса  что Р( х, b) и=0 и . .
что Р( х, b) и=0 и . .