|
"
0
C
F
G
H
K
L
N
P
S
T
W
Z
А
Б
В
Г
Д
Е
Ж
З
И
Й
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Ш
Э
Ю
Я
КОШИ НЕРАВЕНСТВОЗначение КОШИ НЕРАВЕНСТВО в математической энциклопедии: - 1) К. н.- неравенство для конечных сумм, имеющее вид:.. 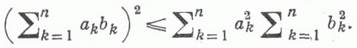 Доказано О. Коши (A. Cauchy, ;1821); интегральный аналог - Буняковского неравенство. 2) К. н.- неравенство для модуля  К. н. имеют вид  где r - радиус любого круга 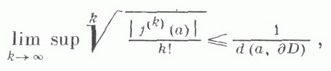 где  Для голоморфной функции f(z) многих комплексных переменных  где с k, . kn - коэффициенты разложения f(z) в степенной ряд  r1, ..., r п - радиусы поликруга Лит. см. при ст. Коши - Адамара теорема. Е. Д. Соломенцев. |
|
|
|

 производной регулярной аналитич. функции
производной регулярной аналитич. функции 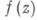 в фиксированной точке акомплексной плоскости С или для модуля коэффициента
в фиксированной точке акомплексной плоскости С или для модуля коэффициента 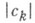 разложения f(z) в степенной ряд
разложения f(z) в степенной ряд  на к-ром функция f(z) регулярна; М(r) - максимум модуля
на к-ром функция f(z) регулярна; М(r) - максимум модуля  на окружности
на окружности  Неравенства (*) встречаются в работах О. Коши (А. Cauchy, см., напр., [1]). Из них непосредственно Вытекает неравенство Коши - Адамара (см. [2]):
Неравенства (*) встречаются в работах О. Коши (А. Cauchy, см., напр., [1]). Из них непосредственно Вытекает неравенство Коши - Адамара (см. [2]):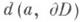 - расстояние от точки адо границы
- расстояние от точки адо границы  области голоморфности функции f(z). В частности, для целой функции f(z) в любой точке
области голоморфности функции f(z). В частности, для целой функции f(z) в любой точке  имеем
имеем  К. н. имеют вид
К. н. имеют вид 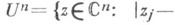
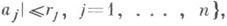 на к-ром f(z) голоморфна; M(r1, ..., r п) - максимум
на к-ром f(z) голоморфна; M(r1, ..., r п) - максимум  на остове поликруга Un.
на остове поликруга Un.