КОШИ ЗАДАЧА

Значение КОШИ ЗАДАЧА в математической энциклопедии:

численные методы решения для обыкновенного дифференциального уравнения. Задачей Коши наз. задача определения функции или нескольких функций, удовлетворяющих одному или, соответственно, системе дифференциальных уравнений и принимающих заданные значения в нек-рой фиксированной точке. Пусть

- вектор-функции, определенные и непрерывные соответственно на отрезке и в замкнутой области где - некоторая норма в конечномерном пространстве Rⁿ. В этих обозначениях К. з. для системы обыкновенных дифференциальных уравнений 1-го порядка записывается в виде

Вводя соответствующим образом новые неизвестные функции, можно привести к такому виду К. з. для любой системы обыкновенных дифференциальных уравнений произвольного порядка. Решение задачи (1) существует, если функция f(x, у).непрерывна в П. Для того чтобы это решение было единственным, достаточно, чтобы выполнялось условие О т к у д а: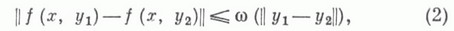

где функция w(t) - такова, что

или более сильное условие Липшица: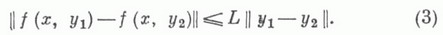

Величина Lназ. постоянной Липшица. Если функция f(x, у).непрерывно дифференцируема по у, то в качестве постоянной Липшица можно взять величину

Оценка (3) с постоянной Липшица (4) оказывается в ряде случаев слишком грубой для успешного применения численных методов решения К. з., несмотря на то, что теоретически решение этой задачи существует и оно единственно. Это происходит, в частности, в тех случаях, когда собственные значения матрицы имеют "большой разброс", т. е. наибольшее собственное значение в сотни или даже тысячи раз больше наименьшего собственного значения. Такие системы, дифференциальных уравнений наз. жесткими системами, а соответствующие задачи - жесткими задачами Кош и. Одним из источников возникновения жестких систем является сведение уравнений с частными производными к системе обыкновенных дифференциальных уравнений, напр. с помощью метода прямых.

Численные методы для обыкновенных дифференциальных уравнений представляют собой, как правило, одно или несколько соотношений, связывающих искомую функцию у(х).в дискретной последовательности точке х _k, k=0, 1, ..., множество к-рых наз. сеткой. Основы численных методов вообще и для дифференциальных уравнений в частности были заложены Л. Эйлером (L. Euler). Его именем называется один из самых простых методов решения К. з., к-рый состоит в следующем. Пусть решение задачи (1) в окрестности точки х _k разложено в ряд Тейлора

Если величина х-х _k, мала, то, отбрасывая члены порядка ( х-x_k)² и более высокого, получают приближенное равенство

В точке x_k+1 приближенное решение может быть вычислено по формуле

Это соотношение и наз. методом Эйлера.

В дальнейшем численные методы были значительно усовершенствованы. Это развитие велось в основном в двух направлениях: методы, получившие в дальнейшем название Рунге-Кутта методов и конечноразностные методы, важнейшим представителем к-рых является Адамса метод.

К достоинствам методов Рунге - Кутта следует отнести то, что алгоритмы, получающиеся на их основе, являются однородными, т. е. не изменяющимися при переходе от одной точки сетки к другой. Кроме того, в методах Рунге - Кутта можно изменять шаг интегрирования в соответствии с требуемой точностью вычислений без значительного усложнения самого алгоритма (см. Кутта - Мерсона метод, Рунге правило). На основе этих методов созданы достаточно надежные двусторонние методы. Основным недостатком является то, что для вычисления приближенного решения в одной точке сетки требуется несколько вычислений правой части f(x, у).дифференциального уравнения (1). Это приводит, в особенности при сложных правых частях, к значительному увеличению времени вычислений.

В конечноразностных методах, в том числе в методе Адамса, требуется лишь одно вычисление правой части на один узел сетки. Это является главным достоинством конечноразностных методов. Однако для того чтобы начать вычисления по какой-либо конечноразностной формуле, необходимо прежде вычислить дополнительные "начальные значения". Это приводит к тому, что алгоритм оказывается неоднородным - первые несколько значений должны вычисляться по другим формулам. Более существенным недостатком конечноразностных методов является невозможность простого изменения шага интегрирования, т. е. необходимость использовать сетки с постоянным шагом.

На основе конечноразностных методов разработаны так. наз. методы предсказания - уточнения, к-рые представляют собой пару конечноразностных формул, одна из к-рых (предсказывающая) является, как правило, явной, а вторая (уточняющая) - неявной, напр., предсказывающая:

уточняющая:

Предсказывающе-уточняющие методы находят успешное применение при решении жестких систем обыкновенных дифференциальных уравнений. Несмотря на то, что дифференциальные уравнения высокого порядка формально сводятся к системе уравнений 1-го порядка, методы, приспособленные к конкретному виду дифференциального уравнения, иногда оказываются значительно более эффективными. В связи с этим развиваются конечноразностные методы, использующие производные высшего порядка, напр. Штермера метод.

Лит.:[1] Б е р е з и н И. С., Ж и д к о в Н. П., Методы вычислений, 2 изд., т. 2, М., 1962; [2] Бахвалов Н. С., Численные методы, 2 изд., М., 1975; [3] Modern Numerical Methods for ordinary differential equations, Oxf., 1976.

В. В. Поспелов.