|
"
0
C
F
G
H
K
L
N
P
S
T
W
Z
А
Б
В
Г
Д
Е
Ж
З
И
Й
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Ш
Э
Ю
Я
КОШИ ЗАДАЧАЗначение КОШИ ЗАДАЧА в математической энциклопедии: - одна из основных задач теории дифференциальных уравнений (обыкновенных и с частными производными); состоит в отыскании решения (интеграла) дифференциального уравнения, удовлетворяющего так наз. начальным условиям (начальным данным). К. з. обычно возникает при анализе процессов, определяемых дифференциальным законом и начальным состоянием, математич. выражением к-рых и являются уравнение и начальное условие (откуда терминология и выбор обозначений: начальные данные задаются при (=0, а решение отыскивается при Основные вопросы, к-рые связаны с К. з., таковы. 1) Существует ли (хотя бы локально) решение К. з.? 2) Если решение существует, то какому пространству оно принадлежит, в частности, какова область его существования? 3) Является ли решение единственным? 4) Если решение единственно, то будет ли оно корректным, т. е. непрерывным (в каком-либо смысле) относительно начальных данных? Простейшая К. з. состоит в том, что требуется найти определенную на полупрямой  (а - данная функция) и при х=х 0 принимает значение и 0:  Геометрически это означает, что в семействе интегральных кривых уравнения (1) на плоскости ( х, и).разыскивается кривая, преходящая через точку ( х 0, u0). Первое утверждение о существовании такой функции (при условии непрерывности f для всех хи непрерывной дифференцнруемости ее по и).доказано О. Коши (A.Cauchy, 1820-30) и обобщено Э. Пикаром (Е. Picard, 1891-96) (заменившим дифференцируемость условием Липшица по и). При этом решение К. з. оказывается единственным и непрерывно зависящим от начальных данных. Современные представления о К. з. - по существу далеко идущее обобщение этой задачи. То, что вопросы 1) - 4) глубоко затрагивают суть дела, т. е. для утвердительного ответа на них требуются определенные условия, иллюстрируется уже теорией обыкновенных дифференциальных уравнений. Так, решение К. з. для уравнения (1) с условием (2), где f задана на открытом множестве G и лишь непрерывна, существует на нек-ром интервале, зависящем от Gи (х 0, u0) (см. Пеана теорема), но может быть неединственным. Решение может существовать не во всех точках, где определено f. Дословно так же формулируется К. з. для систем обыкновенных дифференциальных уравнений, т. е. для обыкновенного дифференциального уравнения вида (1) с начальным условием (2), где и=и (х).- функция со значением в конечномерном векторном пространстве Для обыкновенных дифференциальных уравнений высших порядков 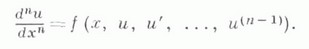 К. з ., в начальных данных к-рой участвуют, помимо самой функции, и ее производные  стандартным приемом сводится к соответствующей задаче вида (1), (2). В случае обыкновенных дифференциальных уравнений 1-го порядка, не разрешимых относительно производной искомой функции, постановка К. з.- та же, разве что в большей степени опирается на ее геометрич. трактовку, но исследование может осложняться невозможностью (даже локальной) редукции уравнения к нормальной форме (1). Если для обыкновенного дифференциального уравнения постановка и исследование К. з. не содержит принципиальных затруднений, то в случае дифференциальных уравнений с частными производными положение (и, в частности, ответы на вопросы 1) - 4)) существенно усложняется, даже если рассматриваемые функции достаточно регулярны. Это в значительной мере обусловлено многомерностъю пространства независимых переменных и вытекающими из этого (алгебраическими) вопросами разрешимости. Так, условие разрешимости К. з. (в нек-ром смысле промежуточной между "обыкновенностью" и "частностью") для системы уравнений в полных дифференциалах  состоящей в отыскании ( п-k )-мерной интегральной поверхности, проходящей через данную точку, имеет вид  (в окрестности этой точки; здесь d, Для линейных дифференциальных уравнений с частными производными  К. з. ставится следующим образом. В нек-рой области Gпеременных х=( х 1,. . . , х п). найти решение, удовлетворяющее начальным условиям, т, е, принимающее вместе со своими производными до (та-1)-го порядка включительно заданные значения на нек-рой расположенной в G (n-1)-мерной гиперповерхности S(носители начальных условий). Начальные условия можно задавать в виде производных от ипо направлению единичной нормали v к S: 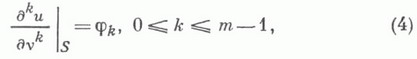 где  Поверхность Sназ. нехарактеристической в точке х 0, если  В этом случае вблизи точки х 0 уравнений (3) можно записать в так наз. нормальной форме  К. з. обычно рассматривается, когда носителем начальных данных является характеристич. поверхность, т. е. когда условие (5) выполнено для всех В теории К. з. важное место занимает Коши - Ковалевской теорема:если S - аналитич. поверхность в окрестности своей точки х 0, функции Для дифференциальных уравнений с частными производными порядка выше 1-го К. з. может оказаться некорректной, если в условиях теоремы Коши - Ковалевской отказаться от аналитичности уравнения или данных Коши. Иллюстрацией служит пример А д а м а р а: К. з. для уравнения Лапласа 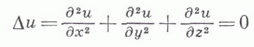 с начальными условиями  не имеет решения, если функция Широкий класс уравнений, для к-рых К. з. поставлена корректно, составляют гиперболич. уравнения. В этом случае К. з. носит глобальный характер, однако условия нехарактеристичности Sпри этом недостаточно. Необходимо, чтобы Sбыла поверхностью пространственного типа. Модельным уравнением гиперболич. типа является волновое уравнение  рассматриваемое в ( п+1)-мерной области переменных ( х, t)=(x1, ..., х n, t). К. з. для этого уравнения с данными 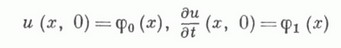 на гиперплоскости t=0 однозначно разрешима для любых достаточно гладких функций  где Множество точек на плоскости t=0, данные Коши на к-ром вполне определяют значение и( х, t).решения волнового уравнения (7) в точке ( х, t), наз. областью зависимости для этой точки. Областями зависимости точки ( х, t).в случаях n=1, n=2 и n=3 являются отрезок, круг и шар, определяемые соотношением Множество точек Эти результаты распространяются на более общий случай, когда носителем данных Коши является: поверхность Sпространственного типа, то есть поверхность, для к-рой величина Qв (5) сохраняет на Sположительное значение. Кроме К. з., для гиперболич. уравнений корректно поставлены и другие задачи, напр. Коши характеристическая задача, смешанная начально-краевая задача; в последней задаче решение имеется в (n+1)-мерном цилиндре с образующей, параллельной оси t, и с основанием S, представляющем собой нек-рую область в пространстве переменных x=(x1, . . ., х п).с границей Г. Носителем начальных условий служит S, а на боковой поверхности Гx{t>0} цилиндра задается значение функции или ее нормальной производной (в случае уравнений 2-го порядка) или более общие краевые условия. Для вырождающихся уравнений К. з. имеет свои особенности. Напр., если уравнение гиперболич. типа и носителем данных Коши является поверхность, на к-рой уравнение параболически вырождается, то в зависимости от характера вырождения принятие начальных условий может осуществляться с нек-рым весом. Лит.:[1] К о в а л е в с к а я С. В., Научные работы, М., 1948; [2] А д а м а р Ж., Задача Коши для линейных уравнений с частными производными гиперболического типа, пер. с франц., М., 1978; [3] Берс Л., Джон Ф.,Шехтер М., Уравнения с частными производными, пер. с англ., М., 1966; [4] Б и ц а д з е А. В., Уравнения математической физики, М., 1976; [5] Курант Р., Уравнения с частными производными, иер. с англ., М., 1964; [6] Мизохата С., Теория уравнений с частными производными, пер. с япон., М., 1977; [7] Тихонов А. Н., Самарский А. А., Уравнения математической физики, 4 изд., М., 1972; [8] Хёрмандер Д., Линейные дифференциальные операторы с частными производными, пер. с англ., М., 1965. А. П. Солдатов. |
|
|
|

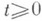 ). От краевых задач К. з. отличается тем, что область, в к-рой должно быть определено искомое решение, здесь заранее не указывается. Тем не менее и К. з. можно рассматривать как одну из краевых задач.
). От краевых задач К. з. отличается тем, что область, в к-рой должно быть определено искомое решение, здесь заранее не указывается. Тем не менее и К. з. можно рассматривать как одну из краевых задач.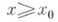 функцию и(х), к-рая удовлетворяет обыкновенному дифференциальному уравнению 1-го порядка
функцию и(х), к-рая удовлетворяет обыкновенному дифференциальному уравнению 1-го порядка 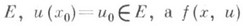 - функция, определенная в
- функция, определенная в  Для существования, единственности и корректности решения К. з. и здесь достаточны условия Пикара.
Для существования, единственности и корректности решения К. з. и здесь достаточны условия Пикара.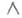 - символы внешнего дифференциала и внешнего произведения соответственно) (см. Фробениуса теорема).
- символы внешнего дифференциала и внешнего произведения соответственно) (см. Фробениуса теорема). - известные функции (данные К о ш и). Аналогичным образом ставится К. з. и для нелинейных дифференциальных уравнений. С К. з. связано понятие нехарактеристич. поверхности. Если неособое преобразование переменных
- известные функции (данные К о ш и). Аналогичным образом ставится К. з. и для нелинейных дифференциальных уравнений. С К. з. связано понятие нехарактеристич. поверхности. Если неособое преобразование переменных  " выпрямляет" поверхность Sв окрестности точки х 0, переводя ее в участок гиперплоскости
" выпрямляет" поверхность Sв окрестности точки х 0, переводя ее в участок гиперплоскости  то в преобразованном уравнении (3) коэффициент при
то в преобразованном уравнении (3) коэффициент при  пропорционален величине
пропорционален величине 
 аналитичны в этой окрестности и выполнено условие (5), то в окрестности точки существует аналитич. решение и(х).К. з. (3), (4), к-рое в классе аналитич. функций единственно. В предположении аналитичности эта теорема справедлива и для общих нелинейных уравнений, если они могут быть приведены к нормальной форме (6), а также для систем таких уравнений. Эта теорема носит универсальный характер, поскольку она применима аналитич. уравнениям независимо от их типа (эллиптического, гиперболического и т. д.) и дает существование решения в малом. Решение единственно в классе неаналитич. функций.
аналитичны в этой окрестности и выполнено условие (5), то в окрестности точки существует аналитич. решение и(х).К. з. (3), (4), к-рое в классе аналитич. функций единственно. В предположении аналитичности эта теорема справедлива и для общих нелинейных уравнений, если они могут быть приведены к нормальной форме (6), а также для систем таких уравнений. Эта теорема носит универсальный характер, поскольку она применима аналитич. уравнениям независимо от их типа (эллиптического, гиперболического и т. д.) и дает существование решения в малом. Решение единственно в классе неаналитич. функций.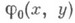 не является аналитической.
не является аналитической. и решение непрерывно зависит в метрике пространств Ck от этих функций. Для случаев n=1, n=2 и n=3 явный вид этого решения дается формулами Д'А л а м б е р а, Пуассона и Кирхгофа соответственно:
и решение непрерывно зависит в метрике пространств Ck от этих функций. Для случаев n=1, n=2 и n=3 явный вид этого решения дается формулами Д'А л а м б е р а, Пуассона и Кирхгофа соответственно: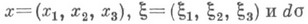 - элемент поверхности единичной сферы
- элемент поверхности единичной сферы 
 (в соответствующем пространстве Rn). Если носителем данных Коши является нек-рая область Sгиперплоскости t=0, то данные Коши в этой области влияют на решение во всех точках ( х, t).множества, для к-рого пересечение
(в соответствующем пространстве Rn). Если носителем данных Коши является нек-рая область Sгиперплоскости t=0, то данные Коши в этой области влияют на решение во всех точках ( х, t).множества, для к-рого пересечение 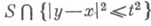 не пусто; это множество наз. областью влияния.
не пусто; это множество наз. областью влияния. , на к-ром решение ивполне определяется по данным Коши на S, наз. областью определения и( х, t) с начальными данными на S. В случае n=1, n=2 и n=3 область определения образуют все точки ( х, t), для к-рых отрезок, круг и шар
, на к-ром решение ивполне определяется по данным Коши на S, наз. областью определения и( х, t) с начальными данными на S. В случае n=1, n=2 и n=3 область определения образуют все точки ( х, t), для к-рых отрезок, круг и шар 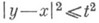 соответственно расположены в S.
соответственно расположены в S.