|
"
0
C
F
G
H
K
L
N
P
S
T
W
Z
А
Б
В
Г
Д
Е
Ж
З
И
Й
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Ш
Э
Ю
Я
КОНФОРМНО-ДИФФЕРЕНЦИАЛЬНАЯ ГЕОМЕТРИЯЗначение КОНФОРМНО-ДИФФЕРЕНЦИАЛЬНАЯ ГЕОМЕТРИЯ в математической энциклопедии: - раздел конформной геометрии, в котором геометрические образы, инвариантные при конформных преобразованиях, изучаются методами анализа бесконечно малых, в первую очередь дифференциального исчисления. В конформной плоскости M2 каждая точка и круг определяются вектором x(x1, х 2, х 3, x4), где х;,i=1,2, 3,4 - тетрациклические координаты. Для точки
для круга (xx)>0. К.-д. г. плоскости изучает последовательности и конгруэнции кругов. Последовательности кругов соответствует в трехмерном гиперболич. пространстве кривая, конгруэнции кругов - поверхность. Последовательность задается параметрич. уравнением x=x(t). Параметр tможно специализировать, взяв в качестве него
da- угол между двумя бесконечно близкими кругами последовательности. Особое значение в теории последовательностей имеют две ветви огибающей этой последовательности v=v(t)и
Можно получить два инварианта b=-2cc и g=c'/c. Инвариант bвыражается через угол j между соприкаcающимися кругами огибающей: b=l/sin2j/2. Теория кривых конформной плоскости строится на основе теории последовательности кругов: каждая кривая рассматривается как огибающая: последовательности, у к-рой инвариант В трехмерном конформном пространстве М 3 уравнение x=х(t)задает последовательность сфер. При ее изучении важную роль играет ее огибающая поверхность, так наз. каналовая поверхность. Каждая последовательность сфер характеризуется тремя инвариантами, выражающимися через нек-рые углы, связанные со сферами последовательности. Конгруэнция кругов в М 2 задается уравнением x=х( и 1, и 2). На поверхности, соответствующей ей в пшерболич. пространстве, удобно ввести полярную нормализацию, приняв за нормаль 1-го рода прямую, ортогональную касательной плоскости поверхности в точке х, а за нормаль 2-го рода- поляру нормали 1 рода относительно абсолюта К(см. [3]). В М 3 нормализации поверхности соответствует нормализация конгруэнции: каждому кругу x. конгруэнции ставится в соответствие круг x. ортогональный кругу x. и всякому бесконечно близкому кругу, и два круга yi, определяющие пучок кругов, сопряженный пучку В теории поверхностей М 3 вводится оснащение поверхности с помощью нормализующих кругов, ортогональных в каждой точке всем касательным сферам поверхности; связывается с каждой точкой конформный репер, состоящий из точки поверхности х, двух координатных сфер уi,i=l, 2, определяющих нормализующий круг, касательной в точке ос сферы zи точки X' пересечения этой сферы и нормализующего круга. В общей теории нормализации поверхностей используется изоморфизм теории нормализованных поверхностей конформного пространства и теории внутренних полярных нормализации абсолюта гиперболпч. пространства. Внутренняя геометрия нормализованной поверхности М п есть геометрия Вейля, основной тензор к-рой совпадает с тензором угловой метрики поверхности, а дополнительный тензор есть нормализатор, определяющий опорные координатные сферы. Результаты, полученные для нормализованной поверхности, справедливы и для нормализованного конформного пространства. Лит.:[1] Dаrbоuх G., Lecons sur la theorie generale des surfaus, pt. 1-4, P., 1887-96; 2 "d., pt. 1- 2, P., 1914 - 26: [2] Вlasсhk e W., Vorlesungen uber Differentialgeometrie, Bd 3, В., 1929; [3] Норией А. П., Пространства аффинной связности, 2 изд., М.. 1976; [4] Бушманова Г. В., Норден А. П., Элементы конформной геометрии, Казань, 1972. Г. В. Бушманова. |
|
|
|



 их соприкасающиеся круги. Как и в обычной дифференциальной геометрии кривых можно записать деривационные формулы для последовательности кругов, разложив производные векторов x,
их соприкасающиеся круги. Как и в обычной дифференциальной геометрии кривых можно записать деривационные формулы для последовательности кругов, разложив производные векторов x, по ним самим:
по ним самим: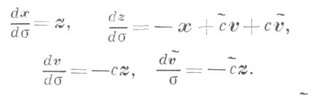
 Если при этом инвариант bпостоянный, то кривая оказывается изогональной траекторией пучка кругов, т. е. локсодромой.
Если при этом инвариант bпостоянный, то кривая оказывается изогональной траекторией пучка кругов, т. е. локсодромой. В соответствии с инвариантами поверхности в пшерболич. пространстве на М 2 определяются инварианты конгруэнции кругов, выделяются специальные виды конгруэнции.
В соответствии с инвариантами поверхности в пшерболич. пространстве на М 2 определяются инварианты конгруэнции кругов, выделяются специальные виды конгруэнции.