|
"
0
C
F
G
H
K
L
N
P
S
T
W
Z
А
Б
В
Г
Д
Е
Ж
З
И
Й
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Ш
Э
Ю
Я
КОНСТРУКТИВНОЕ ПОДМНОЖЕСТВОЗначение КОНСТРУКТИВНОЕ ПОДМНОЖЕСТВО в математической энциклопедии: алгебраического многообразия - конечное объединение локально замкнутых (в Зариского топологии )подмножеств. Локально замкнутым подмножеством наз. пересечение открытого и замкнутого подмножеств. К. п. образуют булеву алгебру и могут быть определены как элементы булевой алгебры, порожденной алгебраич. подмногообразиями. Роль К. п. в алгебраич. геометрии объясняет следующая теорема ГОевалле: если Отображение h: Лит.:[1] Grothendieck A., Elements de geometrie algebrique, t. 4, P., 1964; [2] Борель А., Линейные алгебраические группы, пер. с англ., М., 1972. В. И. Данилов. |
|
|
|
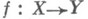- морфизм алгебраич. многообразий, то f(X)(и более того, образ любого К. п. из X)является К. п. в У. С этим фактом связано то, что "алгебраические" условия выделяют конструктивные подмножества алгебраич. многообразий.
наз. конструктивным, если h{X )конечно и для любой точки 
прообраз A-1(i) есть К. п. в X.