"
0
C
F
G
H
K
L
N
P
S
T
W
Z
А
Б
В
Г
Д
Е
Ж
З
И
Й
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Ш
Э
Ю
Я
КОНСТРУКТИВНАЯ СЕМАНТИКА
Значение КОНСТРУКТИВНАЯ СЕМАНТИКА в математической энциклопедии:
- совокупность способов понимания суждений в конструктивной математике. Необходимость в особой семантике вызвана различием общих принципов, лежащих в основе традиционной (классической) и конструктивной математики (далее последний термин будет в основном относиться к подходу, развитому в советской школе конструктивной математики). Основное внимание К. с. уделяет суждениям о конструктивных объектах в языках первого порядка, то есть, по существу, арифметич. суждениям (см. Арифметика формальная). Принципиальные различия с традиционной семантикой в понимании дизъюнкций  (и суждений о существовании
(и суждений о существовании  сформулированы Л. Брауэром (L. Brouwer). Конструктивное обоснование таких суждений требует решения задачи: найти число
сформулированы Л. Брауэром (L. Brouwer). Конструктивное обоснование таких суждений требует решения задачи: найти число 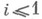 такое, что верно Ai (соответственно найти число птакое, что А(n)). Общие принципы описания задач, соответствующих более сложным формулам, были намечены А. Рейтингом (А. Неуting) и А. Н. Колмогоровым. Точная формулировка (к-рая стала возможной после появления магематич. определения алгоритма). была дана С. Клини (S. Kleene) в виде понятия реализации замкнутой арифметич. формулы (см. Рекурсивная реализуемость). Реализация верного равенства t=r есть фиксированная константа, напр, число 0, а ложное равенство не имеет реализаций. Реализация конъюнкции АaВ- это пара (а, b), где а- реализация А, b- реализация В. Реализация дизъюнкции
такое, что верно Ai (соответственно найти число птакое, что А(n)). Общие принципы описания задач, соответствующих более сложным формулам, были намечены А. Рейтингом (А. Неуting) и А. Н. Колмогоровым. Точная формулировка (к-рая стала возможной после появления магематич. определения алгоритма). была дана С. Клини (S. Kleene) в виде понятия реализации замкнутой арифметич. формулы (см. Рекурсивная реализуемость). Реализация верного равенства t=r есть фиксированная константа, напр, число 0, а ложное равенство не имеет реализаций. Реализация конъюнкции АaВ- это пара (а, b), где а- реализация А, b- реализация В. Реализация дизъюнкции  - это пара (i, а), где i=0,1 на - реализация суждения А i. Реализация суждения
- это пара (i, а), где i=0,1 на - реализация суждения А i. Реализация суждения  - это пара {п, а), где п- число, а- реализация суждения (п). Реализация суждения
- это пара {п, а), где п- число, а- реализация суждения (п). Реализация суждения  - это общий метод f, к-рый по всякому натуральному пвыдает реализацию f(n)суждения А(n). Реализация суждения
- это общий метод f, к-рый по всякому натуральному пвыдает реализацию f(n)суждения А(n). Реализация суждения  - это общий метод f, к-рый по всякой реализации асуждения А выдает реализацию f(a)суждения В(и может быть не определен для аргументов а, не являющихся реализациями А). При этом общий метод понимается как алгоритм (частично рекурсивная функция). Используя кодирование алгоритмов числами, можно записать условие "число еесть реализация формулы Л" в виде арифметич. формулы ( еrА), не содержащей дизъюнкции
- это общий метод f, к-рый по всякой реализации асуждения А выдает реализацию f(a)суждения В(и может быть не определен для аргументов а, не являющихся реализациями А). При этом общий метод понимается как алгоритм (частично рекурсивная функция). Используя кодирование алгоритмов числами, можно записать условие "число еесть реализация формулы Л" в виде арифметич. формулы ( еrА), не содержащей дизъюнкции  и содержащей существование
и содержащей существование  только тривиальным образом - перед равенствами. Такие формулы наз. почти нормальными. Суждение
только тривиальным образом - перед равенствами. Такие формулы наз. почти нормальными. Суждение  (читаемое "А реализуема") может служить конструктивным разъяснением суждения А. При таком понимании закон исключенного третьего
(читаемое "А реализуема") может служить конструктивным разъяснением суждения А. При таком понимании закон исключенного третьего  х (А(х)
х (А(х) опровергается, напр., для
опровергается, напр., для  где Т( е, х, у )означает, что алгоритм (с кодом) езаканчивает работу над аргументом хза ушагов. Опровергается и закон двойного отрицания
где Т( е, х, у )означает, что алгоритм (с кодом) езаканчивает работу над аргументом хза ушагов. Опровергается и закон двойного отрицания  В(х)), напр, для
В(х)), напр, для  Приведенное определение связывает конструктивную задачу (поиск реализации) со всяким суждением А, даже если Ане содержит
Приведенное определение связывает конструктивную задачу (поиск реализации) со всяким суждением А, даже если Ане содержит  Предложенный Н. А. Шаниным алгоритм выявления конструктивной задачи не"меняет формул без
Предложенный Н. А. Шаниным алгоритм выявления конструктивной задачи не"меняет формул без  (нормальных формул) и эквивалентен реализуемости в формальной интуиционистской арифметике с бескванторной индукцией. Произвольные формулы сводятся к почти нормальным, так как обоснование
(нормальных формул) и эквивалентен реализуемости в формальной интуиционистской арифметике с бескванторной индукцией. Произвольные формулы сводятся к почти нормальным, так как обоснование  состоит в предъявлении числа пи обосновании (п). К. с. для почти нормальных формул определяется разными авторами по-разному, однако ни в одном случае не получается столь существенного расхождения с классическим пониманием, как для формул, содержащих
состоит в предъявлении числа пи обосновании (п). К. с. для почти нормальных формул определяется разными авторами по-разному, однако ни в одном случае не получается столь существенного расхождения с классическим пониманием, как для формул, содержащих  п нетривиальное
п нетривиальное 
А. А. Марков определяет истинность для почти нормальных формул с помощью выводимости по обычным правилам для рассматриваемых логических связок плюс эффективное w-правило: если имеется общий метод, позволяющий для любого пустанавливать выводимость А(n) из суждения К, то  выводимо из А". Истинность определяется постепенно. Язык Я w, состоящий из всех почти нормальных формул, делится на слон Я 1, Я 2, ... ; язык Я 1 состоит из формул без
выводимо из А". Истинность определяется постепенно. Язык Я w, состоящий из всех почти нормальных формул, делится на слон Я 1, Я 2, ... ; язык Я 1 состоит из формул без 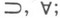 язык Я п+1,
язык Я п+1, включает Я п и формулы, к-рые можно построить из формул языка Я n одним применением импликации и любым числом применений
включает Я п и формулы, к-рые можно построить из формул языка Я n одним применением импликации и любым числом применений  a. Истинность для Я 1 -формул - это выводимость по обычным правилам для a,
a. Истинность для Я 1 -формул - это выводимость по обычным правилам для a,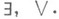 Истинность для Я 2 -формул определяется через допустимость соответствующего правила. Напр., истинность
Истинность для Я 2 -формул определяется через допустимость соответствующего правила. Напр., истинность  означает наличие алгоритма j такого, что
означает наличие алгоритма j такого, что  для любого числа п. Для Я n+1 формул при n>1 истинность конъюнкций и v-формул определяется обычным образом через истинность компонент, а истинность импликации
для любого числа п. Для Я n+1 формул при n>1 истинность конъюнкций и v-формул определяется обычным образом через истинность компонент, а истинность импликации 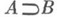 означает выводимость B из A по нек-рым правилам Sn, о к-рых уже доказано, что они сохраняют истинность Я n -формул. Системы Sn содержат w-правило, а в качестве аксиом - все истинные Я n -формулы. Понятие выводимости в Sn вводится обобщенным индуктивным определением, а для доказательства метатеорем применяется соответствующий принцип индукции. Индукцией по S2 -выводу доказывается допустимость правила
означает выводимость B из A по нек-рым правилам Sn, о к-рых уже доказано, что они сохраняют истинность Я n -формул. Системы Sn содержат w-правило, а в качестве аксиом - все истинные Я n -формулы. Понятие выводимости в Sn вводится обобщенным индуктивным определением, а для доказательства метатеорем применяется соответствующий принцип индукции. Индукцией по S2 -выводу доказывается допустимость правила  Оно включается в S3 и дает принцип Маркова
Оно включается в S3 и дает принцип Маркова  Системы Sn+3,
Системы Sn+3, состоят из обычных правил для рассматриваемых связок, включая w-правило. Оказывается, что почти нормальная формула Аистинна по Маркову тогда и только тогда, когда примитивно рекурсивное дерево TA поиска вывода формулы Абез сечения (но с w-правилом и принципом Маркова) является выводом в смысле индуктивного определения. Это эквивалентно (в рамках классической математики) классической истинности А. В мажорантной семантике Н. А. Шанина для каждой почти нормальной формулы Аопределяется трансфинитная иерархия {Аa} формул простой структуры, причем
состоят из обычных правил для рассматриваемых связок, включая w-правило. Оказывается, что почти нормальная формула Аистинна по Маркову тогда и только тогда, когда примитивно рекурсивное дерево TA поиска вывода формулы Абез сечения (но с w-правилом и принципом Маркова) является выводом в смысле индуктивного определения. Это эквивалентно (в рамках классической математики) классической истинности А. В мажорантной семантике Н. А. Шанина для каждой почти нормальной формулы Аопределяется трансфинитная иерархия {Аa} формул простой структуры, причем  доказуемо в подходящей формальной системе. Формула А a. наз. мажорантой для А, и А считается истинной формулой ранга а, если А a. верна. Точность аппроксимации растет с ростом а:
доказуемо в подходящей формальной системе. Формула А a. наз. мажорантой для А, и А считается истинной формулой ранга а, если А a. верна. Точность аппроксимации растет с ростом а: Ab). Если отвлечься от технических деталей, то формула Астроится с помощью a-кратного вынесения кванторов, согласно эквивалентности
Ab). Если отвлечься от технических деталей, то формула Астроится с помощью a-кратного вынесения кванторов, согласно эквивалентности

и сворачивания цепочек кванторов с помощью алгоритма выявления конструктивной задачи. Это дает доказуемую в арифметике с трансфинитной индукцией до а эквивалентность

с бескванторной формулой С a, так что
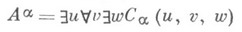
оказывается мажорантой для А. Суждение А a оказывается, с точностью до технических деталей, эквивалентным утверждению о существовании вывода высоты <a для исходной формулы с использованием w-правила. В этом смысле мажорантная семантика эквивалентна ступенчатой семантике А. А. Маркова. После фиксации нек-рого класса в общерекурсивных функций (напр., класса всех функций, определимых рекурсией до а) определяются мажоранты еще более простой структуры:

Если К- бескванторное исчисление для класса в, то K-истинность формулы Eu"vC(u, v )определяется как выводимость формулы С(t, v )с переменной vдля нек-рого постоянного терма t. Если в качестве Квзято стандартное исчисление равенств для функций, определимых рекурсией до ординалов, меньших a, то K-истинными оказываются формулы, выводимые в формальной интуиционистской арифметике, пополненной принципом Маркова, соотношениями, определяющими алгоритм выявления конструктивной задачи, и правилом индукции до ординалов b таких, что  где e(b) - первое е-число, большее р. В частности, a=e0 для b=w, т. е. для обычной индукции.
где e(b) - первое е-число, большее р. В частности, a=e0 для b=w, т. е. для обычной индукции.
Доведение обоснования до бескванторного уровня (К-истинность) связано со стремлением остаться по возможности в рамках финитизма, т. е. бескванторного языка и соответствующих логических средств. С этим же связано стремление ограничиться небольшими a. Для большей части "работающего" конструктивного анализа (включая теорему о непрерывности эффективных операторов) достаточно конечных a.
Лит.:[1] Марков А. А., в сб.: Исследования по теории алгорифмов и математической логике, М., 1976, т. 2, с.3-31; [2] Шанин Н. А., "Тр. Матем. ин-та АН СССР", 1973, т. 129, с. 203-66; [3] Клини С. К., Введение в метаматематику, пер. с англ., М., 1957. Г. Е. Минц.

 (и суждений о существовании
(и суждений о существовании  сформулированы Л. Брауэром (L. Brouwer). Конструктивное обоснование таких суждений требует решения задачи: найти число
сформулированы Л. Брауэром (L. Brouwer). Конструктивное обоснование таких суждений требует решения задачи: найти число 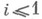 такое, что верно Ai (соответственно найти число птакое, что А(n)). Общие принципы описания задач, соответствующих более сложным формулам, были намечены А. Рейтингом (А. Неуting) и А. Н. Колмогоровым. Точная формулировка (к-рая стала возможной после появления магематич. определения алгоритма). была дана С. Клини (S. Kleene) в виде понятия реализации замкнутой арифметич. формулы (см. Рекурсивная реализуемость). Реализация верного равенства t=r есть фиксированная константа, напр, число 0, а ложное равенство не имеет реализаций. Реализация конъюнкции АaВ- это пара (а, b), где а- реализация А, b- реализация В. Реализация дизъюнкции
такое, что верно Ai (соответственно найти число птакое, что А(n)). Общие принципы описания задач, соответствующих более сложным формулам, были намечены А. Рейтингом (А. Неуting) и А. Н. Колмогоровым. Точная формулировка (к-рая стала возможной после появления магематич. определения алгоритма). была дана С. Клини (S. Kleene) в виде понятия реализации замкнутой арифметич. формулы (см. Рекурсивная реализуемость). Реализация верного равенства t=r есть фиксированная константа, напр, число 0, а ложное равенство не имеет реализаций. Реализация конъюнкции АaВ- это пара (а, b), где а- реализация А, b- реализация В. Реализация дизъюнкции  - это пара (i, а), где i=0,1 на - реализация суждения А i. Реализация суждения
- это пара (i, а), где i=0,1 на - реализация суждения А i. Реализация суждения  - это пара {п, а), где п- число, а- реализация суждения (п). Реализация суждения
- это пара {п, а), где п- число, а- реализация суждения (п). Реализация суждения  - это общий метод f, к-рый по всякому натуральному пвыдает реализацию f(n)суждения А(n). Реализация суждения
- это общий метод f, к-рый по всякому натуральному пвыдает реализацию f(n)суждения А(n). Реализация суждения  - это общий метод f, к-рый по всякой реализации асуждения А выдает реализацию f(a)суждения В(и может быть не определен для аргументов а, не являющихся реализациями А). При этом общий метод понимается как алгоритм (частично рекурсивная функция). Используя кодирование алгоритмов числами, можно записать условие "число еесть реализация формулы Л" в виде арифметич. формулы ( еrА), не содержащей дизъюнкции
- это общий метод f, к-рый по всякой реализации асуждения А выдает реализацию f(a)суждения В(и может быть не определен для аргументов а, не являющихся реализациями А). При этом общий метод понимается как алгоритм (частично рекурсивная функция). Используя кодирование алгоритмов числами, можно записать условие "число еесть реализация формулы Л" в виде арифметич. формулы ( еrА), не содержащей дизъюнкции  и содержащей существование
и содержащей существование  только тривиальным образом - перед равенствами. Такие формулы наз. почти нормальными. Суждение
только тривиальным образом - перед равенствами. Такие формулы наз. почти нормальными. Суждение  (читаемое "А реализуема") может служить конструктивным разъяснением суждения А. При таком понимании закон исключенного третьего
(читаемое "А реализуема") может служить конструктивным разъяснением суждения А. При таком понимании закон исключенного третьего  х (А(х)
х (А(х) опровергается, напр., для
опровергается, напр., для  где Т( е, х, у )означает, что алгоритм (с кодом) езаканчивает работу над аргументом хза ушагов. Опровергается и закон двойного отрицания
где Т( е, х, у )означает, что алгоритм (с кодом) езаканчивает работу над аргументом хза ушагов. Опровергается и закон двойного отрицания  В(х)), напр, для
В(х)), напр, для  Приведенное определение связывает конструктивную задачу (поиск реализации) со всяким суждением А, даже если Ане содержит
Приведенное определение связывает конструктивную задачу (поиск реализации) со всяким суждением А, даже если Ане содержит  Предложенный Н. А. Шаниным алгоритм выявления конструктивной задачи не"меняет формул без
Предложенный Н. А. Шаниным алгоритм выявления конструктивной задачи не"меняет формул без  (нормальных формул) и эквивалентен реализуемости в формальной интуиционистской арифметике с бескванторной индукцией. Произвольные формулы сводятся к почти нормальным, так как обоснование
(нормальных формул) и эквивалентен реализуемости в формальной интуиционистской арифметике с бескванторной индукцией. Произвольные формулы сводятся к почти нормальным, так как обоснование  состоит в предъявлении числа пи обосновании (п). К. с. для почти нормальных формул определяется разными авторами по-разному, однако ни в одном случае не получается столь существенного расхождения с классическим пониманием, как для формул, содержащих
состоит в предъявлении числа пи обосновании (п). К. с. для почти нормальных формул определяется разными авторами по-разному, однако ни в одном случае не получается столь существенного расхождения с классическим пониманием, как для формул, содержащих  п нетривиальное
п нетривиальное 
 выводимо из А". Истинность определяется постепенно. Язык Я w, состоящий из всех почти нормальных формул, делится на слон Я 1, Я 2, ... ; язык Я 1 состоит из формул без
выводимо из А". Истинность определяется постепенно. Язык Я w, состоящий из всех почти нормальных формул, делится на слон Я 1, Я 2, ... ; язык Я 1 состоит из формул без 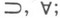 язык Я п+1,
язык Я п+1, включает Я п и формулы, к-рые можно построить из формул языка Я n одним применением импликации и любым числом применений
включает Я п и формулы, к-рые можно построить из формул языка Я n одним применением импликации и любым числом применений  a. Истинность для Я 1 -формул - это выводимость по обычным правилам для a,
a. Истинность для Я 1 -формул - это выводимость по обычным правилам для a,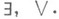 Истинность для Я 2 -формул определяется через допустимость соответствующего правила. Напр., истинность
Истинность для Я 2 -формул определяется через допустимость соответствующего правила. Напр., истинность  означает наличие алгоритма j такого, что
означает наличие алгоритма j такого, что  для любого числа п. Для Я n+1 формул при n>1 истинность конъюнкций и v-формул определяется обычным образом через истинность компонент, а истинность импликации
для любого числа п. Для Я n+1 формул при n>1 истинность конъюнкций и v-формул определяется обычным образом через истинность компонент, а истинность импликации 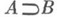 означает выводимость B из A по нек-рым правилам Sn, о к-рых уже доказано, что они сохраняют истинность Я n -формул. Системы Sn содержат w-правило, а в качестве аксиом - все истинные Я n -формулы. Понятие выводимости в Sn вводится обобщенным индуктивным определением, а для доказательства метатеорем применяется соответствующий принцип индукции. Индукцией по S2 -выводу доказывается допустимость правила
означает выводимость B из A по нек-рым правилам Sn, о к-рых уже доказано, что они сохраняют истинность Я n -формул. Системы Sn содержат w-правило, а в качестве аксиом - все истинные Я n -формулы. Понятие выводимости в Sn вводится обобщенным индуктивным определением, а для доказательства метатеорем применяется соответствующий принцип индукции. Индукцией по S2 -выводу доказывается допустимость правила  Оно включается в S3 и дает принцип Маркова
Оно включается в S3 и дает принцип Маркова  Системы Sn+3,
Системы Sn+3, состоят из обычных правил для рассматриваемых связок, включая w-правило. Оказывается, что почти нормальная формула Аистинна по Маркову тогда и только тогда, когда примитивно рекурсивное дерево TA поиска вывода формулы Абез сечения (но с w-правилом и принципом Маркова) является выводом в смысле индуктивного определения. Это эквивалентно (в рамках классической математики) классической истинности А. В мажорантной семантике Н. А. Шанина для каждой почти нормальной формулы Аопределяется трансфинитная иерархия {Аa} формул простой структуры, причем
состоят из обычных правил для рассматриваемых связок, включая w-правило. Оказывается, что почти нормальная формула Аистинна по Маркову тогда и только тогда, когда примитивно рекурсивное дерево TA поиска вывода формулы Абез сечения (но с w-правилом и принципом Маркова) является выводом в смысле индуктивного определения. Это эквивалентно (в рамках классической математики) классической истинности А. В мажорантной семантике Н. А. Шанина для каждой почти нормальной формулы Аопределяется трансфинитная иерархия {Аa} формул простой структуры, причем  доказуемо в подходящей формальной системе. Формула А a. наз. мажорантой для А, и А считается истинной формулой ранга а, если А a. верна. Точность аппроксимации растет с ростом а:
доказуемо в подходящей формальной системе. Формула А a. наз. мажорантой для А, и А считается истинной формулой ранга а, если А a. верна. Точность аппроксимации растет с ростом а: Ab). Если отвлечься от технических деталей, то формула Астроится с помощью a-кратного вынесения кванторов, согласно эквивалентности
Ab). Если отвлечься от технических деталей, то формула Астроится с помощью a-кратного вынесения кванторов, согласно эквивалентности

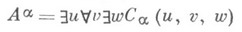

 где e(b) - первое е-число, большее р. В частности, a=e0 для b=w, т. е. для обычной индукции.
где e(b) - первое е-число, большее р. В частности, a=e0 для b=w, т. е. для обычной индукции.