|
"
0
C
F
G
H
K
L
N
P
S
T
W
Z
А
Б
В
Г
Д
Е
Ж
З
И
Й
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Ш
Э
Ю
Я
КОНДУКТОРЗначение КОНДУКТОР в математической энциклопедии: характера - целое число, сопоставляемое характеру нек-рого представления группы Галуа конечного расширения локальных полей. Пусть К- полное поле дискретного нормирования с полем вычетов kхарактеристики
где причем П обозначает простой элемент поля L,a vL - соответствующее нормирование. Для ( п, p)=i будет G0=G, Gi-={1} для i>0 и f(c)=c(i)-c(Gi). Если c.- характер рационального представления М, то c(Gi)= числом, равным 0 только, если n=1. Лит.:[1] Алгебраическая теория чисел, пер. с англ., М., 1969; [2] Аrtin E.,Tate J., Class field theory, N. Y.-Amst., 1967; [3] Серр Ж.-П., Абелевы l-адические представления и эллиптические кривые, пер. с англ., М., 1973. И. В. Долгачев. |
|
|
|
L/K- его расширение Галуа степени пс группой Галуа G. Если c.- характер некоторого конечномерного комплексного представления группы G, то его К. f(c) определяется формулой: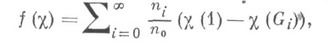
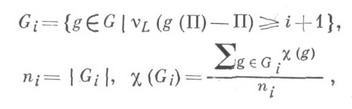
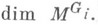К. f(c). является целым положительным