|
"
0
C
F
G
H
K
L
N
P
S
T
W
Z
А
Б
В
Г
Д
Е
Ж
З
И
Й
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Ш
Э
Ю
Я
КОМПЛЕКСНОЕ ЧИСЛОЗначение КОМПЛЕКСНОЕ ЧИСЛО в математической энциклопедии: - число вида z=x+iy, где хи у- действительные числа, а Алгебраическая природа К. ч. состоит в том, что К. ч. есть элемент (алгебраического) расширения С поля действительных чисел R, получаемого алгебраич. присоединением к полю R корня iмногочлена Х 2+1. Получающееся таким путем поле С наз. полем комплексных чисел. Наиболее важное свойство поля С состоит в том, что оно алгебраически замкнуто, т. е. любой многочлен с коэффициентами из С разлагается на линейные множители. Иначе это свойство алгебраич. замкнутости выражается в том, что любой многочлен степени Фактическое построение поля С осуществляется следующим образом. В качестве элементов z=(x, у), z' =(x', у'), ..., или комплексных чисел, принимаются точки ( х, у),( х', у'), . . ., плоскости R2 с декартовыми прямоугольными координатами хи у, х' и у', ..., причем суммой К. ч. z=(x, у )и z'=( х', у' )наз. К. ч. ( х+х', у+у'), т. е.
а произведением этих К. ч. наз. К. ч. ( хх'-уу', ху'+х'у), т. е.
Нулевой элемент 0=(0, 0) совпадает с началом координат, К. ч. (1, 0) есть единица поля С. Плоскость R2, точки к-рой отождествлены с элементами поля С, наз. комплексной плоскостью. Действительные числа х, х', ... отождествляются при этом с точками ( х,0), ( х', 0), ... оси абсцисс, к-рая применительно к плоскости С наз. действительной, или вещественной, осью. Точки (0, y)=iy,(0, y')=iy',... располагаются на оси ординат, называемой на комплексной плоскости С мнимой ось ю; числа вида iy, iy',... наз. чисто мнимыми. Это представление элементов z, z', ... поля С, или К. ч., в виде точек комплексной плоскости с правилами действий (1) и (2) равносильно указанной выше наиболее употребительной форме записи К. ч.:
называемой также алгебраической, или декартовой, формой записи К. ч. Применительно к алгебраич. форме правила (1) и (2) сводятся к простому условию, что все действия с К. ч. выполняются как с многочленами с учетом свойства мнимой единицы: i-i=j2=-1. К. ч. z=(x, y) = x+iy и .
где К. ч. z отлично от 0 тогда и только тогда, когда |z|>0. Отображение
Операции сложения и умножения (1) и (2) коммутативны и ассоциативны, связаны соотношением дистрибутивности и для них существуют обратные действия вычитания и деления (кроме деления на нуль), записываемые в алгебраич. форме следующим образом:
Деление К. ч. z' на К. ч.
На важный вопрос о том, является ли построенное расширение С поля действительных чисел с указанными выше правилами действий единственно возможным или же мыслимы существенно иные варианты, дает ответ теорема единственности: всякое (алгебраическое) расширение поля R, получающееся из R присоединением корня iуравнения Х 2+1=0, изоморфно С, т. е. с требованием алгебраич. присоединения корня iсовместимы только указанные выше правила действий с К. ч. Этому факту, однако, не противоречит наличие других интерпретаций К. ч., отличных от истолкования К. ч. как точек комплексной плоскости. Наиболее часто в приложениях используются следующие две интерпретации. Векторная интерпретация. К. ч. z=x+iy можно отождествить с вектором ( х, у )с координатами хн у, приложенным в начале координат (см. рис.). При такой интерпретации сложение и вычитание К. ч. производится по правилам сложения и вычитания векторов. Однако умножение и деление К. ч., совершаемые необходимо по формулам (2) и (3), не имеют непосредственных аналогов в векторной алгебре (см. [4], [5]). Векторная интерпретация К. ч. непосредственно применяется, напр., в электротехнике для изображения переменных синусоидальных токов и напряжений. Матричная интерпретация. К. ч. w=u+iv можно отождествить с матрицей второго порядка специального вида
причем действия сложения, вычитания и умножения выполняются по обычным правилам матричной алгебры. Применяя полярные координаты на комплексной плоскости С, т. <е. радиус-вектор r=|z| и полярный угол j=Arg z, называемый здесь аргументом К. ч. z (иногда также фазой, или амплитудой, К. ч. z), получают тригонометрическую, или полярную, форму К. ч.: z=r(cos j+i sin j), r соs j=Re z, r sin j=Im z. (4)
Аргумент j=Аrg z является многозначной действительной функцией К. ч.
Формы (4) и (5) особенно удобны для выполнения умножения и деления К. ч.:
При умножении (делении) К. ч. модули перемножаются (модуль делимого делится на модуль делителя) а аргументы складываются (из аргумента делимого вычитается аргумент делителя). Возведение в степень К. ч. и извлечение корня из К. ч. производятся по так наз. формулам Муавра:
причем первая из них применима и для целых отрицательных показателей п. Геометрически умножение К. ч. z на К. ч. z' = r'eij' сводится к повороту вектора z на угол ф' (против часовой стрелки при j' >0) и последующему изменению его длины в |z'| = r' раз; в частности, умножение на К. ч. z' = е ij', по модулю равное единице, есть не что иное как поворот на угол j'. Таким образом, К. ч. могут быть истолкованы и как операторы специального вида ( аффиноры). В связи с этим иногда удобна смешанная векторно-матричная интерпретация умножения К. ч.:
при к-рой множимое трактуется как матрица-вектор,. а множитель - как матрица-оператор. Биективное отображение Впервые, по-видимому, мнимые величины появились в известном труде "Великое искусство, или об алгебраических правилах" Дж. Кардано (G. Cardano, 1545), к-рый счел их бесполезными, непригодными к употреблению. Пользу мнимых величин, в частности при решении кубического уравнения в так наз. неприводимом случае (когда действительные корни выражаются через кубические корни из мнимых величин) впервые оценил Р. Бомбелли (В. Bombelli, 1572). Он же дал нек-рые простейшие правила действий с К. ч. Вообще, выражения вида Задача о выражении корней степени п из данного" числа была в основном решена в работах А. Муавра (A. de Moivre, 1707, 1724) и Р. Котеса (R. Cotes, 1722). Символ Чисто арифметич. теория К. ч. как пар действительных чисел была построена У. Гамильтоном (VV. Hamilton, 1837). Ему же принадлежит важное пространственное обобщение К. ч.- кватернионы, алгебра к-рых некоммутативна. Вообще, в конце 19 в. было доказано, что всякое расширение понятия числа за пределы поля К. ч. возможно только при отказе от каких-либо обычных действий (прежде всего коммутативности). См. также Гиперкомплексное число, Двойные и дуальные числа, Кэли число. Лит.:[1] Курош А. Г., Курс высшей алгебры, 9 изд., М., 1968; [2] Кострикин А. И., Введение в алгебру, М., 1977; [31 Маркушевич А. И., Теория аналитических функций, т. 1, 2 изд., М., 1967; [4] Шабат Б. В., Введение в комплексный анализ, ч. 1, 2 изд., М., 1976; [5] Лаврентьев М. А., Шабат Б. В., Проблемы гидродинамики и их математические модели, 2 изд., М., 1977; [6] Гурвиц А., Курант Р., Теория функций, пер. с нем., М., 1968; [7] Харди Г. X., Курс чистой математики, пер. с англ., М., 1949; [8] Бурбаки Н., Общая топология. Топологические труппы. Числа и связанные с ними пространства, пер. с франц., М., 1969. Е. Д. Соломещев. |
|
|
|

 - так наз. мнимая единица, т. е. число, квадрат к-рого равен -1 (в технической литературе применяется также обозначение
- так наз. мнимая единица, т. е. число, квадрат к-рого равен -1 (в технической литературе применяется также обозначение  ); хназ. действительной, или вещественной, частью К. ч. z, а у- его мнимой частью (обозначения x=Re z, y=Im z). Действительные числа - частный случай К. ч. при у=0;К. ч., не являющиеся действительными, т. е. такие, что у неравно 0, иногда наз. мнимым и числами. В приведенных терминах, в основном традиционного происхождения, нашел свое отражение сложный исторический процесс развития понятия К. ч.
); хназ. действительной, или вещественной, частью К. ч. z, а у- его мнимой частью (обозначения x=Re z, y=Im z). Действительные числа - частный случай К. ч. при у=0;К. ч., не являющиеся действительными, т. е. такие, что у неравно 0, иногда наз. мнимым и числами. В приведенных терминах, в основном традиционного происхождения, нашел свое отражение сложный исторический процесс развития понятия К. ч. с коэффициентами из С имеет в С по крайней мере один корень (теорема Д'Аламбера - Гаусса).
с коэффициентами из С имеет в С по крайней мере один корень (теорема Д'Аламбера - Гаусса).


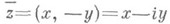 наз. сопряженными, на плоскости С они располагаются симметрично относительно действительной оси. Сумма и произведение сопряженных К. ч. суть действительные числа:
наз. сопряженными, на плоскости С они располагаются симметрично относительно действительной оси. Сумма и произведение сопряженных К. ч. суть действительные числа: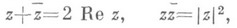
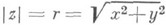 наз. модулем, или абсолютной величиной, К. ч. z. Всегда
наз. модулем, или абсолютной величиной, К. ч. z. Всегда 
 есть автоморфизм комплексной плоскости порядка 2 (т. е.
есть автоморфизм комплексной плоскости порядка 2 (т. е. ), оставляющий на месте все точки действительной оси. При этом
), оставляющий на месте все точки действительной оси. При этом  ,
,

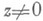 сводится, таким образом, к умножению z' на К. ч.
сводится, таким образом, к умножению z' на К. ч.


 значения к-рой для данного z отличаются одно от другого на целое кратное 2л; аргумент К. ч. z=0 не определен. Обычно используется главное значение аргумента j=arg z, определяемое дополнительным условием
значения к-рой для данного z отличаются одно от другого на целое кратное 2л; аргумент К. ч. z=0 не определен. Обычно используется главное значение аргумента j=arg z, определяемое дополнительным условием  Эйлера формулы
Эйлера формулы преобразуют тригонометрич. форму (4) в показательную форму К. ч.:
преобразуют тригонометрич. форму (4) в показательную форму К. ч.:



 переносит в поле К. ч. С топологию двумерного действительного числового пространства R2, эта топология согласуется со структурой поля С и, таким образом, С есть топологическое тело. Модуль z есть евклидова норма К. ч. z = (z, у), и поле С, наделенное этой нормой, есть комплексное одномерное евклидово пространство, называемое также плоскостью комплексного переменного С. Топологич. произведение С n=
переносит в поле К. ч. С топологию двумерного действительного числового пространства R2, эта топология согласуется со структурой поля С и, таким образом, С есть топологическое тело. Модуль z есть евклидова норма К. ч. z = (z, у), и поле С, наделенное этой нормой, есть комплексное одномерное евклидово пространство, называемое также плоскостью комплексного переменного С. Топологич. произведение С n= ( п раз,
( п раз,  ) есть комплексное n-мерное евклидово пространство. Вследствие алгебраич. замкнутости поля К. ч. С, изучение функций и математич. анализ вообще приобретают должную полноту и законченность только при рассмотрении поведения функций: в комплексной области. В частности, даже поведение таких элементарных функций, как zn,cos z, sin z, ez, может быть правильно понято только при условии их рассмотрения как функций комплексного переменного (см. Аналитическая функция).
) есть комплексное n-мерное евклидово пространство. Вследствие алгебраич. замкнутости поля К. ч. С, изучение функций и математич. анализ вообще приобретают должную полноту и законченность только при рассмотрении поведения функций: в комплексной области. В частности, даже поведение таких элементарных функций, как zn,cos z, sin z, ez, может быть правильно понято только при условии их рассмотрения как функций комплексного переменного (см. Аналитическая функция). появляющиеся при решении квадратных и кубических уравнений, стали называть, в 16 -17 вв. "мнимыми". Однако даже для многих крупных ученых 17 в. алгебраич. и геометрич. сущность мнимых величин представлялась неясной и даже загадочной и мистической. Известно, напр., что И. Ньютон (I. Newton) не включал мнимые величины в понятие числа, а Г. Лейбницу (G. Leibniz) принадлежит фраза: "Мнимые числа - это прекрасное и чудесное убежище божественного духа, почти что амфибия бытия с небытием".
появляющиеся при решении квадратных и кубических уравнений, стали называть, в 16 -17 вв. "мнимыми". Однако даже для многих крупных ученых 17 в. алгебраич. и геометрич. сущность мнимых величин представлялась неясной и даже загадочной и мистической. Известно, напр., что И. Ньютон (I. Newton) не включал мнимые величины в понятие числа, а Г. Лейбницу (G. Leibniz) принадлежит фраза: "Мнимые числа - это прекрасное и чудесное убежище божественного духа, почти что амфибия бытия с небытием". предложил Л. Эйлер (L. Euler, 1777, опубл. 1794). Он же высказал в 1751 мысль об алгобраич. замкнутости поля С, к такому же выводу пришел Ж. Д'Аламбер (J. D'Alembert, 1747), но первое строгое доказательство этого факта принадлежит К. Гауссу (С. Gauss, 1799). Он же ввел в употребление термин "К. ч." в 1831. Полное геометрии, истолкование К. ч. и действий над ними появилось впервые в работе К. Весселя (С. Wessel, 1799). Геометрич. представление К. ч., иногда называемое "диаграммой Аргана", вошло в обиход после опубликования в 1806 и 1814 работы Ж. Р. Аргана (J. R. Argand), повторявшей в основном независимо выводы К. Весселя.
предложил Л. Эйлер (L. Euler, 1777, опубл. 1794). Он же высказал в 1751 мысль об алгобраич. замкнутости поля С, к такому же выводу пришел Ж. Д'Аламбер (J. D'Alembert, 1747), но первое строгое доказательство этого факта принадлежит К. Гауссу (С. Gauss, 1799). Он же ввел в употребление термин "К. ч." в 1831. Полное геометрии, истолкование К. ч. и действий над ними появилось впервые в работе К. Весселя (С. Wessel, 1799). Геометрич. представление К. ч., иногда называемое "диаграммой Аргана", вошло в обиход после опубликования в 1806 и 1814 работы Ж. Р. Аргана (J. R. Argand), повторявшей в основном независимо выводы К. Весселя.