|
"
0
C
F
G
H
K
L
N
P
S
T
W
Z
А
Б
В
Г
Д
Е
Ж
З
И
Й
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Ш
Э
Ю
Я
КОЛМОГОРОВА КРИТЕРИЙЗначение КОЛМОГОРОВА КРИТЕРИЙ в математической энциклопедии: - статистический критерий, применяемый для проверки простой непараметрической гипотезы Н 0, согласно к-рой независимые одинаково распределенные случайные величины Х 1,..., Х п имеют заданную непрерывную функцию распределения F(x), причем альтернативная гипотеза Н 1 предполагается двусторонней:
где
и основано на теореме, доказанной А. Н. Колмогоровым в 1933: в случае справедливости гипотезы Н 0 распределение статистики Dn не зависит от функции F(x), причем если
где
В 1948 Н. В. Смирнов [4] табулировал функцию распределения Колмогорова К(l). Согласно К. к. с уровнем значимости a, 0<a<0,5, гипотезу Н 0 следует отвергнуть, если Для определения ln(a) рекомендуется пользоваться аппроксимацией допредельного закона статистики Колмогорова Dn ее предельным распределением; см. [3], где показано, что если
Применение аппроксимации (*) дает следующее приближение критического значения
где z - корень уравнения На практике для вычисления значения статистики Dn пользуются тем обстоятельством, что
где
Изобразим на плоскости хОу графики функций Fn(x),
Если график функции F(x)не выходит из заштрихованной области, то по К. к. с уровнем значимости а гипотезу H0 следует принять, в противном случае гипотеза H0 отвергается. К. к. дал мощный толчок развитию математич. статистики, в результате чего были получены совершенно новые методы статистич. исследований, к-рые легли в основу непараметрич. статистики. Лит.:[1] Колмогоров А. Н., "Giorn. Istit. Ital. Attuari" 1933, v. 4, p. 83-91; [2] Смирнов Н. В., "Бюлл. МГУ", секц. А, 1939, т. 2, в. 2, с. 3-14; [3] Большев Л. Н., "Теория вероятн. и ее примен.", 1963, т. 8, с. 129-55; [4] Большей Л. Н., Смирнов Н. В., Таблицы математической статистики, 2 изд., М., 1968. М. С. Никулин. |
|
|
|


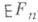 - математическое ожидание функции эмпирического распределения Fn(x). Критическое множество К. к. выражается неравенством
- математическое ожидание функции эмпирического распределения Fn(x). Критическое множество К. к. выражается неравенством
 то
то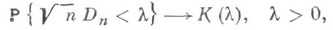

 где ln(a) - критическое значение К. к., соответствующее заданному уровню значимости а и являющееся корнем уравнения
где ln(a) - критическое значение К. к., соответствующее заданному уровню значимости а и являющееся корнем уравнения 
 и
и  то
то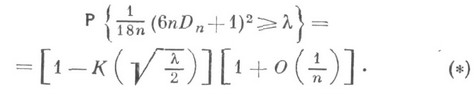



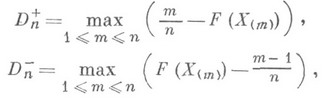
 - вариационный ряд, построенный по выборке X1, ... ,Х п. К. к. имеет следующее геометрич. истолкование (см. рис.).
- вариационный ряд, построенный по выборке X1, ... ,Х п. К. к. имеет следующее геометрич. истолкование (см. рис.). 
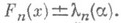 Заштрихованная область является доверительной зоной уровня 1-a. для функции распределения F(x), так как если гипотеза Н 0 верна, то согласно теореме Колмогорова
Заштрихованная область является доверительной зоной уровня 1-a. для функции распределения F(x), так как если гипотеза Н 0 верна, то согласно теореме Колмогорова