|
"
0
C
F
G
H
K
L
N
P
S
T
W
Z
А
Б
В
Г
Д
Е
Ж
З
И
Й
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Ш
Э
Ю
Я
КОД С ИСПРАВЛЕНИЕМ ОШИБОКЗначение КОД С ИСПРАВЛЕНИЕМ ОШИБОК в математической энциклопедии: код, корректирующий ошибки,- множество сообщений, предназначенных для передачи по каналу связи с шумами, обладающее тем свойством, что окрестность ошибок каждого сообщения (т. е. совокупность искаженных вариантов этого сообщения) не пересекается с окрестностями ошибок других сообщений. Это свойство К. с и. о. позволяет правильно корректировать ошибки (т. е. правильно восстанавливать переданное сообщение) в тех (полученных на выходе канала) искаженных сообщениях, к-рые принадлежат своей окрестности ошибок. Элементы К. с и. о. используются при кодировании последовательностей информационных символов, вырабатываемых источником сообщений. Кодирование заключается в представлении информационной последовательности в специальной форме и введении в нее дополнительной информации ( избыточности). Избыточность обычно вводят путем добавления в сообщение тем или иным способом дополнительных символов. Напр., последовательность символов разбивается на блоки фиксированной длины к, а затем независимо один от другого блоки заменяются другими блоками большей длины п, к-рые являются элементами так наз. блокового К. с и. о. Известны [1] и другие способы введения избыточности и связанные с ними К. с и. о. Элементы блокового К. с и. о. выбираются из нек-рого множества га-мерных векторов Ln, снабженного метрикой l(,), а их окрестности ошибок задаются в виде шара с центром в элементе кода. Радиус этого шара определяет корректирующую способность блокового кода. Метрика l(,) зависит от характера ошибок, для исправления к-рых предназначен код. Дальнейшее изложение касается только блоковых К. с и. о. как наиболее распространенных. Для того чтобы иметь возможность передать максимальное количество сообщений по каналу связи, необходимо использовать коды с, максимальным числом элементов при заданной корректирующей способности. Построение таких кодов является одной из основных задач теории К. с и. о. Эта задача достаточно далеко продвинута только для нек-рых рассматриваемых ниже конечных множеств Ln. В то гке время как для приложений, так и для теории интересны коды на нек-рых бесконечных множествах, напр, на сфере в евклидовом пространстве Rn. При практическом использовании К. с и. о. возникают задачи отображения информации, предназначенной для передачи в множество элементов К. с и. о. и нахождения по принятому элементу х' переданного элемента кода х. Первая задача наз. задачей кодирования, вторая - задачей декодирования. Сложность кодирования и декодирования в значительной мере определяется свойствами используемого К. с и. <о. Это обстоятельство приводит к изучению относительно узких классов кодов, как, например, рассматриваемых ниже двоичных линейных кодов. Наиболее широко исследовались блоковые r-и чные коды в метрике Хемминга, ввиду того что они находят многочисленные применения, а методы их построения связаны с известными ранее математическими структурами. Элементами этих кодов являются нек-рые элементы множества В nr, состоящего из всех векторов длины п, координаты к-рых принадлежат множеству из rэлементов. Расстоянием Хемминга d(x, у )между векторами х, у из В nr наз. число их несовпадающих координат. Окрестность ошибок Ut(x)кратности t(t- целое) вектора хсостоит из всех векторов из В nr, отличающихся от хне более чем в r координатах, т. е. Uf(x)- шар в метрике d(,) радиуса tс центром в точке х. В частности, U1 (х). состоит из (r-1)n+1 векторов. Для произвольного множества Для оценки качества конкретных кодов изучают поведение функции m(n, d), равной максимальному числу векторов двоичного кода длины пс кодовым расстоянием d. Относительно хорошо функция т( п, d )изучена при больших d, Код, на к-ром достигается последнее равенство, носит название двоичного кода Хемминга. Двоичный код Хемминга, корректирующий ошибки кратности t=l, обладает следующим свойством: шары радиуса t=l с центрами в точках кода не пересекаются и в то же время заполняют все множество Bn2. Подобные коды наз. совершенными. Известно, что, кроме кодов Хемминга, существует еще лишь конечное число нетривиальных двоичных совершенных кодов. В случае
где
и гарантирует существование кодов с указанными параметрами. Коды с параметрами, лежащими на границе (*), к настоящему времени (1978) могут быть построены только методом перебора. Существенно новые верхние оценки получены в [6], [7]. Весьма правдоподобна гипотеза, по к-рой R(d) = 1-H(d). Далее рассматриваются конструктивные методы (т. е. методы, требующие для своей реализации относительно небольшого числа операций) построения К. с и. о. К важнейшим конструктивным кодам относятся: коды Рида - Соломона (PC-коды), коды Боуза - Чоудхури - Хоквингема (БЧХ-коды) и коды Рида - Маллера (РМ-коды). Перечисленные коды являются линейными. Отправной конструкцией для построения первых двух служит матрица А r с элементами из GF(q):
где а -первообразный корень GF(q). Матрица А r является проверочной матрицей PC-кода С r над GF(q), к-рый имеет следующие параметры: n=q-1, k = q-r, d=r. Кодовое расстояние кода С r является максимальным среди всех линейных кодов длины q-1 и размерности q-r. Двоичный БЧХ-код Н r состоит из всех векторов PC-кода С г над GF(2l), координаты к-рых принадлежат полю GF(2), т. е. Hr=Cr З B2n. БЧХ-код Н r при r=2t+l имеет следующие параметры: п=2l- 1, Двоичный РМ-код определяется как множество двоичных векторов вида (f(a1), f(a2), ..., f(an)), где n=2l, a1, ..., a п- всевозможные двоичные векторы длины lи f(x)пробегает множество всех функций алгебры логики, представимых в виде многочлена над GF(2)степени не выше г от lдвоичных переменных. РМ-код имеет следующие параметры: n=2l, Скорость передачи R(К)двоичного кода Кдлины пс числом векторов топределяется как
Если К- линейный код, то R(K) = k/n. Скорость передачи перечисленных выше конструктивных кодов при При практическом использовании К. с и. о. кратности tдля коррекции ошибок канала связи необходимо устройство (декодер), к-рое по искаженному вектору Достаточно широко исследовались коды на множествах В пq в метриках, отличных от метрики Хемминга. Направление и результаты этих исследований во многом сходны с соответствующими результатами для метрики Хемминга. В частности, рассматривались коды в метриках, связанных с синхронизационными ошибками, с ошибками в арифметич. устройствах ЭВМ (арифметические коды), с пачками ошибок, с несимметричными ошибками, с ошибками в непрерывном канале связи. Напр., в последнем случае множеством Ln является сфера единичного радиуса Sn в евклидовом пространстве Rn с центром в начале координат, а окрестностью ошибок Um(x), Развитие теории К. си. о. стимулировалось работами К. Шеннона (С. Shannon) по теории информации, в к-рых была показана принципиальная возможность передачи по каналу связи с шумами информации со скоростью меньшей пропускной способности канала и произвольной малой ошибкой. Первоначально теория К. с и. о. удовлетворяла потребности техники связи в математических конструкциях, обеспечивающих надежную передачу информации при ограничениях на число и вид ошибок в сообщении. Затем результаты и методы теории К. с и. о. нашли применение в других областях. В частности, в математике этими методами удалось получить наилучшие (к 1978) оценки плотности укладки шаров в евклидовом пространстве, получить значительное продвижение при оценке сложности тупиковых дизъюнктивных форм для почти всех функций алгебры логики, построить нек-рые новые объекты в комбинаторике, построить самокорректирующиеся схемы из функциональных элементов и т. д. Лит.:[1]Питерсон У., Уэлдон Э., Коды, исправляющие ошибки, пер. с англ., 2 изд., М., 1976; [2] Берлекэмп Э., Алгебраическая теория кодирования, пер. с англ., М., 1971; [3] Дискретная математика к математические вопросы кибернетики, т. 1, М., 1974; [4] Блох Э. Л., Зяблов В. В., Обобщенные каскадные коды, М., 1976; [5] Колесник В. Д., МирончиковЕ. Т., Декодирование циклических кодов, М., 1968; [6] Сидельников В. М., "Пробл. передачи информ.", 1974, т. 10, в. 2, с. 43-51; [7] Левейштейн В. И., там же, с. 26-42; [8] Зяблов В. В., Пинскер М. С, "Пробл. передачи информ.", 1975, т. И, в. 1, с. 23-36. В. М. Сиделъников. |
|
|
|

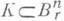 функция
функция 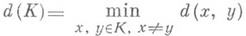 наз. кодовым расстоянием r-ичного кода К. Код Кявляется К. си. о. кратности t, если
наз. кодовым расстоянием r-ичного кода К. Код Кявляется К. си. о. кратности t, если  При выполнении последнего неравенства каждая окрестность ошибок Ut(x),
При выполнении последнего неравенства каждая окрестность ошибок Ut(x),  не пересекается ни с какой другой окрестностью ошибок кратности tвектора уиз К. Значительный прогресс в изучении r-ичных кодов получен для случая, когда г является степенью простого числа. В этом случае в качестве множества координат берут конечное поле GF(q)из qэлементов и используют алгебраические свойства этого понятия. Ниже предполагается, что координатами элементов множества
не пересекается ни с какой другой окрестностью ошибок кратности tвектора уиз К. Значительный прогресс в изучении r-ичных кодов получен для случая, когда г является степенью простого числа. В этом случае в качестве множества координат берут конечное поле GF(q)из qэлементов и используют алгебраические свойства этого понятия. Ниже предполагается, что координатами элементов множества 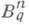 являются элементы поля GF(q). Множество
являются элементы поля GF(q). Множество  является линейным пространством над полем GF(q). Если векторы кода Кобразуют линейное подпространство пространства
является линейным пространством над полем GF(q). Если векторы кода Кобразуют линейное подпространство пространства  то код наз. линейным. Линейный код К может быть задан как своим базисом, так и базисом линейного пространства, двойственного к К. Последний способ более распространен. Матрица А, строками к-рой служат базисные векторы пространства, двойственного к К, наз. проверочной матрицей К. Для векторов
то код наз. линейным. Линейный код К может быть задан как своим базисом, так и базисом линейного пространства, двойственного к К. Последний способ более распространен. Матрица А, строками к-рой служат базисные векторы пространства, двойственного к К, наз. проверочной матрицей К. Для векторов  справедливо соотношение: хА T=0, где А T- транспонированная матрица А. Далее п - длина кода, к- размерность линейного кода и d- кодовое расстояние. Код над
справедливо соотношение: хА T=0, где А T- транспонированная матрица А. Далее п - длина кода, к- размерность линейного кода и d- кодовое расстояние. Код над 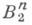 наз. двоичным кодом.
наз. двоичным кодом.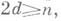 и малых d,d=const,
и малых d,d=const,  В первом случае величина т( п, d )не превосходит 2n при 2d=n и 2dl(2d-n) при 2d-n>0, а во втором - равна по порядку п -t2 п при d=2t+i. Если d=3, n=2l-1, то т(n,3) = 2n/(n+1).
В первом случае величина т( п, d )не превосходит 2n при 2d=n и 2dl(2d-n) при 2d-n>0, а во втором - равна по порядку п -t2 п при d=2t+i. Если d=3, n=2l-1, то т(n,3) = 2n/(n+1).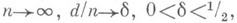 изучают функцию
изучают функцию  (логарифмич. асимптотику m(n, d)), называемую скоростью передачи максимальным кодом с относительным кодовым расстоянием б. Для скорости i?(6) известны существенно различающиеся верхние и нижние оценки. Нижняя оценка (оценка Варшамова - Гилберта) имеет вид
(логарифмич. асимптотику m(n, d)), называемую скоростью передачи максимальным кодом с относительным кодовым расстоянием б. Для скорости i?(6) известны существенно различающиеся верхние и нижние оценки. Нижняя оценка (оценка Варшамова - Гилберта) имеет вид

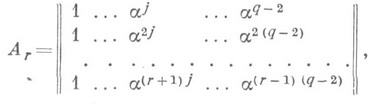
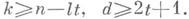 Упомянутый выше код Хемминга совпадает с БЧХ-кодом Н 3. Если t<2[(l+1)/2]([x] - целая часть х), то размерность кода H2t+1 равна п-lt. БЧХ-код является циклическим, т. е. обладает тем свойством, что вместе с вектором хсодержит все его циклнч. сдвиги. Число векторов БЧХ-кодов в случае
Упомянутый выше код Хемминга совпадает с БЧХ-кодом Н 3. Если t<2[(l+1)/2]([x] - целая часть х), то размерность кода H2t+1 равна п-lt. БЧХ-код является циклическим, т. е. обладает тем свойством, что вместе с вектором хсодержит все его циклнч. сдвиги. Число векторов БЧХ-кодов в случае 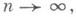 r=const совпадает по порядку с мощностью наилучшего кода т( п, r).
r=const совпадает по порядку с мощностью наилучшего кода т( п, r).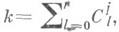 d=2l-r
d=2l-r
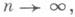
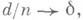 6 >0, стремится к 0. Известны конструктивные коды со скоростью передачи большей нуля при
6 >0, стремится к 0. Известны конструктивные коды со скоростью передачи большей нуля при  но меньшей скорости передачи кодов, существование к-рых устанавливает граница (*).
но меньшей скорости передачи кодов, существование к-рых устанавливает граница (*). указывает переданный кодовый вектор х. При этом предпочтительно использовать такие К. с и. о., для к-рых декодер имеет небольшую сложность. Под сложностью декодера двоичного кода Кс кодовым расстоянием 2t+1 понимается, напр., минимальное число функциональных элементов, к-рое необходимо для реализации булева оператора
указывает переданный кодовый вектор х. При этом предпочтительно использовать такие К. с и. о., для к-рых декодер имеет небольшую сложность. Под сложностью декодера двоичного кода Кс кодовым расстоянием 2t+1 понимается, напр., минимальное число функциональных элементов, к-рое необходимо для реализации булева оператора  Малую сложность декодера имеют рассмотренные конструктивные коды. Кроме того, известны другие К. с и. о. со скоростью передачи, не стремящейся к 0 при
Малую сложность декодера имеют рассмотренные конструктивные коды. Кроме того, известны другие К. с и. о. со скоростью передачи, не стремящейся к 0 при  d>0, и малой сложностью декодера. К таким кодам относятся, напр., каскадные коды и коды с малой плотностью проверок на четность. Каскадный код в простейшем случае представляет собой итерацию PC-кода над полем GF(2l )и двоичного кода длины п 1 размерности lс кодовым расстоянием d1. С помощью какого-либо линейного отображения устанавливается взаимно однозначное соответствие между элементами поля GF(2l). и векторами двоичного кода. Затем координаты PC-кода заменяются соответствующими векторами двоичного кода. В результате получается двоичный линейный каскадный код с параметрами n=n1(2l-1), k=l(2l-r).
d>0, и малой сложностью декодера. К таким кодам относятся, напр., каскадные коды и коды с малой плотностью проверок на четность. Каскадный код в простейшем случае представляет собой итерацию PC-кода над полем GF(2l )и двоичного кода длины п 1 размерности lс кодовым расстоянием d1. С помощью какого-либо линейного отображения устанавливается взаимно однозначное соответствие между элементами поля GF(2l). и векторами двоичного кода. Затем координаты PC-кода заменяются соответствующими векторами двоичного кода. В результате получается двоичный линейный каскадный код с параметрами n=n1(2l-1), k=l(2l-r).  . Лучшие результаты достигаются, если для замены различных разрядов РС-кода использовать различные двоичные коды. Таким способом могут быть получены коды длины n, исправляющие с помощью декодера со сложностью, равной по порядку п log n, фиксированную долю от пошибок. Ансамбль двоичных кодов с малой плотностью проверок на четность определяется ансамблем проверочных матриц {А}, состоящим из двоичных матриц нек-рого вида, размера
. Лучшие результаты достигаются, если для замены различных разрядов РС-кода использовать различные двоичные коды. Таким способом могут быть получены коды длины n, исправляющие с помощью декодера со сложностью, равной по порядку п log n, фиксированную долю от пошибок. Ансамбль двоичных кодов с малой плотностью проверок на четность определяется ансамблем проверочных матриц {А}, состоящим из двоичных матриц нек-рого вида, размера  к-рые содержат в каждом столбце и каждой строке соответственно lи h единиц, 4<l<h. При фиксированных lи hи
к-рые содержат в каждом столбце и каждой строке соответственно lи h единиц, 4<l<h. При фиксированных lи hи  типичный код длины пансамбля с помощью декодера со сложностью, по порядку равной пlog n, может исправлять фиксированную долю от пошибок. Скорость передачи как каскадных, так и кодов с малой плотностью проверок лежит ниже оценки (*).
типичный код длины пансамбля с помощью декодера со сложностью, по порядку равной пlog n, может исправлять фиксированную долю от пошибок. Скорость передачи как каскадных, так и кодов с малой плотностью проверок лежит ниже оценки (*). - поверхность, высекаемая из Sn-1 круговым конусом с полууглом j и с осью, проходящей через точки 0 и х. Следует также заметить, что коды в евклидовом пространстве Rn в несколько иной трактовке рассматривались, начиная с конца 19 в., в геометрии.
- поверхность, высекаемая из Sn-1 круговым конусом с полууглом j и с осью, проходящей через точки 0 и х. Следует также заметить, что коды в евклидовом пространстве Rn в несколько иной трактовке рассматривались, начиная с конца 19 в., в геометрии.