"
0
C
F
G
H
K
L
N
P
S
T
W
Z
А
Б
В
Г
Д
Е
Ж
З
И
Й
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Ш
Э
Ю
Я
КОД С ИСПРАВЛЕНИЕМ ВЫПАДЕНИЙ И ВСТАВОКЗначение КОД С ИСПРАВЛЕНИЕМ ВЫПАДЕНИЙ И ВСТАВОК в математической энциклопедии:
- код, предназначенный для исправления ошибок двух типов, встречающихся при передаче и перфорации информации. Выпадением буквы в слове b=b1 ...bn длины пв нек-ром алфавите Вназ. преобразование слова b в слово b' = b1.. .bi-1bi+1 ...,b п длины п-1,  Для числа Ns(b) слов, получаемых из слова р выпадениями sбукв, справедливы следующие оценки Для числа Ns(b) слов, получаемых из слова р выпадениями sбукв, справедливы следующие оценки 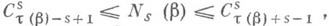 где т(Р) - число серий слова b (серией слова b=b1, ... b п наз. слово где т(Р) - число серий слова b (серией слова b=b1, ... b п наз. слово  такое, что 1) bi+1=...=bj, 2) если такое, что 1) bi+1=...=bj, 2) если  то ' 3) то ' 3) если j<n, то если j<n, то  ). В частности, N1(b)=t(b). Вставкой буквы в слове b=b1 ...b п наз. преобразование слова b в слово b' = b1 ... bibbi.. .bn длины n+1, где ). В частности, N1(b)=t(b). Вставкой буквы в слове b=b1 ...b п наз. преобразование слова b в слово b' = b1 ... bibbi.. .bn длины n+1, где  и и  Число слов, получаемых из произвольного слова b длины пвставками s букв алфавита В, равно Число слов, получаемых из произвольного слова b длины пвставками s букв алфавита В, равно  где r- число букв алфавита В. Множество Кслов в алфавите Вназ. кодом с исправлением s выпадений (вставок, выпадений или вставок), если никакое слово в алфавите Вне может быть получено из двух различных слов из К в результате s или менее выпадений (вставок, выпадений или вставок) букв в каждом из них. Функция, определенная на парах (b1, b2) слов в алфавите Ви равная минимальному числу выпадений и вставок букв, преобразующих b1 в b2, является метрикой. Множество Кслов в алфавите Вявляется кодом с исправлением s выпадений (вставок, выпадений или вставок) тогда и только тогда, когда расстояние между любыми двумя различными словами из Кбольше 2s, так что указанные три определения кодов эквивалентны. Примером кода с исправлением одного выпадения или одной вставки является множество слов {b=b1 ... bn} длины пв алфавите В={0, 1}, для к-рых где r- число букв алфавита В. Множество Кслов в алфавите Вназ. кодом с исправлением s выпадений (вставок, выпадений или вставок), если никакое слово в алфавите Вне может быть получено из двух различных слов из К в результате s или менее выпадений (вставок, выпадений или вставок) букв в каждом из них. Функция, определенная на парах (b1, b2) слов в алфавите Ви равная минимальному числу выпадений и вставок букв, преобразующих b1 в b2, является метрикой. Множество Кслов в алфавите Вявляется кодом с исправлением s выпадений (вставок, выпадений или вставок) тогда и только тогда, когда расстояние между любыми двумя различными словами из Кбольше 2s, так что указанные три определения кодов эквивалентны. Примером кода с исправлением одного выпадения или одной вставки является множество слов {b=b1 ... bn} длины пв алфавите В={0, 1}, для к-рых  . Число слов в этом коде равно . Число слов в этом коде равно  где суммирование производится по всем нечетным делителям dчисла n+1 и j(d) - функция Эйлера, и является асимптотически максимальным при где суммирование производится по всем нечетным делителям dчисла n+1 и j(d) - функция Эйлера, и является асимптотически максимальным при  В. И. Левенштейн.
|

 Для числа Ns(b) слов, получаемых из слова р выпадениями sбукв, справедливы следующие оценки
Для числа Ns(b) слов, получаемых из слова р выпадениями sбукв, справедливы следующие оценки 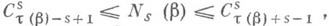 где т(Р) - число серий слова b (серией слова b=b1, ... b п наз. слово
где т(Р) - число серий слова b (серией слова b=b1, ... b п наз. слово  такое, что 1) bi+1=...=bj, 2) если
такое, что 1) bi+1=...=bj, 2) если  то ' 3)
то ' 3) если j<n, то
если j<n, то  ). В частности, N1(b)=t(b). Вставкой буквы в слове b=b1 ...b п наз. преобразование слова b в слово b' = b1 ... bibbi.. .bn длины n+1, где
). В частности, N1(b)=t(b). Вставкой буквы в слове b=b1 ...b п наз. преобразование слова b в слово b' = b1 ... bibbi.. .bn длины n+1, где  и
и  Число слов, получаемых из произвольного слова b длины пвставками s букв алфавита В, равно
Число слов, получаемых из произвольного слова b длины пвставками s букв алфавита В, равно  где r- число букв алфавита В. Множество Кслов в алфавите Вназ. кодом с исправлением s выпадений (вставок, выпадений или вставок), если никакое слово в алфавите Вне может быть получено из двух различных слов из К в результате s или менее выпадений (вставок, выпадений или вставок) букв в каждом из них. Функция, определенная на парах (b1, b2) слов в алфавите Ви равная минимальному числу выпадений и вставок букв, преобразующих b1 в b2, является метрикой. Множество Кслов в алфавите Вявляется кодом с исправлением s выпадений (вставок, выпадений или вставок) тогда и только тогда, когда расстояние между любыми двумя различными словами из Кбольше 2s, так что указанные три определения кодов эквивалентны. Примером кода с исправлением одного выпадения или одной вставки является множество слов {b=b1 ... bn} длины пв алфавите В={0, 1}, для к-рых
где r- число букв алфавита В. Множество Кслов в алфавите Вназ. кодом с исправлением s выпадений (вставок, выпадений или вставок), если никакое слово в алфавите Вне может быть получено из двух различных слов из К в результате s или менее выпадений (вставок, выпадений или вставок) букв в каждом из них. Функция, определенная на парах (b1, b2) слов в алфавите Ви равная минимальному числу выпадений и вставок букв, преобразующих b1 в b2, является метрикой. Множество Кслов в алфавите Вявляется кодом с исправлением s выпадений (вставок, выпадений или вставок) тогда и только тогда, когда расстояние между любыми двумя различными словами из Кбольше 2s, так что указанные три определения кодов эквивалентны. Примером кода с исправлением одного выпадения или одной вставки является множество слов {b=b1 ... bn} длины пв алфавите В={0, 1}, для к-рых  . Число слов в этом коде равно
. Число слов в этом коде равно  где суммирование производится по всем нечетным делителям dчисла n+1 и j(d) - функция Эйлера, и является асимптотически максимальным при
где суммирование производится по всем нечетным делителям dчисла n+1 и j(d) - функция Эйлера, и является асимптотически максимальным при 