"
0
C
F
G
H
K
L
N
P
S
T
W
Z
А
Б
В
Г
Д
Е
Ж
З
И
Й
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Ш
Э
Ю
Я
КОВАРИАНТНЫЙ ТЕНЗОРЗначение КОВАРИАНТНЫЙ ТЕНЗОР в математической энциклопедии:
валентности 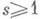 -тензор типа (0, s), элемент тензорного произведения -тензор типа (0, s), элемент тензорного произведения  sэкземпляров пространства Е*, сопряженного (дуального) к векторному пространству Енад полем К. Относительно операции сложения К. т. одной и той же валентности и умножения их на скаляр TS(E)является в свою очередь векторным пространством над К. Пусть Е- конечномерно и пусть e1, ..., е п- базис в Е, а е 1,.. ., е n- сопряженный с ним базис в Е*. Тогда dim Ts(E)=ns и базис в TS(E)состоит из всевозможных разложимых тензоров вида sэкземпляров пространства Е*, сопряженного (дуального) к векторному пространству Енад полем К. Относительно операции сложения К. т. одной и той же валентности и умножения их на скаляр TS(E)является в свою очередь векторным пространством над К. Пусть Е- конечномерно и пусть e1, ..., е п- базис в Е, а е 1,.. ., е n- сопряженный с ним базис в Е*. Тогда dim Ts(E)=ns и базис в TS(E)состоит из всевозможных разложимых тензоров вида   Любой К. г. Любой К. г. 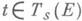 может быть представлен в виде может быть представлен в виде  Числа ti1...is наз. координатами или компонентами К. т. относительно базиса e1 ..., en в Е. При изменении базиса в Епо формулам е i' = а ii' е i и соответственно базиса в Ts(E)координаты К. т. t изменяются по так наз. ковариантному закону Числа ti1...is наз. координатами или компонентами К. т. относительно базиса e1 ..., en в Е. При изменении базиса в Епо формулам е i' = а ii' е i и соответственно базиса в Ts(E)координаты К. т. t изменяются по так наз. ковариантному закону 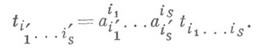
При валентности  К. т. наз. ковариантным век тором;. при К. т. наз. ковариантным век тором;. при  К. т. можно инвариантным образом связать с s-линейным отображением прямого произведения К. т. можно инвариантным образом связать с s-линейным отображением прямого произведения  (s раз) в К, приняв координаты К. т. tотносительно базиса e1 ..., en за значения r-линейного отображения tна базисных в Es векторах (ei1 ..., eis ), и обратно; поэтому иногда К. т. определяют как полилинейный функционал на Es. (s раз) в К, приняв координаты К. т. tотносительно базиса e1 ..., en за значения r-линейного отображения tна базисных в Es векторах (ei1 ..., eis ), и обратно; поэтому иногда К. т. определяют как полилинейный функционал на Es. Лит. см. при статье Ковариантный вектор. И. X. Сабитов.
|

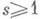 -тензор типа (0, s), элемент тензорного произведения
-тензор типа (0, s), элемент тензорного произведения  sэкземпляров пространства Е*, сопряженного (дуального) к векторному пространству Енад полем К. Относительно операции сложения К. т. одной и той же валентности и умножения их на скаляр TS(E)является в свою очередь векторным пространством над К. Пусть Е- конечномерно и пусть e1, ..., е п- базис в Е, а е 1,.. ., е n- сопряженный с ним базис в Е*. Тогда dim Ts(E)=ns и базис в TS(E)состоит из всевозможных разложимых тензоров вида
sэкземпляров пространства Е*, сопряженного (дуального) к векторному пространству Енад полем К. Относительно операции сложения К. т. одной и той же валентности и умножения их на скаляр TS(E)является в свою очередь векторным пространством над К. Пусть Е- конечномерно и пусть e1, ..., е п- базис в Е, а е 1,.. ., е n- сопряженный с ним базис в Е*. Тогда dim Ts(E)=ns и базис в TS(E)состоит из всевозможных разложимых тензоров вида 
 Любой К. г.
Любой К. г. 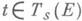 может быть представлен в виде
может быть представлен в виде  Числа ti1...is наз. координатами или компонентами К. т. относительно базиса e1 ..., en в Е. При изменении базиса в Епо формулам е i' = а ii' е i и соответственно базиса в Ts(E)координаты К. т. t изменяются по так наз. ковариантному закону
Числа ti1...is наз. координатами или компонентами К. т. относительно базиса e1 ..., en в Е. При изменении базиса в Епо формулам е i' = а ii' е i и соответственно базиса в Ts(E)координаты К. т. t изменяются по так наз. ковариантному закону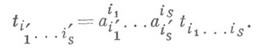
 К. т. наз. ковариантным век тором;. при
К. т. наз. ковариантным век тором;. при  К. т. можно инвариантным образом связать с s-линейным отображением прямого произведения
К. т. можно инвариантным образом связать с s-линейным отображением прямого произведения  (s раз) в К, приняв координаты К. т. tотносительно базиса e1 ..., en за значения r-линейного отображения tна базисных в Es векторах (ei1 ..., eis ), и обратно; поэтому иногда К. т. определяют как полилинейный функционал на Es.
(s раз) в К, приняв координаты К. т. tотносительно базиса e1 ..., en за значения r-линейного отображения tна базисных в Es векторах (ei1 ..., eis ), и обратно; поэтому иногда К. т. определяют как полилинейный функционал на Es.