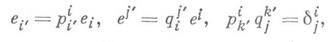|
"
0
C
F
G
H
K
L
N
P
S
T
W
Z
А
Б
В
Г
Д
Е
Ж
З
И
Й
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Ш
Э
Ю
Я
КОВАРИАНТНЫЙ ВЕКТОРЗначение КОВАРИАНТНЫЙ ВЕКТОР в математической энциклопедии: - элемент векторного пространства Е*, сопряженного к re-мерному векторному пространству Е, то есть линейный функционал (линейная форма) на Е. В упорядоченной паре ( Е, Е* )элемент пространства Еназ. контравариантным вектором. В общей схеме построения тензоров К. в. отождествляется с ковариантным тензором валентности 1. Координатная запись К. в. особенно проста, если в Еи Е* выбраны так наз. взаимные, или дуальные, базисы е 1, ..., е п в Еи е 1,..., е n в E*, т. е. такие базисы, что
координаты xi контравариантного вектора х=xi е i изменяются по контравариантному закону xi' = qi'xi, а координаты fi К. в. со изменяются по ковариантному (соизменяющемуся с базисом) закону fi'=pii'ti. Лит.:[1] Широков П. А., Тензорное исчисление, 2 изд., Казань, 1961; [2] Беклемишев Д. В., Курс аналитической геометрии и линейной алгебры, М., 1971 ;[3] Схоутен Я. А., Тензорный анализ для физиков, пер. с англ., М., 1965. И. X. Сабитов. |
|
|
|
(где 
- Кронекера символ);тогда произвольный К. в.
представляется в виде w=fiei (суммирование по i от 1 до n), где fi- значение линейной формы w их вектора е i. При переходе от взаимных базисов ( е i) и ( е j) к взаимным базисам ( е i' )и (ei'). по формулам