|
"
0
C
F
G
H
K
L
N
P
S
T
W
Z
А
Б
В
Г
Д
Е
Ж
З
И
Й
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Ш
Э
Ю
Я
КЛИФФОРДОВА ПОЛУГРУППАЗначение КЛИФФОРДОВА ПОЛУГРУППА в математической энциклопедии: вполне регулярная полугрупп а,- полугруппа, каждый элемент к-рой является групповым, т. е. принадлежит нек-рой подгруппе. Элемент полугруппы будет групповым тогда и только тогда, когда он вполне регулярен (см. Регулярный элемент). Свойство полугруппы Sбыть К. п. эквивалентно каждому из следующих: 1) для любого К. п. наряду с инверсными полугруппами представляют собой один из важнейших типов регулярных полугрупп. Их изучение началось с основополагающей работы А. Клиффорда [1]. Произвольная К. п. обладает (единственным) разбиением на группы, классы к-рого суть в точности Для К. п. Sследующие условия эквивалентны: 1) Sинверсна; 2) каждый идемпотент из Sлежит в центре, т. е. перестановочен с любым элементом из S;3) каждый односторонний идеал полугруппы Sявляется двусторонним; 4) отношения Грина Указанное выше разложение произвольной К. п. в полуструктуру вполне простых полугрупп определяет ее "грубое строение". Закон перемножения элементов в компонентах этого разложения описывает теорема Риса (см. Вполне простая полугруппа). Дальнейшее изучение К. п. в значительной степени направлено на выяснение "тонкого строения", т. е. закона перемножения элементов из различных компонент. В случае, когда эти компоненты - группы, т. е. для инверсных К. п., известно следующее конструктивное описание в терминах так наз. суммы прямого спектра групп. Пусть Тогда Sпревращается в инверсную К. л. Обратно, каждая инверсная К. п. может быть получена указанным способом. В общем случае проблема "тонкого строения" К. п. чрезвычайно усложняется, и удовлетворительного ее решепия пока (1978) нет. Некоторые весьма сложные конструкции, описывающие К. п. в терминах вполне простых полугрупп, их сдвиговых оболочек, полуструктур, отображений со специальными свойствами, приведены в [5]. Больший прогресс достигнут в случае ортодоксальных К. п. (см. Регулярная полугруппа);такие полугруппы наз. ортогруппами. Для них имеется несколько обозримых, хотя и довольно громоздких конструкций (см. [2]). Все упомянутые конструкции так или иначе обобщают приведенное выше описание инверсных К. п., полученное в [1]. Лит.:[1] Clifford A., "Ann. Math.", 1941, V. 42, № 4, p. 1037-49; [2] его же, "J. Pure and Appl. Algebra", 1976, v. 8, № 1, p. 23-50; [3] Клиффорд А., Престон Г., Алгебраическая теория полугрупп, пер. с англ., т. 1-2, М., 1972; [4] Ляпин Е. С, Полугруппы, М., 1960; [5] Реtriсh M., "Trans. Amer. Math. Soc", 1974, v. 189, p. 211-36. Л. Н. Шеврин. |
|
|
|

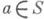 имеет место
имеет место  2) каждый односторонний идеал Iиз Sизолирован, т. е. из того, что
2) каждый односторонний идеал Iиз Sизолирован, т. е. из того, что  следует
следует  при любом натуральном п.
при любом натуральном п. -классы (см. Грина отношения эквивалентности). Указанное разбиение не всегда будет связкой (см. Связка полугрупп);условия, когда это так, известны (см. [3]). Отношения Грина
-классы (см. Грина отношения эквивалентности). Указанное разбиение не всегда будет связкой (см. Связка полугрупп);условия, когда это так, известны (см. [3]). Отношения Грина  и
и  на К. п. совпадают. Всякая вполне простая полугруппа будет К. п., причем для К. п. свойство быть вполне простой эквивалентно идеальной простоте (см. Простая полугруппа). Произвольная К. п. Sразлагается в полуструктуру вполне простых полугрупп, это разложение единственно, его компоненты суть в точности
на К. п. совпадают. Всякая вполне простая полугруппа будет К. п., причем для К. п. свойство быть вполне простой эквивалентно идеальной простоте (см. Простая полугруппа). Произвольная К. п. Sразлагается в полуструктуру вполне простых полугрупп, это разложение единственно, его компоненты суть в точности  -классы, а соответствующая факторполуструктура изоморфна полуструктуре главных идеалов полугруппы S;обратно, всякая полугруппа, разложимая в полуструктуру вполне простых полугрупп, есть К. п.
-классы, а соответствующая факторполуструктура изоморфна полуструктуре главных идеалов полугруппы S;обратно, всякая полугруппа, разложимая в полуструктуру вполне простых полугрупп, есть К. п. и
и  на Sсовпадают; 5) Sесть полуструктура групп; 6) Sразложима в подпрямое произведение групп и групп с присоединенным нулем.
на Sсовпадают; 5) Sесть полуструктура групп; 6) Sразложима в подпрямое произведение групп и групп с присоединенным нулем. - семейство попарно непересекающихся групп, А- полуструктура (см. Идемпотентов полугруппа )и каждой паре элементов
- семейство попарно непересекающихся групп, А- полуструктура (см. Идемпотентов полугруппа )и каждой паре элементов 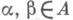 таких, что
таких, что  поставлен в соответствие гомоморфизм
поставлен в соответствие гомоморфизм  причем ja, a для любого а есть тождественный автоморфизм и для любых
причем ja, a для любого а есть тождественный автоморфизм и для любых  имеет место ja, b Хjb, g=ja, g . На объединении
имеет место ja, b Хjb, g=ja, g . На объединении  зада-, ется умножение Х, а именно, аХb=аХja, abbja, ab для любых
зада-, ется умножение Х, а именно, аХb=аХja, abbja, ab для любых  и
и 