|
"
0
C
F
G
H
K
L
N
P
S
T
W
Z
А
Б
В
Г
Д
Е
Ж
З
И
Й
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Ш
Э
Ю
Я
КЛАССИЧЕСКИЕ ОРТОГОНАЛЬНЫЕ МНОГОЧЛЕНЫЗначение КЛАССИЧЕСКИЕ ОРТОГОНАЛЬНЫЕ МНОГОЧЛЕНЫ в математической энциклопедии: - общее название Якоби многочленов, Эрмита 'многочленов, Лагерра многочленов и Чебышева многочленов. Эти системы ортогональных многочленов обладают общими свойствами: 1) Весовая функция j(х)на интервале ортогональности ( а, b )удовлетворяет дифференциальному уравнению Пирсона
причем на концах интервала ортогональности выполняются условия
2) Многочлен у=Р п (х)порядка пудовлетворяет дифференциальному уравнению
3) Имеет место обобщенная Родрига формула
4) Производные К. о. м. суть также К. о. м. и ортогональны на том же интервале ортогональности, вообще говоря, с другим весом. 5) Для производящей функции
имеет место представление
где l=l{х, w)- тот корень квадратного уравнения z-х-wB(z)=0, который при малых |w| ближе расположен к точке х. Этими свойствами обладают только три из указанных систем ортогональных многочленов, а также системы, полученные из этих трех линейными преобразованиями независимого переменного. В обобщенной формуле Родрига нормировочный коэффициент с п обычно выбирается тремя различными способами с целью получения ортонормированных многочленов, либо ортогональных многочленов с единичным старшим коэффициентом, либо так наз. стандартизованных ортогональных многочленов, к-рые вводятся потому, что наиболее удобны в применениях и основные формулы для них имеют наиболее простой вид. К. о. м. являются собственными функциями нек-рых задач на собственные значения для уравнений типа Штурма - Лиувилля, причем в этих задачах каждая система ортогональных многочленов (многочлены Якоби, многочлены Эрмита, многочлены Лагерра) является единственной последовательностью решений соответствующей системы уравнений (см. [4], с. 110). Частные случаи К. о. м. определяются следующим выбором весовой функции и интервала ортогональности: 1) Многочлены Якоби {Р п (х;a, b} ортогональны на сегменте [-1,1] с весом j(х)=(1-x)a(i+x)b, где a>-1, b>-1. В частности, при a=b имеем ультрасферические многочлены, или многочлены Гегенбауэра {Р п (х;a)}. Лежандра многочлены {Р n (х)}соответствуют значениям a=b=0 и ортогональны на сегменте [ - 1,1] с весом j(x)=1. Если 2) Многочлены Эрмита {Н n (х)}ортогональны на интервале 3) Многочлены Лагерра {L п (х;a)}ортогональны на интервале Лит.:[1] Геронимус Я. Л., Теория ортогональных многочленов, М.-Л., 1950; [2] Бейтмен Г., Эрдейи А., Высшие трансцендентные функции. Т. 2, Функции Бесселя, функции параболического цилиндра, ортогональные многочлены, пер. с англ., 2 изд., М., 1974; [3] Джексон Д., Ряды Фурье и ортогональные полиномы, пер. с англ., М., 1948; [4] Никифоров А. Ф., Уваров В. Б., Основы теории специальных функций, М., 1974; [5] Суетин П. К., Классические ортогональные многочлены, М., 1976. См. также лит. при ст. Ортогональные многочлены. П. И. Суетин. |
|
|
|

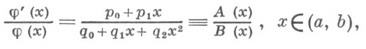


 где с п- некоторый нормировочный коэффициент.
где с п- некоторый нормировочный коэффициент.

 т. е. j(x)=[(1-х)(1+х)]-1/2, то имеем многочлены Чебышева первого рода {Т п (х)}, а при
т. е. j(x)=[(1-х)(1+х)]-1/2, то имеем многочлены Чебышева первого рода {Т п (х)}, а при  - многочлены Чебышева второго рода {Un(x)}.
- многочлены Чебышева второго рода {Un(x)}. с весом j(x) = ехр(- х 2)
с весом j(x) = ехр(- х 2) с весом j(x) = xae-x, где a>-1.
с весом j(x) = xae-x, где a>-1.