|
"
0
C
F
G
H
K
L
N
P
S
T
W
Z
А
Б
В
Г
Д
Е
Ж
З
И
Й
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Ш
Э
Ю
Я
КЕЛДЫША - ЛАВРЕНТЬЕВА ПРИМЕРЗначение КЕЛДЫША - ЛАВРЕНТЬЕВА ПРИМЕР в математической энциклопедии: - пример односвязной области D плоскости комплексного переменного z, ограниченной спрямляемой кривой Жордана, но не принадлежащей классу областей Смирнова S. Пусть функция z=/(w) реализует конформное отображение единичного круга Е- {w;|w|<1} на односвязную область D, ограниченную спрямляемой кривой Жордана. Известно, что f(w)непрерывна в замкнутом круге
где m - нормированная борелевская мера на дЕ, Класс Sсостоит из таких областей D, для М. В. Келдыш и М. А. Лаврентьев [1] построили для любого k,0<h<1, односвязную область Д, ограниченную спрямляемой кривой Жордана Г, расположенную в круге |z|<h,
произвольной дуге кривой Г на окружности дЕ={w; | w|= 1} соответствует дуга той же длины. Эта область D не принадлежит классу S, так как Проблема характеризации областей класса S(областей типа Смирнова) до сих пор (1978) полного решения не получила (см. [2], [3]). Лит.:[1] Келдыш М. В., Лаврентьев М. А., "Ann. Ecole norm, super.", 1937, t. 54, p. 1 - 38; [2] Привалов И. И., Граничные свойства аналитических функций, 2 изд., М.- Л., 1950; [3] Ловатер Дж., в кн.: Итоги науки и техники. Математический анализ, т. 11, М., 1973, с. 99-179. Е. Д. Соломенцев. |
|
|
|
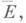а логарифм модуля производной In f'(w)представим в Еинтегралом Пуассона - Стилтьеса
к-рых мера m. в представлении (*) абсолютно непрерывна по мере Лебега на дЕ и интеграл (*) превращается в интеграл Пуассона - Лебега от существующих почти всюду на дЕ граничных значений ln |f'(eiq)|.
и такую, что при конформном отображении области D на круг Е,
=0 почти всюду на дЕ.