|
"
0
C
F
G
H
K
L
N
P
S
T
W
Z
А
Б
В
Г
Д
Е
Ж
З
И
Й
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Ш
Э
Ю
Я
КЁБЕ ТЕОРЕМАЗначение КЁБЕ ТЕОРЕМА в математической энциклопедии: - 1) К. т. покрытия: существует абсолютная постоянная К>0 (постоянная Кёбе) такая, что если
где a- действительное число. К. т. покрытия иногда формулируют так: если функция w=f(z), f(0) = 0, регулярна и однолистна в |z|<l и отображает круг |z| <1 на область, не содержащую точку с, то |f'(0)|<4с. 2) К. т. искажения, а) Существуют такие положительные числа m1(r), М 1(r), зависящие только от r, что для
б) Существует число М(r), зависящее только от r и такое, что для
Эту теорему можно также сформулировать следующим образом: существуют положительные числа т 2(r), М 2(r), зависящие только от r и такие, что для
Л. Бибербах показал, что наилучшие границы в К. т. искажения таковы:
3) К. т. об отображении конечно связных областей на канонические области, а) Всякую n-связную область Вплоскости z можно однолистно отобразить на круговую область (т. е. на область, ограниченную конечным числом полных окружностей без общих точек, причем нек-рые из них могут вырождаться в точки) плоскости z. Среди этих отображений существует только одно нормированное отображение, переводящее заданную точку
смотря по тому, конечно аили нет. б) Всякую n-связную область В плоскости z с граничными континуумами К 1, ..., К п можно однолистно отобразить на плоскость z с празрезами по дугам логарифмич. спиралей соответственно наклонов q1, ...,qn,
смотря по тому, конечно bили нет. Отображение единственно. Теоремы 1) - 3) установлены П. Кёбе (см.[1] - [4]). Лит.:[1] Коеbe P., "Nachr. Kgl. Ges. Wiss. Gott., Math - Phys. Kl.", 1907, Bd 2, S. 191-210; 1909, Bd 4, S. 68 - 76; [2] его же, "Math. Ann.", 1910, Bd 69, S. 1-81; 13] eго же "Acta Math.", 1918, v. 41, p. 305 - 44; [4] eго же, "Math. Z.", 1918, Bd 2, S. 198-236; [5] Голузин Г. М., "Успехи ыатем. наук", 1939, в. 6, с. 26-89; [6] его же, Геометрическая теория функций комплексного переменного, 2 изд., М., 1966; [7] Дженкинс Дж., Однолистные функции и конформные отображения, пер. с англ., М., 1962. Е. Г. Голузина. |
|
|
|

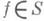 (S- класс функций f(z) = z + . .. , регулярных и однолистных в |z|< 1), то множество значений функции w=f(z)при |z|<l заполняет круг |w|<K, причем К- наибольшее из чисел, для к-рых это справедливо. Л. Бибербах (L. Bieberbach, 1916) доказал, что
(S- класс функций f(z) = z + . .. , регулярных и однолистных в |z|< 1), то множество значений функции w=f(z)при |z|<l заполняет круг |w|<K, причем К- наибольшее из чисел, для к-рых это справедливо. Л. Бибербах (L. Bieberbach, 1916) доказал, что  и что на окружности |w|=1/4 только в том случае имеются точки, не принадлежащие образу круга |z|<1 при отображении w=f(z), если
и что на окружности |w|=1/4 только в том случае имеются точки, не принадлежащие образу круга |z|<1 при отображении w=f(z), если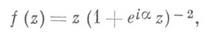
 |z| = r имеют место неравенства:
|z| = r имеют место неравенства: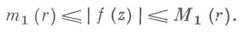
 справедливы неравенства:
справедливы неравенства: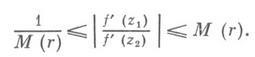




 в
в  и такое, что разложение отображающей функции в окрестности z=a имеет вид
и такое, что разложение отображающей функции в окрестности z=a имеет вид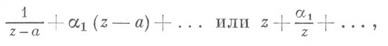
 v=l, . . ., n, к радиальным направлениям и притом так, что континуумы Kv,v=l,..., п, переходят соответственно в дуги наклонов qv, заданные точки
v=l, . . ., n, к радиальным направлениям и притом так, что континуумы Kv,v=l,..., п, переходят соответственно в дуги наклонов qv, заданные точки  переходят в 0 и
переходят в 0 и 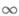 и разложение отображающей функции в окрестности z=b имеет вид
и разложение отображающей функции в окрестности z=b имеет вид