|
"
0
C
F
G
H
K
L
N
P
S
T
W
Z
А
Б
В
Г
Д
Е
Ж
З
И
Й
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Ш
Э
Ю
Я
КВАНТОВАЯ ТЕОРИЯ ПОЛЯЗначение КВАНТОВАЯ ТЕОРИЯ ПОЛЯ в математической энциклопедии: - теория релятивистских квантовых систем. Возникновение К. т. п. связано с задачами о взаимодействии вещества с излучением и с попытками построения релятивистской квантовой механики [П. Дирак (P.A.M. Dirac, 1927), В. Гейзенберг (W. Heisenberg), В. Паули (W. Pauli) и др.]. При релятивистских (т. <е. больших) энергиях не может быть последовательной квантовой механики частицы, так как релятивистская квантовая частица способна порождать новые (такие же или другие) частицы, а сама - исчезать. Вследствие этого нельзя выделить нек-рое число механич. степеней свободы, связанных с этой частицей, а приходится говорить о системе с переменным, вообще говоря, бесконечным числом степеней свободы. К. т. п. объединяет описание полей и частиц, к-рые в классич. физике выступают как две разные сущности. Центральную роль в теории играет понятие квантового поля. Удобно пояснить, как оно вводится, на примере электромагнитного поля, так как это единственное поле, имеющее ясное содержание и в классическом и в квантовом случаях. Классическое электромагнитное поле удовлетворяет уравнениям Максвелла. Эти уравнения можно переписать в виде канонических уравнений Гамильтона, так что потенциал поля играет роль координаты, а его производная по времени - импульса в соответствующем фазовом пространстве. Поле представляется как каноническая система с бесконечным числом степеней свободы, так как потенциал в каждой пространственной точке есть независимая координата. Эту систему можно квантовать так же, как обычную механич. систему. В квантовой картине основные понятия - это состояния, описываемые векторами гильбертова пространства, и наблюдаемые, описываемые самосопряженными операторами, действующими в этом пространстве. Квантование состоит в замене канонических координат и импульсов на операторы таким образом, чтобы скобке Пуассона сопоставлялся коммутатор соответствующих операторов. Квантовое поле становится оператором, действующим на векторы состояния и вызывающим переходы между состояниями с различным числом квантовых частиц - фотонов, т. е. описывающим рождение и уничтожение (излучение и поглощение) квантов, поля. Аналогично квантовое поле может быть поставлен" в соответствие любым другим фундаментальным частицам. Уравнения для оператора свободного поля получаются из основного требования теории относительности - условия инвариантности относительно Пуанкаре группы. Сорт частиц характеризуется массой покоя т, спином, т. е. собственным моментом s, принимающим целые и полуцелые значения, включая нуль, и различными зарядами (электрическим, барионным, лептонным и т. д.). Первые два числа [ т, s]определяют неприводимое представление группы Пуанкаре, по к-рому преобразуется поле, а тем самым и уравнения поля. Свободное классическое скалярное поле и(х)подчиняется уравнению
Это - вариационное уравнение Эйлера для функционала действия
с плотностью лагранжиана
Если рассматривать u(x),
{h- постоянная Планка, далее принимается h=1). Оператор Гамильтона имеет вид:
т. е. Н 0- та же функция квантовых операторов ер и я, что и классич. гамильтониан, с точностью до порядка {не коммутирующих) операторов. Символ :: нормального произведения уточняет этот порядок. Гамильтоновы уравнения движения
эквивалентны уравнению
Квантовое поле в 4-мерном пространстве-времени необходимо является обобщенной, а не обыкновенной операторнозначной функцией, поэтому j(x)следует понимать только как символическую запись. Математич. смысл этим символам придается в формализме пространства Фока, представляющего собой реализацию пространства состояний в К. т. п. Состояние одной частицы в заданный момент времени описывается комплексной функцией Y( р), квадратично интегрируемой по релятивистски инвариантной мере
где w( р)=( р2+т 2)1/2 -релятивистская энергия частицы с массой т. Такие функции образуют гильбертово пространство
где (р, a)=pmam = p0a0- pa - лоренц-инвариантная билинейная форма. Представление, заданное в Различные операторы, в фоковском пространстве выражаются через операторы рождения и уничтожения. Пусть f(p)- одночастичная волновая функция (т. е.
а оператор рождения а*(f) :
Фурье-преобразование суммы операторов рождения и уничтожения
и как операторная обобщенная функция j(х)удовлетворяет на своей области определения уравнению (2) и каноническим коммутационным соотношениям
Таким образом, в фоковском пространстве реализуется каноническое квантование, описанное выше. Теория свободного квантового поля может быть изложена математически строго и последовательно. Для взаимодействующих полей положение иное. Хотя в К. т. п. и получен целый ряд важных результатов по проблемам, допускающим корректную математическую постановку, но до сих пор не решена принципиальная задача обоснования теории взаимодействующих полей: не построено нетривиального примера, удовлетворяющего всем физич. требованиям. Конкретные физич. расчеты опираются на эвристическую схему К. т. п., в основе к-рой в большинстве случаев лежит теория возмущений. Уравнение для взаимодействующего поля содержит нелинейный член - j(Ф(х)): Это уравнение, так же как (1), может быть получено как вариационное уравнение для Лагранжиан взаимодействия
где, однако, в экспоненте стоит уже полный гамильтониан
Выбирая в качестве начальных данных значения свободного поля j(x) и p(x), можно выразить решение нелинейного уравнения (4) через операторы рождения и уничтожения а*( р )и а( р )свободных частиц. В этой схеме приходится вводить в рассмотрение невзаимодействующие частицы и рассматривать взаимодействие как дополнительный фактор, к-рый в последовательном изложении приходится "включать" и "выключать" с помощью специальной адиабатической процедуры (см. [5]). Между тем взаимодействие может весьма заметно менять спектр и другие характеристики рассматриваемых полей. В стандартных методах считается, что полю Ф отвечает именно та частица, к-рая проявляется в линеаризованном уравнении. Только для достаточно слабого взаимодействия типа lФ 4 можно доказать, что это так. Однако и в теории возмущений спектр, вообще говоря, меняется. Собственный вектор Q, отвечающий минимальному собственному значению дискретного спектра Н(точнее, следовало бы говорить об операторе массы) наз. перенормированным вакуумом и интерпретируется как состояние без частиц. Собственные значения, отвечающие остальным точкам дискретного спектра, называются перенормированными одночастичными состояниями (обычно считается, что имеется одно такое состояние). Оно отличается от состояния а*(f)W0 и имеет массу М, отличную от затравочной массы т. Прямое применение теории возмущений дает бессмысленные расходящиеся выражения (так наз. "ультрафиолетовые расходимости"). Если регуляризацию этих расходимостей проводить в соответствии с физическими принципами (главным условием оказалась релятивистская и калибровочная инвариантность всей процедуры), то весь произвол (в электродинамике) сводится к формально бесконечной перенормировке массы и заряда электрона, как было показано в 1948 Ю. Швингером (J. Schwinger), P. Фейнманом (R. Р. Feynman) и Ф. Дайсоном (F. J. Dyson). Окончательную формулировку и строгий математич. анализ К. т. п. в рамках теории возмущений дал II. Н. Боголюбов (1951 - 55). Он указал, что ультрафиолетовые расходимости в теории возмущений появляются вследствие перемножения обобщенных функций в точках, где их носители пересекаются, и сформулировал такой способ их перемножения, при к-ром выполняются физич. требования релятивистской инвариантности, причинности и др. В практич. расчетах теория возмущений применяется не непосредственно к уравнению (4), а к различным другим объектам, к-рые могут быть из него получены, напр, к S-матрице (см. Рассеяния матрица )или к функциям Грина. Вычисление S-матрицы является одной из главных задач в физике элементарных частиц. Ее матричные элементы просто где Т(. ..)- символ хронологического упорядочения
Разлагая Gn в ряд по степеням
можно выразить ее в каждом порядке теории возмущений через интегралы от произведений простейших функций Грина свободного поля
Для вычислений по теории возмущений разработана техника диаграмм Фейнмана. При этом возникают произведения функций Грина D(х)в совпадающих точках. Напр., функция G2(x1, х 2 )для модели
Этот интеграл расходится, однако его можно регуляризовать, т. е. сопоставить ему нек-рое осмысленное выражение. Прежде всего следует придать смысл произведению обобщенных функций D3(x). Это можно сделать следующим образом. Рассматривается сглаженная функция
где e>0, а
Найдутся такие константы ax и b х (расходящиеся при
Функция D3reg(x) и является регуляризацией D3(x). Она определяется с точностью до слагаемых
в каждом порядке разложения в ряд по l. при х стремящимся к бесконечности , получаются конечные выражения. Если в данной модели возможно устранить ультрафиолетовые расходимости с помощью добавления контрчленов той же структуры, что и исходный лагранжиан, то такая модель называется перенормируемой; в противном случае - неперенормируемой. Все модели скалярного поля, взаимодействие в к-рых есть полином степени выше четвертой - неперенормируемы. Это относится только к теории возмущений. Последовательная формулировка описанного способа отделения "бесконечностей", возникающих при перемножении сингулярных обобщенных функций во всех порядках теории возмущений, составляет содержание так наз. теоремы об "R-операции" Н. Н. Боголюбова и О. С. Парасюка (1956) [5], [19]. Тем самым была доказана теорема существования квантовой теории взаимодействующих полей во всех порядках теории возмущений. Последующие исследования показали, что ряд теории возмущений является в лучшем случае асимптотическим, и оценки на его основе применимы только при не слишком больших энергиях участвующих в процессе частиц. Устранение ультрафиолетовых расходимостей удается последовательно провести только в рамках тзории возмущений. Все вышесказанное относилось к реальному четырехмерному пространству-времени. В трехмерном пространстве-времени взаимодействие становится менее сингулярным и можно ограничиться добавлением контрчлена В х: u2, причем В к. имеет второй порядок по X. В двумерном пространстве-времени контрчлены не нужны. Здесь описана только простейшая модель скалярного поля с взаимодействием lФ 4. В К. т. п. имеют дело с более сложными многокомпонентными системами взаимодействующих ферми- и бозе-полей. Напр., киральные поля уже на классич. уровне принимают значения в нек-рых не обязательно линейных однородных пространствах (напр., на сфере); калибровочные поля являются связностями в нек-рых векторных расслоениях - к ним относятся электромагнитное поле, гравитационное поле и поле Янга - Миллса (см. [11], [15]). Метод возмущений не применим в тех случаях, когда константа взаимодействия - основной параметр разложения - заведомо больше единицы, как для сильных ядерных взаимодействий мезонов и нуклонов. Для сильных взаимодействий пользуются другими методами, в к-рых существенную роль играют рассмотрение S-матрицы в целом и изучение общих свойств ее матричных элементов, прямо описывающих интересные для опыта величины - амплитуды процессов рассеяния и рождения. При этом квантовые поля (или токи), к-рые могут быть выражены через S-матрицу, играют важную роль, поскольку на S-матрицу накладывается центральное условие причинности (Н. Н. Боголюбов, 1955) как ограничение на носитель определенных матричных элементов S-матрицы. Вместе с другими физич. требованиями, такими, как релятивистская инвариантность и характер энергетического спектра, условие причинности позволяет установить свойства голоморфности обобщенных функций - амплитуд рассеяния как функций нескольких комплексных переменных. Эти аналитич. свойства оказываются достаточными для вывода специального рода интегральных представлений для амплитуды рассеяния - "дисперсионных соотношений". Строгое доказательство дисперсионных соотношений [4] потребовало развития специальных математич. методов, лежащих на стыке теории обобщенных функций и теории функций многих комплексных переменных и, в частности, доказательства теоремы об острие клина Н. Н. Боголюбова и о С-выпуклой оболочке В. С. Владимирова [8]. Дисперсионные соотношения стали основой большей части конкретных методов расчета в теории сильных взаимодействий [А. А. Логунов, С. Мандельстам (S. Mandelstam) и др.]. Они примыкают к так наз. аксиоматической теории поля, в к-рой выясняются совместность аксиом и их следствия, касающиеся вопросов существования и свойств квантовых полей. Метод теории возмущений предполагает, что для уравнения (4), решением к-рого является квантовое поле Ф(х), выбираются простейшие начальные данные j, p, заданные в фоковском пространстве свободных частиц. Существует много унитарно неэквивалентных реализаций (представлений) коммутационных соотношений (3), и в этом состоит отличие К. т. п. как системы с бесконечным числом степеней свободы от квантовой механики, где имеется теорема Неймана о единственности этих представлений. Для физики интересны любые реализации начальных данных, для к-рых уравнение (4) имеет решения Ф(х), и гамильтониан II ограничен снизу. Гильбертово пространство, в к-ром реализовано такое представление, наз. сектором. Нек-рые модели могут иметь по нескольку фаз (фаза - сектор с единственным вакуумом), напр., lФ 4 -модель имеет при достаточно больших Xдве фазы - происходит фазовый переход. При построении фаз применяется квазисредних метод. Представление о фазовом переходе и связанном с ним явлении спонтанного нарушения симметрии сыграло важную роль в частности в единой теории слабых и электромагнитных взаимодействий. В 1974 было показано, что в нек-рых двумерных моделях имеются так наз. солитонные сектора, в к-рых вакуум отсутствует, но к-рые имеют богатый спектр частиц, аналогичный спектру частиц соответствующей классич. модели (Л. Д. Фаддеев и др.). В К. т. п. имеется много задач, требующих для своего решения методов из различных областей математики, в настоящее время интенсивно исследуемых. Условно их можно разбить на следующие группы. 1) Анализ аксиом и их следствий для квантовых полей и S-матрицы. Помимо средств функционального анализа - теории самосопряженных операторов, обобщенных функций, представлений групп,- здесь используются методы теории функций многих комплексных переменных, С*-алгебры и алгебры Неймана, в последнее время - методы теории вероятностей. Основные величины - функции Грина или функции Уайтмана wn(x1,..., х п)- являются граничными значениями функций, голоморфных в некоторых областях Для ряда моделей в двух- и трехмерном пространстве-времени доказано, что значения функций Уайтмана в этих точках являются моментами вероятностной меры. Заслуживает внимания дальнейший анализ такого евклидова подхода к К. т. п. с точки зрения теории вероятностей. Имеется общий алгебраич. подход к теории поля, при к-ром в основу теории кладутся алгебры наблюдаемых - т. е. С*-алгебры или алгебры Неймана, наделенные нек-рыми естественными с физич. точки зрения структурными свойствами. Здесь одна из основных задач состоит в анализе связи между алгебрами полей и алгебрами наблюдаемых, а также задача об описании динамики в рамках этого подхода. 2) Конструктивная К. т. п. имеет важнейшей задачей доказательство существования моделей К. т. п. в 4-мерном пространстве-времени. В двух- и трехмерном случае существование ряда моделей доказано на основе евклидова (вероятностного) подхода с применением методов, развитых по аналогии со статистической механикой; здесь требуется дальнейший математич. анализ таких вопросов, как спектр гамильтониана, фазовые переходы, свойства S-матрицы и др. 3) В формальной К. т. п., существование к-рой известно в каждом порядке теории возмущений, также имеется ряд проблем, допускающих математич. формулировку. Сюда относятся, напр., анализ рядов теории возмущений (в частности, аналитич. свойства диаграмм Фейнмана), изучение классич. уравнений теории поля и квазиклассических поправок к ним - здесь возникают нелинейные уравнения эллиптического и гиперболического типов, для анализа к-рых применяются, в частности, метод обратной задачи рассеяния, методы дифференциальной и алгебраической геометрии и топологии, и др. Лит.:[1] Ахиезер А. И., Берестецкий В. Б., Квантовая электродинамика, 3 изд., М., 1969; [2] Березин Ф. А., Метод вторичного квантования, М., 1965; [3] Боголюбов Н. Н.,Логунов А. А., Тодоров И. Т., Основы аксиоматического подхода к квантовой теории поля, М., 1969; [4] Боголюбов Н. Н., Медведев Б. В., Поливанов М. К., Вопросы теории дисперсионных соотношений, М., 1958; [5] Боголюбов Н. Н., Ширков Д. В., Введение в теорию квантованных полей, 3 изд., М., 1976; [6] Вайтман А., Проблемы в релятивистской динамике квантованных полей, пер. с англ., М., 1968; [7] Васильев А. Н., Функциональные методы в квантовой теории поля и статистике, Л., 1976; [8] Владимиров В. С, Методы теории Функций многих комплексных переменных, М., 1964; [9] Йост Р., Общая теория квантованных полей, пер. с англ., М., 1967; [10] Конструктивная теория поля, пер. с англ., ИГ., 1977; [11] Попов В. Н., Континуальные интегралы в квантовой теории поля и статистической физике, М., 1976; [12] Рид М., Саймон Б., Методы современной математической физики, пер. с англ., т. 1, М., 1977, т. 2, М., 1978; [13] Саймон Б., Модель Р(j)2 эвклидовой квантовой теории поля, пер. с англ., М., 1976; [14] Сигал И., Математические проблемы релятивистской физики, пер. с англ., М., 1968; [15] Славнов А. А., Фаддеев Л. Д., Введение в теорию калибровочных полей, М., 1978; [16] Стритер Р., Вайтман А., РСТ, спин и статистика и все такое, пер. с англ., М., 1966; [17] Фам Ф., Введение в топологическое исследование особенностей Ландау, пер. с франц., М., 1970; [18] Фридрихе К., Возмущение спектра операторов в гильбертовом пространстве, пер. о англ., М., 1969; [191 Xепп К., Теория перенормировок, пер. с франц., М., 1974; [20] Шварц А. С, Математические основы квантовой теории поля, М., 1975; [21] Швебер С, Введение в релятивистскую квантовую теорию поля, пер. с англ., М., 1963; [22] Квантовая теория калибровочных полей, пер. с англ., М., 1977. И. В. Волович, М. К. Поливанов. |
|
|
|





 как каноническую координату, то сопряженный импульс есть
как каноническую координату, то сопряженный импульс есть  =
= =
= (точка означает производную по времени). Квантование выполняется посредством сопоставления функциям и(x), р(x)операторных функций j(х), p(x), удовлетворяющих коммутационным соотношениям (квантовой скобке Пуассона)
(точка означает производную по времени). Квантование выполняется посредством сопоставления функциям и(x), р(x)операторных функций j(х), p(x), удовлетворяющих коммутационным соотношениям (квантовой скобке Пуассона)




 Система из птождественных частиц описывается квадратично интегрируемой функцией Y п( р 1, ..., р п), симметричной (для бозонов - частиц с целым спином) или антисимметричной (для фермионов - частиц с полуцелым спином) относительно перестановки любых двух координат. Эти функции (для бозонов) принадлежат гильбертову пространству
Система из птождественных частиц описывается квадратично интегрируемой функцией Y п( р 1, ..., р п), симметричной (для бозонов - частиц с целым спином) или антисимметричной (для фермионов - частиц с полуцелым спином) относительно перестановки любых двух координат. Эти функции (для бозонов) принадлежат гильбертову пространству  - симметризованному тензорному произведению пэкземпляров
- симметризованному тензорному произведению пэкземпляров  Для описания систем с переменным числом частиц вводится прямая сумма пространств
Для описания систем с переменным числом частиц вводится прямая сумма пространств  - фоковское пространство
- фоковское пространство 
 Вектор W0=(l, 0, 0, ...) наз. вакуумом и интерпретируется как состояние системы без частиц. Векторы вида (0, 0, ..., Y п, 0, ...) наз. частичными векторами и отождествляются с Yn. Удобно рассматривать функции W(p)из
Вектор W0=(l, 0, 0, ...) наз. вакуумом и интерпретируется как состояние системы без частиц. Векторы вида (0, 0, ..., Y п, 0, ...) наз. частичными векторами и отождествляются с Yn. Удобно рассматривать функции W(p)из  как функции 4-вектора р=( р 0,р), где р 0=w(р). Тогда представление группы Пуанкаре U(a, А )дается формулой
как функции 4-вектора р=( р 0,р), где р 0=w(р). Тогда представление группы Пуанкаре U(a, А )дается формулой
 естественным образом индуцирует представление во всем фоковском пространстве
естественным образом индуцирует представление во всем фоковском пространстве  Генератор сдвигов вдоль оси р 0 совпадает с гамильтонианом Н 0. Здесь описано простейшее представление группы Пуанкаре, соответствующее спину s=0.
Генератор сдвигов вдоль оси р 0 совпадает с гамильтонианом Н 0. Здесь описано простейшее представление группы Пуанкаре, соответствующее спину s=0. Тогда оператор уничтожения a(f):
Тогда оператор уничтожения a(f): определяется по формуле
определяется по формуле
 - как ему сопряженный. В частности, a*(f)W0=(0, f(p),0, ...),Х т. е. оператор a*(j)рождает из вакуума частицу с волновой функцией f(p), а a(f)W0=0. Операторы рождения и уничтожения принято записывать в символическом виде
- как ему сопряженный. В частности, a*(f)W0=(0, f(p),0, ...),Х т. е. оператор a*(j)рождает из вакуума частицу с волновой функцией f(p), а a(f)W0=0. Операторы рождения и уничтожения принято записывать в символическом виде
 является для действительных
является для действительных  симметрическим оператором и наз. свободным (скалярным) квантовым полем в нулевой момент времени. Квантовое поле в момент времени х 0 имеет вид
симметрическим оператором и наз. свободным (скалярным) квантовым полем в нулевой момент времени. Квантовое поле в момент времени х 0 имеет вид


 причем
причем 
 выбирается в виде нелинейной инвариантной комбинации полей, участвующих во взаимодействии, и их производных. В простейшем случае скалярного поля, взаимодействующего с самим собой,
выбирается в виде нелинейной инвариантной комбинации полей, участвующих во взаимодействии, и их производных. В простейшем случае скалярного поля, взаимодействующего с самим собой, = -lФ 4(x). При l= 0 получается свободное поле. Взаимодействующее квантовое поле Ф(х)можно явно выразить через начальные данные Ф(x) и
= -lФ 4(x). При l= 0 получается свободное поле. Взаимодействующее квантовое поле Ф(х)можно явно выразить через начальные данные Ф(x) и 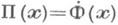 по формуле
по формуле

 выражаются через функции Грина поля Ф(х):
выражаются через функции Грина поля Ф(х):
 используя, напр., представление для Gn в виде функционального интеграла
используя, напр., представление для Gn в виде функционального интеграла

 =-lФ 4 во втором порядке по Xпропорциональна выражению
=-lФ 4 во втором порядке по Xпропорциональна выражению

 - такая функция, что Dx,e(x)- достаточно гладкая, напр., rx(x)=(1+x/х)-N, N>2 и
- такая функция, что Dx,e(x)- достаточно гладкая, напр., rx(x)=(1+x/х)-N, N>2 и  при (x,
при (x,  - называется ультрафиолетовым обрезанием). Можно считать, что лагранжиан L в (5) заменен на
- называется ультрафиолетовым обрезанием). Можно считать, что лагранжиан L в (5) заменен на
 ), что в смысле обобщенных функций существует предел
), что в смысле обобщенных функций существует предел
 +bd(х), где а и b - произвольные константы. Таким же образом регуляризуется и все выражение (6), при этом нового произвола не появляется. Аналогично регуляризуются все функции Грина во всех порядках теории возмущений по X. Подобную процедуру можно провести для
+bd(х), где а и b - произвольные константы. Таким же образом регуляризуется и все выражение (6), при этом нового произвола не появляется. Аналогично регуляризуются все функции Грина во всех порядках теории возмущений по X. Подобную процедуру можно провести для  равного любому полиному. Для
равного любому полиному. Для  процедуру регуляризации можно провести самосогласованно во всех порядках теории возмущений по Xв следующем смысле. Существуют такие константы А x, В x, С x (представимые в виде рядов по Xстепени два и выше; для их вычисления разработаны простые правила), что при подстановке в (5) вместо лагранжиана L(x) - перенормированного лагранжиана
процедуру регуляризации можно провести самосогласованно во всех порядках теории возмущений по Xв следующем смысле. Существуют такие константы А x, В x, С x (представимые в виде рядов по Xстепени два и выше; для их вычисления разработаны простые правила), что при подстановке в (5) вместо лагранжиана L(x) - перенормированного лагранжиана
 называется перенормированным лагранжианом, и говорят, что к исходному
называется перенормированным лагранжианом, и говорят, что к исходному  добавлены расходящиеся контрчлены. Эти контрчлены имеют ту же структуру, что и исходный лагранжиан (т. е. являются линейной комбинацией выражений д muдm и, u2, u4). Вследствие этого неоднозначность в величинах
добавлены расходящиеся контрчлены. Эти контрчлены имеют ту же структуру, что и исходный лагранжиан (т. е. являются линейной комбинацией выражений д muдm и, u2, u4). Вследствие этого неоднозначность в величинах  можно фиксировать, если считать заданными массу и заряд системы (масса определяется как значение р 2, при к-ром
можно фиксировать, если считать заданными массу и заряд системы (масса определяется как значение р 2, при к-ром  имеет полюс, а заряд - как значение
имеет полюс, а заряд - как значение  в нек-рой определенной точке). Анализ этой неоднозначности приводит к важному понятию ренормализационной группы [5].
в нек-рой определенной точке). Анализ этой неоднозначности приводит к важному понятию ренормализационной группы [5]. Нерешенная задача здесь - построение оболочек голоморфности
Нерешенная задача здесь - построение оболочек голоморфности  Область Dn содержит евклидовы точки вида
Область Dn содержит евклидовы точки вида 