|
"
0
C
F
G
H
K
L
N
P
S
T
W
Z
А
Б
В
Г
Д
Е
Ж
З
И
Й
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Ш
Э
Ю
Я
КВАЗИСРЕДНИХ МЕТОДЗначение КВАЗИСРЕДНИХ МЕТОД в математической энциклопедии: - конструктивная схема исследования систем со спонтанным нарушением симметрии, основанная на фундаментальной концепции квазисредних (Н. Н. Боголюбов [1], 1961). Квазисредние - термодинамические (в статистической механике) или вакуумные (в квантовой теории поля) средние от динамических величин в специальным образом модифицированной процедуре усреднения, позволяющей учесть эффекты влияния вырождения состояния системы. В статистич. механике при спонтанном нарушении симметрии на основе К. м. могут быть описаны макроскопические наблюдаемые в рамках микроскопического подхода. В задачах с вырождением одному уровню энергии отвечает более одного независимых состояний системы; среднее же значение (А)любой динамической величины Аопределенно однозначно:
где H- гамильтониан системы, b - обратная температура. Если состояние статистического равновесия системы обладает более низкой симметрией, чем гамильтониан системы (так наз. спонтанное нарушение симметрии см. [2] - [5]), то операцию усреднения (1) необходимо дополнить правилом, запрещающим "лишнее" усреднение по различным значениям рассматриваемой макроскопической величины, изменение к-рой не сопровождается изменением энергии. Это достигается введением квазисредних, т. е. средних по гамильтониану, дополненному бесконечно малыми членами, нарушающими аддитивные законы сохранения. Термодинамические средние могут оказаться неустойчивыми по отношению к такому изменению исходного гамильтониана, что и свидетельствует о вырождении состояния статистического равновесия. Итак, квазисреднее
где через Значение квазисреднего (2) может зависеть от конкретной структуры добавочного члена D Н=Нv- Н, если усредняемая динамическая величина Анеинвариантна относительно группы симметрии исходного гамильтониана Н. При стремлении параметров включения источников v к нулю произвольным образом предел обычных средних (2) для вырожденного состояния не существует. Для полного определения квазисредних необходимо указать способ стремления этих параметров к нулю, обеспечивающий сходимость (см., напр., [5]). С другой стороны, для снятия вырождения достаточно нарушить при построении Hv лишь те аддитивные законы сохранения, "выключение" к-рых приводит к неустойчивости обычных средних. При этом для квазисредних не будут выполняться именно те правила отбора корреляционных функций, к-рые обусловлены указанными законами сохранения. К. м. непосредственно связан с принципом ослабления корреляции (см. [8], [9]): корреляционные функции
где Us(xs, ts)- полевые функции в Гейзенберга представленииY(xs, ts) илиY+(xs, ts), распадаются на произведение
если совокупность точек х 1, ..., xs-1 бесконечно удаляется от совокупности точек xs, . . . , х п при фиксированных временных переменных t1, t2, ..., tn. В случае вырождения рассматриваемого состояния выражения Для построения неравновесного статистического оператора рассматриваются бесконечно малые возмущения, нарушающие симметрию ( Лиувилля уравнения )относительно обращения времени. Применение этой операции эквивалентно отбору запаздывающих решений уравнения Лиувилля (см. [7]). Вопросы о выборе способа стремления параметров включения источников v к нулю, обеспечивающего сходимость обычных средних в определении квазисредних (2) рассмотрены в рамках метода аппроксимирующих гамильтонианов, где исходный гамильтониан заменяется на специальным образом конструируемый путем замены динамических величин, коммутирующих со всей алгеброй локальных наблюдаемых в пределе большой системы, на с-числа, так наз. аппроксимирующей гамильтониан, так что этот последний гамильтониан является много проще исходного (и в широком ряде физически важных случаев допускается точное решение) и является ему эквивалентным при В рамках метода аппроксимирующих гамильтонианов указан другой альтернативный способ определения квазисредних без введения дополнительных членов в гамильтониан Н. В этом подходе при вычислении квазисреднего
Квазисредние, определенные согласно (2) и (5), совпадают. Математический аппарат К. м. включает Боголюбова теорему об особенностях типа 1/q2 и Боголюбова неравенства для Грина функций и корреляционных функций;содержит в себе алгоритмы установления нетривиальных оценок для равновесия квазисредних, позволяющих исследовать проблему упорядочения в статистич. системах и выяснять структуру энергетического спектра низколежащих возбужденных состояний (см. [4], [8]). Концепция квазисредних непосредственно связана с теорией фазовых переходов (см. [6], [7], [9]): неустойчивость термодинамических средних по отношению к возмущениям гамильтониана, нарушающим инвариантность относительно нек-рой группы преобразований, означает, что в системе происходит переход в экстремальное состояние. В квантовой теории поля для ряда модельных систем доказано наличие фазового перехода и установлена справедливость теоремы Боголюбова об особенностях типа 1/q2; исследована возможность локальной неустойчивости вакуума и появления у него доменной структуры. Лит.:[1] Боголюбов Н. Н., Избр. труды, т. 3, К., 1971; [2] Статистическая физика и квантовая теория поля, М., 1973; [3] Гриб А. А., Дамаскинский Е. В., Максимов В. М., "Успехи физ. наук", 1970, т. 102, с. 587-620; [4] Боголюбов Н. Н. (мл.), Садовников Б. И., Некоторые вопросы статистической механики, М., 1975; [5] Боголюбов Н. Н. (мл.). Метод исследования модельных гамильтонианов, М., 1974; [6] Браут Р., Фазовые переходы, пер. с англ., М., 1967; [7] Рюэль Д., Статистическая механика. Строгие результаты, пер. с англ., М., 1971; [8] Ахиезер А. И., Пелетминский С. В., Методы статистической физики, М., 1977; [9] Престон К., Гиббсовские состояния на счетных множествах, пер. с англ., М., 1977. А. Н. Ермилов, А. М. Курбатов. |
|
|
|


 динамической величины Адля системы с гамильтонианом Нопределяется как предел
динамической величины Адля системы с гамильтонианом Нопределяется как предел
 обозначено обычное среднее, взятое по гамильтониану Н v, содержащему малые нарушающие симметрию члены, вводимые параметром включения v, исчезающие при
обозначено обычное среднее, взятое по гамильтониану Н v, содержащему малые нарушающие симметрию члены, вводимые параметром включения v, исчезающие при 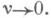 Согласно определению (2) обычное термодинамическое среднее получается дополнительным усреднением квазисреднего по группе нарушенной симметрии.
Согласно определению (2) обычное термодинамическое среднее получается дополнительным усреднением квазисреднего по группе нарушенной симметрии.

 входящие в эту формулировку, с необходимостью должны пониматься как квазисредние: приведенная выше формулировка принципа ослабления корреляций становится прямо неверной, если считать
входящие в эту формулировку, с необходимостью должны пониматься как квазисредние: приведенная выше формулировка принципа ослабления корреляций становится прямо неверной, если считать  обычными средними.
обычными средними. (см. [7]). При построении добавочного члена АН следует взять его пропорциональным решениям в общем случае минимаксной задачи для предельной
(см. [7]). При построении добавочного члена АН следует взять его пропорциональным решениям в общем случае минимаксной задачи для предельной  функции свободной энергии аппроксимирующего гамильтониана. Тогда произвольная последовательность вещественных положительных v, сходящаяся к нулю, обеспечивает сходимость в определении (2), при этом таким образом построенные квазисредние оказываются равными соответствующим решениям указанной минимаксной задачи.
функции свободной энергии аппроксимирующего гамильтониана. Тогда произвольная последовательность вещественных положительных v, сходящаяся к нулю, обеспечивает сходимость в определении (2), при этом таким образом построенные квазисредние оказываются равными соответствующим решениям указанной минимаксной задачи. рассматриваемая динамическая величина Адомножается на нек-рый, в определенном смысле стремящийся к единице при
рассматриваемая динамическая величина Адомножается на нек-рый, в определенном смысле стремящийся к единице при  множитель L, гамильтониан Ностается неизменным [4]:
множитель L, гамильтониан Ностается неизменным [4]: