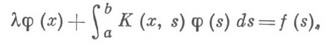|
"
0
C
F
G
H
K
L
N
P
S
T
W
Z
А
Б
В
Г
Д
Е
Ж
З
И
Й
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Ш
Э
Ю
Я
КВАДРАТУРНЫХ СУММ МЕТОДЗначение КВАДРАТУРНЫХ СУММ МЕТОД в математической энциклопедии: - метод аппроксимации интегрального оператора при построении численных методов решения интегральных уравнений. Простейший вариант К. с. м. состоит в замене интегрального оператора, напр, вида
в интегральном уравнении
на оператор с конечномерной областью значений по правилу
Интегральное уравнение в свою очередь аппроксимируется линейным алгебраич. уравнением
В правой части приближенного равенства (1) стоит квадратурная формула для интеграла по s. Возможны разнообразные обобщения аппроксимации (1) вида:
где a(N)i(x)- некоторые функции, строящиеся по ядру К( х, s). К. с. м., обобщенный в виде (2), может применяться при аппроксимации интегральных операторов с особенностями в ядре и даже сингулярных интегральных операторов. Лит.:[1] Канторович Л. В., Крылов В. И., Приближенные методы высшего анализа, 5 изд., М.- Л., 1962. А. Б. Бакушинский. |
|
|
|