|
"
0
C
F
G
H
K
L
N
P
S
T
W
Z
А
Б
В
Г
Д
Е
Ж
З
И
Й
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Ш
Э
Ю
Я
КВАДРАТУРНАЯ ФОРМУЛАЗначение КВАДРАТУРНАЯ ФОРМУЛА в математической энциклопедии: - приближенная формула для вычисления определенного интеграла:
в левой части стоит интеграл, подлежащий вычислению. Подинтегральная функция записана в виде произведения двух функций. Первая из них р(х)считается фиксированной для данной К. ф. и наз. весовой функцией, функция f(x)принадлежит достаточно широкому классу функций, напр, непрерывных и таких, что интеграл в левой части (1) существует. Сумма в правой части (1) наз. квадратурной суммой, числа xj наз. узлами К. ф., а числа С j - коэффициентами К. ф. Нахождение приближенного значения интеграла с помощью формулы (1) сводится к вычислению квадратурной суммы; при этом значения узлов и коэффициентов обычно берутся из таблиц (см., напр.. [3]). Наибольшее распространение получили К. ф., основанные на алгебраическом интерполировании. Пусть х 1,. .., xN- попарно различные точки (обычно xi
здесь Li(x)- многочлен влияния i-го узла: Li(xj) =dij(dij - символ Кронекера). Интеграл по [а, 6] от p(x)f(x)приближенно заменяется интегралом от р(х) Р{х);получается приближенное равенство вида (1), в к-ром
Существование интегралов в (2) равносильно существованию моментов весовой функции
(здесь и далее предполагается, что требуемые моменты р(х)существуют, в частности в случае р(х)=1 промежуток [ а, b]считается конечным). К. ф. (1), коэффициенты к-рой определяются равенствами (2), наз. интерполяционной. Целое число Пусть р(х)=1 и [a, b]конечен. Интерполяционная К. ф. с равноотстоящими узлами
где n - натуральное число, N=n+l, наз. Ньютона- Котеса квадратурной формулой;такая К. ф. имеет алгебраич. степень точности d=n при пнечетном и d=n+1 при пчетном. Интерполяционная К. ф. с одним узлом
наз. прямоугольников формулой, ее алгебраич. степень точности d=l, когда x=(a+b)/2, и d = 0 в остальных случаях. Пусть
Интерполяционная К. ф. (1), у к-рой узлами являются корни ортогонального на [ а, b]с весом р(х)многочлена степени N, наз. квадратурной формулой гауссова типа; ее называют также квадратурной формулой наивысшей алгебраич. степени точности, так как при условиях (4) никакая К. ф. с Nузлами не может быть точна для x2N. Наиболее употребительны К. ф. гауссова типа, к-рые определяются следующими частными случаями веса р(х) и промежутка [a, b]: вес Якоби (1-x)a(1+х)b (a>-1, b>-1), [-1, 1] при значениях параметров: а) a=b=0 (Гаусса квадратурная формула), б) вес Эрмита е -x2( вес Лагерра х a е -x(a>-1), ( Существуют К. ф., в к-рых часть узлов заранее фиксирована, а остальные узлы выбираются так, чтобы К. ф. имела наивысшую алгебраич. степень точности. Таковы, в частности, Лобатто квадратурная формула и Радо квадратурная формула для вычисления интеграла по [ - 1, 1] с весом 1. В первой из них фиксированными узлами являются -1, 1, а во второй - одна из этих точек. Две К. ф. с весом 1
наз. подобными, если tj-c=s(tj-g),Cj=sГ j, j=1, 2, ..., т, где s определяется равенством d-c'=s(d-g). В случае конечного [a, b]
где х i определяются равенствами (3). Если для вычисления интегралов по промежуткам [х;, х i+1]применяются К. ф., подобные одной и той же К. ф., то равенст- {5) приведет к составной К. ф. для вычисления интеграла, стоящего в левой его части. Такова, напр., составная К. ф. прямоугольников:
В случае b-a=2p эта К. ф. точна для cos kx,sin kx при k = 0,1, . . ., n-1. Можно рассматривать интерполяционные К. ф., к-рые получаются интегрированием интерполяционного многочлена Эрмита функции f(x). В квадратурную сумму такой К. ф. входит не только значение самой функции в узле, но и значения ее последовательных производных до нек-рого порядка. Значение производных подинтегральной функции на концах промежутка интегрирования используются и в Эйлера- Маклорена формуле. Для погрешности К. ф. (1)
имеются представления, в к-рые входит производная f(r)(x). Эти представления мало пригодны для фактической оценки R(f), так как при этом требуется оценка производной f(r)(x). Погрешность R(f) является аддитивным и однородным функционалом на векторном пространстве функций, для к-рых она определена. Другой подход основан на минимизации нормы функционала погрешности R(f) построению К. ф. Пусть R(f) - погрешность К. ф., к-рая точна для всех многочленов степени не выше r-1, при этом [ а, b]= [0, 1] и р(х)=1, и W(r)q(q>1, r- натуральное число) - векторное пространство функций f(x), к-рые на (0, 1] имеют абсолютно непрерывную производную порядка r-1 и суммируемую со степенью qпроизводную порядка r. Две функции из W{r)q считают эквивалентными, если их разность есть многочлен степени не выше r-1. Множество классов эквивалентности (факторпространство W(r)q по векторному пространству многочленов степени не выше r-1) является векторным пространством, к-рое обозначают
где f - любая функция, принадлежащая г|5. Функционал погрешности К. ф. рассматривают на
к-рое является точным. Ясно, что ||R|| есть функция параметров х k, с k, k=i,2, ..., N, К. ф., и естественно -пытаться их выбрать так, чтобы ||R|| принимала наименьшее значение. Это приводит к такой К. ф. (из класса рассматриваемых), погрешность к-рой имеет минимальную оценку для всех функций пространства W(r)q. Таким образом, построение К. ф. сводится к решению экстремальной задачи. Эта задача уже в рассмотренном частном случае весьма сложна и ее решение получено (1978) лишь при r=1 и r=2. Лит.:[1] Крылов В. И., Приближенное вычисление интегралов, 2 изд., М., 1967; [2] Никольский С. М., Квадратурные формулы, 2 изд., М., 1974; [3] Крылов В. И., Шульгина Л. Т., Справочная книга по численному интегрированию, М., 1966. И. П. Мысовских. |
|
|
|


 [a,b], хотя это требование не является обязательным) и Р(х)- интерполяционный многочлен функции f(x), построенный по ее значениям в этих точках:
[a,b], хотя это требование не является обязательным) и Р(х)- интерполяционный многочлен функции f(x), построенный по ее значениям в этих точках:


 наз. алгебраической степенью точности К. ф. (1), если эта формула точна, когда f(x)- любой многочлен степени выше d, и не точна для f(x)=xd+1. Чтобы К. ф. (1) была интерполяционной, необходимо и достаточно, чтобы для ее алгебраич. степени точности dвыполнялось неравенство
наз. алгебраической степенью точности К. ф. (1), если эта формула точна, когда f(x)- любой многочлен степени выше d, и не точна для f(x)=xd+1. Чтобы К. ф. (1) была интерполяционной, необходимо и достаточно, чтобы для ее алгебраич. степени точности dвыполнялось неравенство 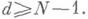



 ( Мелера квадратурная формула), в) a=b=
( Мелера квадратурная формула), в) a=b= , г)
, г)
 ' );
' ); ).
).



 В
В  можно ввести норму, полагая для класса
можно ввести норму, полагая для класса 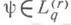

 полагая R(y)=R(f),
полагая R(y)=R(f), Функционал R(y) непрерывен в линейном нормированном пространстве
Функционал R(y) непрерывен в линейном нормированном пространстве  Его норма ||R|| характеризует точность К. ф. для всех функций из
Его норма ||R|| характеризует точность К. ф. для всех функций из  для любой
для любой  справедливо неравенство
справедливо неравенство