|
"
0
C
F
G
H
K
L
N
P
S
T
W
Z
А
Б
В
Г
Д
Е
Ж
З
И
Й
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Ш
Э
Ю
Я
КАТЕГОРИЯ С ИНВОЛЮЦИЕЙЗначение КАТЕГОРИЯ С ИНВОЛЮЦИЕЙ в математической энциклопедии: - категория, обладающая рядом характерных свойств категории бинарных отношений. К. с и. наз. категория, в к-рой каждое множество Н( А, В )частично упорядочено отношением
В каждой К. с и. утверждение, двойственное истинному утверждению, также истинно (усиленный принцип двойственности). Категория, двойственная К. с и., является К. с и. Всякая группа может рассматриваться как К. с п., состоящая из одного объекта, если в качестве отношения порядка взять отношение тождества (тривиальный частичный порядок), а в качестве инволюции - отображение, сопоставляющее элементу группы обратный к нему элемент. Важный пример К. с и.- категория бинарных отношений Описание строения разных классов К. с п., их связей с классами точных, абелевых, регулярных категорий и их использование в гомологич. алгебре можно найти в [1] - [4]. Лит.:[1] Brinkmann Н. В., Рирре D., Abelsche und exakte Kategorien, В. - Hdlb.-N. Y., 1969; [2] Кawahara J., "Memoirs Fac. Sci., Kyushu Univ. Ser. A. Math.", 1973, v. 27, № 1, p. 149-73; [3] его жe, там же, 1973, v. 27, №2, p. 249-73; [4] Цаленко М. Ш., "Докл. АН СССР", 1973, т. 211, № 2, с. 297-9. М. Ш. Цаленко. |
|
|
|
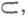а также задано отображение 
наз. инволюцией, сопоставляющее морфизму а морфизм 
и удовлетворяющее следующим условиям: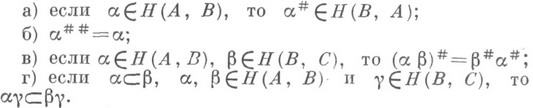
над категорией множеств 
строится следующим образом.
морфизмы 
- бинарные отношения с обычным умножением бинарных отношений и частичной упорядоченностью, индуцируемой отношением включения подмножеств декартова произведения. Инволюция в этой категории определяется с помощью перестановки множителей в декартовом произведении. Аналогично можно построить категории бинарных отношений над категориями групп, колец, топологич. групп и т. п. Однако для категории, всех топологич. пространств описанное выше построение зависит от выбора структуры бикатегории и может привести к неассоциативному умножению.