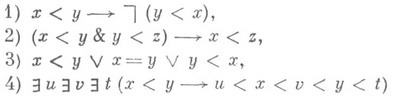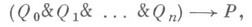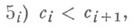КАТЕГОРИЧНОСТЬ В МОЩНОСТИ

Значение КАТЕГОРИЧНОСТЬ В МОЩНОСТИ в математической энциклопедии:

x - свойство класса алгебраич. систем, заключающееся в изоморфизме всех систем из этого класса, имеющих мощность x. Теория Т1-го порядка наз. категоричной в мощности х, если все модели Тмощности xизоморфны одной алгебраич. системе. Счетная полная теория Ткатегорична в счетной мощности тогда и только тогда, когда для любого натурального числа псуществует такое конечное множество F_n формул сигнатуры Тсо свободными переменными x_l, . .., x_m что любая формула сигнатуры Тсо свободными переменными х ₁,..., х _п эквлвалентна в теории Тодной из формул множества F_n. Совокупность аксиом:

определяет теорию Т ₀ плотных линейных порядков, к-рая категорична в счетной мощности и не категорична во всех несчетных мощностях. Теория Т ₁ алгебраически замкнутых полей характеристики 0 категорична во всех несчетных мощностях, но не категорична в счетной мощности. Верна общая теорема: если счетная теория Т1-го порядка категорична в какой-нибудь несчетной мощности, то она категорична во всех несчетных мощностях. Этот результат обобщен на несчетные теории Тс заменой в условии несчетных мощностей на мощности, большие мощности теории Т. Квазитождеством наз. универсальное замыкание формулы

где Q_i и Р - атомарные формулы. В счетных теориях T', аксиоматизируемых с помощью квазитождеств, возможностей распределения категоричности еще меньше: если такая теория T' категорична в счетной мощности, то она категорична во всех мощностях. Если к аксиомам теории Т ₀ добавить аксиомы для констант с,-

где iпробегает все натуральные числа, то полученная теория Т ₃ имеет ровно три счетных модели (с точностью до изоморфизма), так как возможны лишь 3 случая: множество {с ₀, с ₁, ..., с _п, ...} не имеет верхней грани, имеет верхнюю грань, но не имеет наименьшей верхней грани, и, наконец, имеет наименьшую верхнюю грань. Если в счетных моделях М ₁ и М ₂ теории T₃ имеет место один и тот же из описанных случаев, то М ₁ изоморфна М ₂. Оказывается, что среди теорий, категоричных в несчетных мощностях, аналогичного примера найти нельзя. А именно: если теория Т1-го порядка категорична в несчетной мощности, то число счетных моделей Т(с точностью до изоморфизма) либо равно 1, либо бесконечно.

Лит.:[1] Сакс Дж., Теория насыщенных моделей, пер. с англ., М., 1976; [2] Палютин Е. А., "Алгебра и логика", 1975, т. 14, №2, с. 145-85; [3] Shelah S., "Proc. of Symp. Pure Math.", 1974, v. 13, № 2, p. 187-203.

E. А. Палютин.