"
0
C
F
G
H
K
L
N
P
S
T
W
Z
А
Б
В
Г
Д
Е
Ж
З
И
Й
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Ш
Э
Ю
Я
АНАЛИТИЧЕСКОЕ ПРОДОЛЖЕНИЕ
Значение АНАЛИТИЧЕСКОЕ ПРОДОЛЖЕНИЕ в математической энциклопедии:
функции- доопределение функции f0, определенной на нек-ром подмножестве Екомплексного многообразия М, до функции f, голоморфной в нек-рой области  , содержащей Е, такое, что сужение
, содержащей Е, такое, что сужение  функции f на Есовпадает с
функции f на Есовпадает с  . Отправным в теории А. п. является понятие (аналитического) элемента, т. е. пары
. Отправным в теории А. п. является понятие (аналитического) элемента, т. е. пары  , где
, где  - область на Ми f - голоморфная в Dфункция. Говорят, что элементы
- область на Ми f - голоморфная в Dфункция. Говорят, что элементы  составляют непосредственное А. п. друг друга через связную компоненту
составляют непосредственное А. п. друг друга через связную компоненту 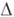 множества
множества  если
если  Элемент
Элемент 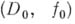 , по определению, аналитически продолжается в граничную точку
, по определению, аналитически продолжается в граничную точку  если существует непосредственное_А. п.
если существует непосредственное_А. п.  элемента
элемента  через
через  такое, что
такое, что 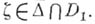 Максимальным (в М).А. п.
Максимальным (в М).А. п. 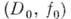 наз. элемент (D,/), аналитически продолжающий
наз. элемент (D,/), аналитически продолжающий  в область
в область  но не продолжаемый аналитически ни в одну граничную точку D. Максимальное А. п.
но не продолжаемый аналитически ни в одну граничную точку D. Максимальное А. п.  в Мединственно, но не всегда существует. Для устранения этого недостатка вводятся области наложения над М(римановы поверхности в случае
в Мединственно, но не всегда существует. Для устранения этого недостатка вводятся области наложения над М(римановы поверхности в случае  ), к-рые строятся из элементов, аналитически продолжающих
), к-рые строятся из элементов, аналитически продолжающих  Элемент
Элемент  наз. А. п. элемента
наз. А. п. элемента  , если существует конечный набор элементов
, если существует конечный набор элементов 
 и связных компонент А,- соответственно в
и связных компонент А,- соответственно в  таких, что
таких, что  являются непосредственными А. п. друг друга через Д,-. Говорят, что голоморфная функция
являются непосредственными А. п. друг друга через Д,-. Говорят, что голоморфная функция  , определенная первоначально в области
, определенная первоначально в области  , аналитически продолжается в точку
, аналитически продолжается в точку  , если существует А. п.
, если существует А. п. элемента
элемента 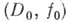 такое, что
такое, что  . Среди элементов, продолжающих
. Среди элементов, продолжающих  в точку z, вводится отношение эквивалентности:
в точку z, вводится отношение эквивалентности: 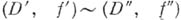 , если
, если  в окрестности z. На Множестве классов эквивалентности
в окрестности z. На Множестве классов эквивалентности  (для всех возможных z) естественно вводится топология и комплексная структура области наложения над М. Функция
(для всех возможных z) естественно вводится топология и комплексная структура области наложения над М. Функция  естественно поднимается в
естественно поднимается в  (значение на классе эквивалентности в z, содержащем
(значение на классе эквивалентности в z, содержащем 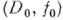 , полагаем равным
, полагаем равным  ), аналитически продолжается на всю D f и в определенном смысле не продолжается ни в одну граничную точку
), аналитически продолжается на всю D f и в определенном смысле не продолжается ни в одну граничную точку  над
над  .
.
В случае, когда 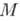 есть комплексная плоскость
есть комплексная плоскость  или, более общо, комплексное пространство
или, более общо, комплексное пространство  ,
,  , этот процесс А. п. описывается проще. Каноническим элементом наз. пара
, этот процесс А. п. описывается проще. Каноническим элементом наз. пара  , где
, где  - степенной ряд с центром в точке ас непустой областью сходимости Da. Канонич. элемент
- степенной ряд с центром в точке ас непустой областью сходимости Da. Канонич. элемент  вдоль пути
вдоль пути  если существует семейство канонич. элементов
если существует семейство канонич. элементов 
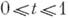 , с центрами
, с центрами  таких, что
таких, что 
 и для каждого
и для каждого  элементы
элементы  являются непосредственными А. п.
являются непосредственными А. п. 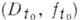 для всех t, достаточно близких к
для всех t, достаточно близких к  . Семейство
. Семейство  на самом деле определяется однозначно. Если
на самом деле определяется однозначно. Если  ,
,  , есть непрерывное семейство путей в
, есть непрерывное семейство путей в  с общими концами аи b и если
с общими концами аи b и если  аналитически продолжается вдоль каждого
аналитически продолжается вдоль каждого  , то результат
, то результат  не зависит от
не зависит от  (монодромии теорема). Точками
(монодромии теорема). Точками  в случае
в случае  являются канонич. элементы
являются канонич. элементы 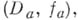 получаемые посредством А. п. вдоль всевозможных путей в
получаемые посредством А. п. вдоль всевозможных путей в  ;
;  поднимается в
поднимается в  аналитически на всю до голоморфной функции
аналитически на всю до голоморфной функции  , причем
, причем  есть область
есть область  голоморфности
голоморфности 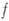 .
.
Описанный общий процесс А. п. практически малоэффективен, поэтому в анализе используется много специальных методов А. п. Сюда относятся различные аиалитич. представления: интегралы, зависящие от параметра [интеграл типа Коши (см. Коши интеграл), Лапласа интеграл, интеграл Бореля (см. Бореля преобразование).и др.], замена переменного в степенном ряде, специальные способы суммирования степенных рядов [разложение Бореля в ряд многочленов, сходящийся в максимальном полигоне (см. Бореля метод суммирования), ряд Миттаг-Леффлера, сходящийся в максимальной звезде (см. Звезда элемента функции, Миттаг-Леффлера метод суммирования).и др.], принцип симметрии Римана - Шварца (см. Римана- Шварца принцип), функциональные и дифференциальные уравнения, определяющие функцию (напр., уравнение  для гамма-функции, условия периодичности, четности, симметрии и т. п.), аналитич. выражения через известные функции.
для гамма-функции, условия периодичности, четности, симметрии и т. п.), аналитич. выражения через известные функции.
К теме А. п. относятся также исследования о связи между исходным элементом аналитич. функции (рядом Тейлора) и свойствами полной аналитической функции, порождаемой этим элементом (см. [1]); результаты об особых точках (критерии особых точек, Адамара теорема мультипликационная, Фабри теорема об отношении) и особых линиях (теоремы о лакунах и непродолжаемости за границу круга сходимости, напр. Адамара теорема о лакунах, Фабри теорема о лакунах и др.), теоремы о сверхсходимости и о связях А. п. степенного ряда со свойствами целой функции, определяющей его коэффициенты, вопросы мероморфного продолжения, мероморфное продолжение при помощи Паде аппроксимаций и др. К А. п. следует отнести и теоремы об устранении особенностей (устранение изолированной особенности ограниченной голоморфной функции, устранение спрямляемых разрезов при условии непрерывности и т. п.), а также большой класс теорем об одновременном продолжении голоморфных функций многих комплексных переменных. В  при
при  имеются области, из к-рых любая голоморфная функция продолжается в более широкую область (в одномерном случае такого явления нет). Поэтому важной задачей А. п. функций многих комплексных переменных является описание этих более широких областей - так наз. голоморфных расширений, напр, известны описания голоморфности оболочек для Гартогса областей, л-круговых и трубчатых областей, теоремы об устранении компактных особенностей и особенностей коразмерности
имеются области, из к-рых любая голоморфная функция продолжается в более широкую область (в одномерном случае такого явления нет). Поэтому важной задачей А. п. функций многих комплексных переменных является описание этих более широких областей - так наз. голоморфных расширений, напр, известны описания голоморфности оболочек для Гартогса областей, л-круговых и трубчатых областей, теоремы об устранении компактных особенностей и особенностей коразмерности  Боголюбова теорема"острие клина" н теорема В. С. Владимирова о С-выпуклой оболочке (см. [3]). Известно несколько эффективных методов построения голоморфного расширения областей (см. [3]).
Боголюбова теорема"острие клина" н теорема В. С. Владимирова о С-выпуклой оболочке (см. [3]). Известно несколько эффективных методов построения голоморфного расширения областей (см. [3]).
А. п. функций действительного переменного сводится к А. п. голоморфных функций, т. к. для любой области  и любой функции
и любой функции 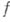 , аналитической в
, аналитической в  , найдутся область
, найдутся область  и голоморфная в
и голоморфная в  функция
функция  такие, что
такие, что 
Лит.:[1] Бибербах Л., Аналитическое продолжение, пер. с нем., М., 1967; [2] Маркушевич А. И., Теория аналитических функций, 2 изд., т. 2, М., 1968; [3] Владимиров В С Методы теории функций многих комплексных переменных, М., 1964. Е. М. Чирка.

 , содержащей Е, такое, что сужение
, содержащей Е, такое, что сужение  функции f на Есовпадает с
функции f на Есовпадает с  . Отправным в теории А. п. является понятие (аналитического) элемента, т. е. пары
. Отправным в теории А. п. является понятие (аналитического) элемента, т. е. пары  , где
, где  - область на Ми f - голоморфная в Dфункция. Говорят, что элементы
- область на Ми f - голоморфная в Dфункция. Говорят, что элементы  составляют непосредственное А. п. друг друга через связную компоненту
составляют непосредственное А. п. друг друга через связную компоненту 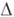 множества
множества  если
если  Элемент
Элемент 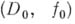 , по определению, аналитически продолжается в граничную точку
, по определению, аналитически продолжается в граничную точку  если существует непосредственное_А. п.
если существует непосредственное_А. п.  элемента
элемента  через
через  такое, что
такое, что 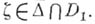 Максимальным (в М).А. п.
Максимальным (в М).А. п. 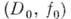 наз. элемент (D,/), аналитически продолжающий
наз. элемент (D,/), аналитически продолжающий  в область
в область  но не продолжаемый аналитически ни в одну граничную точку D. Максимальное А. п.
но не продолжаемый аналитически ни в одну граничную точку D. Максимальное А. п.  в Мединственно, но не всегда существует. Для устранения этого недостатка вводятся области наложения над М(римановы поверхности в случае
в Мединственно, но не всегда существует. Для устранения этого недостатка вводятся области наложения над М(римановы поверхности в случае  ), к-рые строятся из элементов, аналитически продолжающих
), к-рые строятся из элементов, аналитически продолжающих  Элемент
Элемент  наз. А. п. элемента
наз. А. п. элемента  , если существует конечный набор элементов
, если существует конечный набор элементов 
 и связных компонент А,- соответственно в
и связных компонент А,- соответственно в  таких, что
таких, что  являются непосредственными А. п. друг друга через Д,-. Говорят, что голоморфная функция
являются непосредственными А. п. друг друга через Д,-. Говорят, что голоморфная функция  , определенная первоначально в области
, определенная первоначально в области  , аналитически продолжается в точку
, аналитически продолжается в точку  , если существует А. п.
, если существует А. п. элемента
элемента 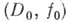 такое, что
такое, что  . Среди элементов, продолжающих
. Среди элементов, продолжающих  в точку z, вводится отношение эквивалентности:
в точку z, вводится отношение эквивалентности: 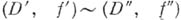 , если
, если  в окрестности z. На Множестве классов эквивалентности
в окрестности z. На Множестве классов эквивалентности  (для всех возможных z) естественно вводится топология и комплексная структура области наложения над М. Функция
(для всех возможных z) естественно вводится топология и комплексная структура области наложения над М. Функция  естественно поднимается в
естественно поднимается в  (значение на классе эквивалентности в z, содержащем
(значение на классе эквивалентности в z, содержащем 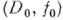 , полагаем равным
, полагаем равным  ), аналитически продолжается на всю D f и в определенном смысле не продолжается ни в одну граничную точку
), аналитически продолжается на всю D f и в определенном смысле не продолжается ни в одну граничную точку  над
над  .
.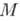 есть комплексная плоскость
есть комплексная плоскость  или, более общо, комплексное пространство
или, более общо, комплексное пространство  ,
,  , этот процесс А. п. описывается проще. Каноническим элементом наз. пара
, этот процесс А. п. описывается проще. Каноническим элементом наз. пара  , где
, где  - степенной ряд с центром в точке ас непустой областью сходимости Da. Канонич. элемент
- степенной ряд с центром в точке ас непустой областью сходимости Da. Канонич. элемент  вдоль пути
вдоль пути  если существует семейство канонич. элементов
если существует семейство канонич. элементов 
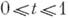 , с центрами
, с центрами  таких, что
таких, что 
 и для каждого
и для каждого  элементы
элементы  являются непосредственными А. п.
являются непосредственными А. п. 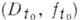 для всех t, достаточно близких к
для всех t, достаточно близких к  . Семейство
. Семейство  на самом деле определяется однозначно. Если
на самом деле определяется однозначно. Если  ,
,  , есть непрерывное семейство путей в
, есть непрерывное семейство путей в  с общими концами аи b и если
с общими концами аи b и если  аналитически продолжается вдоль каждого
аналитически продолжается вдоль каждого  , то результат
, то результат  не зависит от
не зависит от  (монодромии теорема). Точками
(монодромии теорема). Точками  в случае
в случае  являются канонич. элементы
являются канонич. элементы 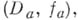 получаемые посредством А. п. вдоль всевозможных путей в
получаемые посредством А. п. вдоль всевозможных путей в  ;
;  поднимается в
поднимается в  аналитически на всю до голоморфной функции
аналитически на всю до голоморфной функции  , причем
, причем  есть область
есть область  голоморфности
голоморфности 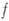 .
. для гамма-функции, условия периодичности, четности, симметрии и т. п.), аналитич. выражения через известные функции.
для гамма-функции, условия периодичности, четности, симметрии и т. п.), аналитич. выражения через известные функции. при
при  имеются области, из к-рых любая голоморфная функция продолжается в более широкую область (в одномерном случае такого явления нет). Поэтому важной задачей А. п. функций многих комплексных переменных является описание этих более широких областей - так наз. голоморфных расширений, напр, известны описания голоморфности оболочек для Гартогса областей, л-круговых и трубчатых областей, теоремы об устранении компактных особенностей и особенностей коразмерности
имеются области, из к-рых любая голоморфная функция продолжается в более широкую область (в одномерном случае такого явления нет). Поэтому важной задачей А. п. функций многих комплексных переменных является описание этих более широких областей - так наз. голоморфных расширений, напр, известны описания голоморфности оболочек для Гартогса областей, л-круговых и трубчатых областей, теоремы об устранении компактных особенностей и особенностей коразмерности  Боголюбова теорема"острие клина" н теорема В. С. Владимирова о С-выпуклой оболочке (см. [3]). Известно несколько эффективных методов построения голоморфного расширения областей (см. [3]).
Боголюбова теорема"острие клина" н теорема В. С. Владимирова о С-выпуклой оболочке (см. [3]). Известно несколько эффективных методов построения голоморфного расширения областей (см. [3]). и любой функции
и любой функции 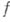 , аналитической в
, аналитической в  , найдутся область
, найдутся область  и голоморфная в
и голоморфная в  функция
функция  такие, что
такие, что 