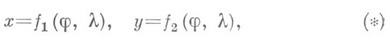КАРТОГРАФИЧЕСКАЯ ПРОЕКЦИЯ

Значение КАРТОГРАФИЧЕСКАЯ ПРОЕКЦИЯ в математической энциклопедии:

- отображение всей поверхности земного эллипсоида или какой-либо ее части на плоскость, получаемое в основном с целью построения карты.

К. п. чертят в определенном масштабе. Уменьшая мысленно земной эллипсоид в Мраз, получают его геометрич. модель - глобус, изображение к-рого в натуральную величину на плоскости дает карту поверхности этого эллипсоида. Величина 1 : Мопределяет главный, или общий, масштаб карты. Однако основной характеристикой К. п. в любой ее точке является частный масштаб m. Это - величина, обратная отношению бесконечно малого отрезка dS на земном эллипсоиде к его изображению da на плоскости: 1/m=dS/ds, причем mзависит от положения точки на эллипсоиде и от направления выбранного отрезка. Отношение m/M наз. относительным масштабом, или увеличением длины, разность (m/M-1) - искажением длины. Численное значение главного масштаба Мучитывается только при вычислениях координат точек К. п. и при использовании карты, а при исследованиях К. п. полагают M=l.

В картографии часто ограничиваются рассмотрением отображений на плоскость сферы нек-рого радиуса R, отклонениями к-рой от земного эллипсоида можно пренебречь или каким-либо способом их учесть. Поэтому далее имеются в виду отображения на плоскость хОу сферы, отнесенной к географич. координатам j (широта) и X(долгота).

Уравнения К. п. имеют вид

где f₁ и f₂ - функции, удовлетворяющие нек-рым общим условиям (К. п. может быть определена также уравнениями, в к-рых фигурируют не прямоугольные координаты плоскости х, у, а какие-либо иные). Изображения меридианов l=const и параллелей j=const в данной К. п. образуют картографическую сетку.

КАРТОГРАФИЧЕСКИЕ ПРОЕКЦИИ

1. СЕТИ СФЕРИЧЕСКИХ КООРДИНАТНЫХ ЛИНИЙ

2. ШАР И ЕГО ОРТОГРАФИЧЕСКИЕ ПРОЕКЦИИ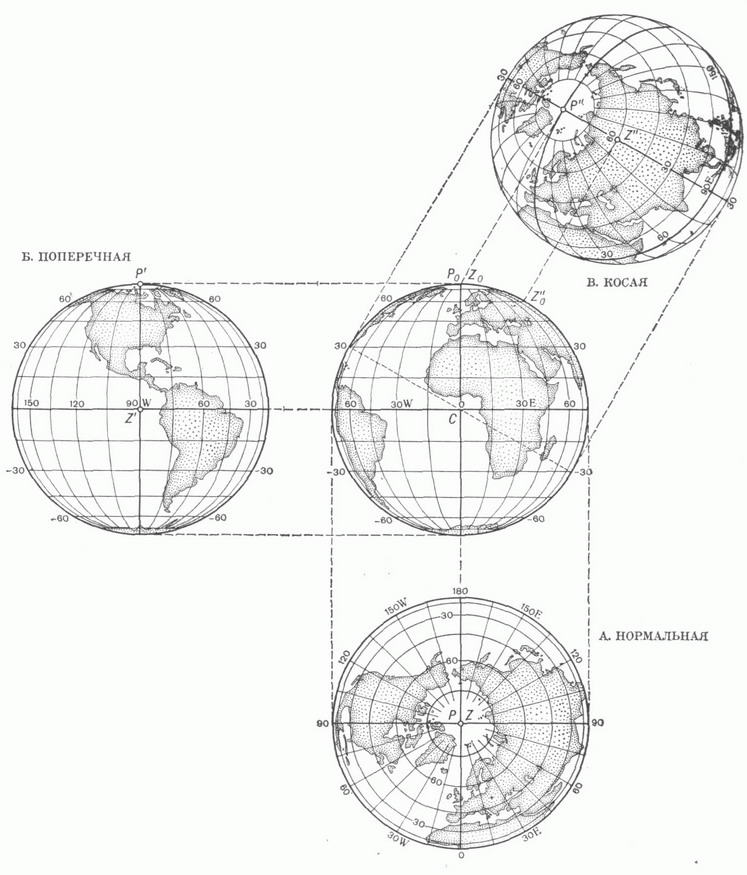

3. ЦИЛИНДРИЧЕСКИЕ ' ПРОЕКЦИИ

А. РАВНОУГОЛЬНАЯ МЕРКАТОРА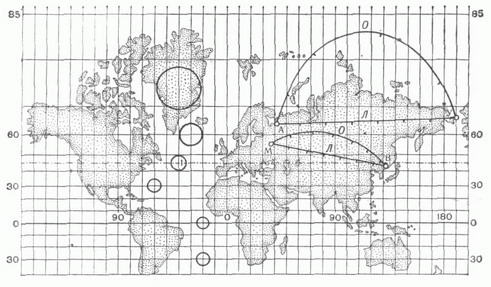

Б. РАВНОПРОМЕЖУТОЧНАЯ (ПРЯМОУГОЛЬНАЯ)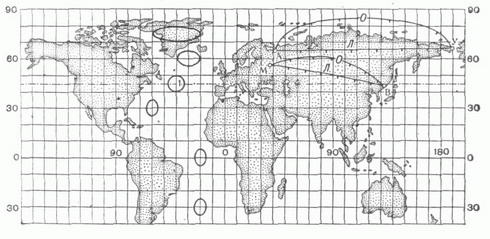

В. РАВНОВЕЛИКАЯ (ИЗОЦИЛИНДРИЧЕСКАЯ)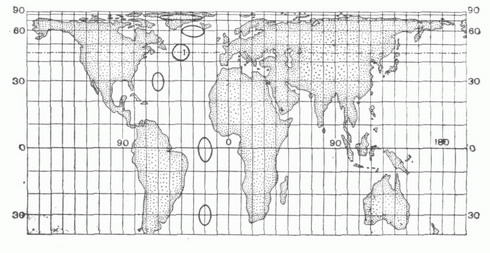

4. КОНИЧЕСКИЕ ПРОЕКЦИИ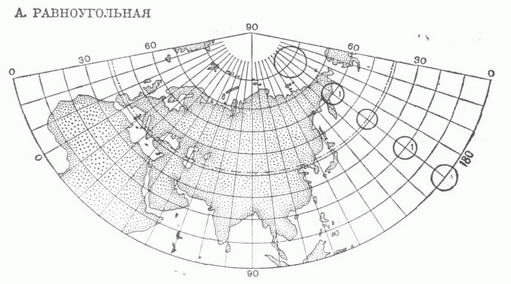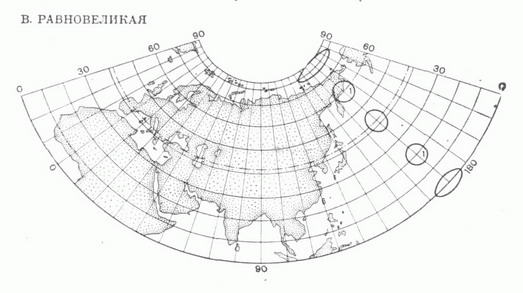

5. АЗИМУТАЛЬНЫЕ ПРОЕКЦИИ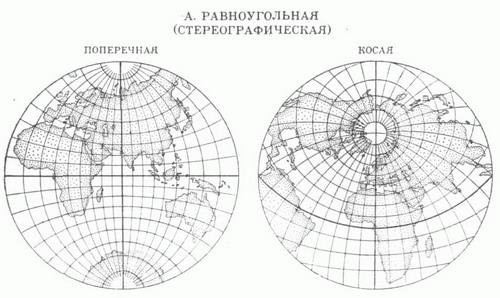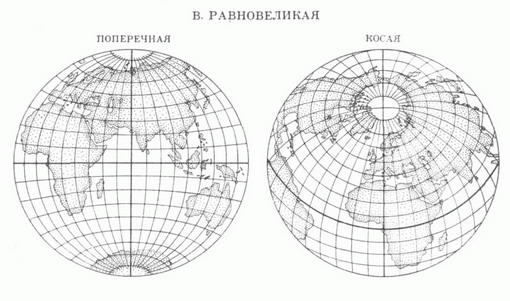

6. ПСЕВДОКОНИЧЕСКАЯ РАВНОВЕЛИКАЯ ПРОЕКЦИЯ БОННА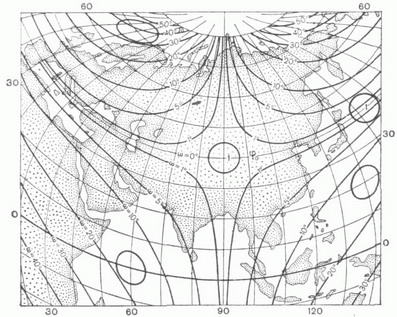

7. КОСАЯ ПЕРСПЕКТИВНО-ЦИЛИНДРИЧЕСКАЯ ПРОЕКЦИЯ М. <Д. СОЛОВЬЕВА

8. ПСЕВДОЦИЛИНДРИЧЕСКИЕ ПРОЕКЦИИ

9. ПОЛИКОНИЧЕСКИЕ ПРОЕКЦИИ

При картографировании областей, содержащих география, полюсы, иногда применяют не географии, координаты, а другие, в к-рых полюсы оказываются обыкновенными точками координации. Напр., используют сферич. координаты, координатные линии к-рых- так наз. вертикалы (условная долгота на них a=const) и альмукантараты (где полярные расстояния z=const)-аналогичны географич. меридианам и параллелям, но их полюс Z₀(j₀, l₀) не совпадает с географич. полюсом Р ₀ (рис. 1). Всякая К. п., данная уравнениями (*), наз. нормальной, или прямой (j₀=p/2). Если та же самая проекция сферы вычисляется по формулам (*), в к-рых вместо ср, Кфигурируют z, а, то эта проекция наз. поперечной при j₀=0, и косой, если 0<j₀<p/2. На рис. 2 показаны нормальная (А), поперечная (Б) и косая (В) ортографич. проекции шара.

Искажения в бесконечно малой области около какой-либо точки проекции подчиняются нёк-рым общим законам. Во всякой точке карты, составленной в проекции, не являющейся равноугольной (см. ниже), существует два таких взаимно перпендикулярных направления, к-рым на отображаемой поверхности соответствуют также взаимно перпендикулярные направления- так наз. главные направления отображения. Масштабы по этим направлениям имеют экстремальные значения m_max=a и m_min=b. Если в какой-либо К. п. изображения меридианов и параллелей пересекаются под прямым углом, то их направления и есть главные для данной К. п. Искажения длин в данной точке К. п. наглядно представляет эллипс искажений, подобный и подобно расположенный изображению бесконечно малой окружности, описанной вокруг соответствующей точки отображаемой поверхности. Полудиаметры этого эллипса численно равны частным масштабам в данной точке в соответствующих направлениях, полуоси эллипса равны экстремальным масштабам, а направления их - главные.

В равноугольных (конформных) К. п. масштаб зависит только от положения точки и не зависит от направления. Эллипсы искажения - окружности. Примеры: проекция Меркатора, стереографическая проекция, равноугольная коническая проекция и др. (см. рис. 3А, 5А, 4А).

В равновеликих (эквивалентных) К. п. сохраняются площади; точнее, площади фигур на картах, составленных в таких проекциях, пропорциональны площадям соответствующих фигур в натуре, причем коэффициент пропорциональности - величина, обратная квадрату главного масштаба карты. Эллипсы искажений всюду имеют одинаковую площадь, различаясь формой и ориентировкой; см., например, рис. ЗВ, 4В, 5В.

Произвольные К. п. (см., напр., рис. 7) не относятся ни к равноугольным, ни к равновеликим. Из них выделяют равнопромежуточные, в к-рых один из главных масштабов равен единице (см. рис. ЗБ, 4Б, 5Б), и ортодро ми чески е, в к-рых большие круги сферы (ортодромы) изображаются прямыми.

При изображении сферы на плоскости свойства равноугольности, равновеликости; равнопромежуточности и ортодромичности несовместимы.

Для показа искажений в разных местах изображаемой области применяют: эллипсы искажений (см., напр., рис. 3,4); изоколы - линии равного значения искажений (на рис. 8 В см. изоколы наибольшего искажения углов и и изоколы масштаба площадей р);изображения в нек-рых местах карты нек-рых сферич., линий, обычно ортодромий "О" и изогональных траекторий меридианов-локсодромий "Л" (см., напр., рис. 3А, 3Б).

По виду картографической сетки К. п. подразделяют на следующие группы.

Цилиндрические проекции - проекции, в к-рых меридианы изображаются равноотстоящими параллельными прямыми, а параллели - прямыми, перпендикулярными меридианам (см. рис. 3).

Конические проекции - проекции, в к-рых параллели изображаются концентрич. окружностями, меридианы - ортогональными им прямыми, причем углы между последними пропорциональны соответствующим разностям долгот (см. рис. 4).

Азимутальные проекции - проекции, в к-рых параллели изображаются концентрич. окружностями, меридианы - их радиусами, при этом углы между последними равны соответствующим разностям долгот (см. рис. 5).

Псевдоконические проекции - проекции, в к-рых параллели изображаются концентрич. окружностями, средний меридутн - прямой линией, остальные меридианы - кривыми симметричными относительно изображения среднего меридиана (см.,напр., рис. 6).

Псевдоцплиндрические проекции - проекции, в к-рых параллели изображаются параллельными прямыми, средний меридиан - прямой линией, перпендикулярной этим прямым, остальные меридианы - кривыми (см. рис. 8).

Пол и конические проекции - проекции, в к-рых параллели изображаются окружностями с центрами, расположенными на одной прямой, изображающей средний меридиан, остальные меридианы - кривыми, также симметричными относительно этой прямой (см. рис. 9). При построении конкретных поликонических проекций ставятся дополнительные условия.

Существуют и другие проекции, не относящиеся к указанным видам. Цилиндрические, конические и азимутальные проекции, называемые простейшими, часто относят к круговым проекциям в широком смысле, выделяя из них круговые проекции в узком смысле- проекции, в к-рых все меридианы и параллели изображаются окружностями.

Об использовании, выборе, исследованиях свойств, преобразованиях К. п. см. статью Картографии мате матические задачи и лит. при ней. Г. А. Мещеряков.