"
0
C
F
G
H
K
L
N
P
S
T
W
Z
А
Б
В
Г
Д
Е
Ж
З
И
Й
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Ш
Э
Ю
Я
КАРТАНА - ВЕЙЛЯ БАЗИС
Значение КАРТАНА - ВЕЙЛЯ БАЗИС в математической энциклопедии:
конечномерной полупростой комплексной алгебры Ли g - базис g, составленный из элементов Картана подалгебры алгебры g и корневых векторов Х a, где D - система всех ненулевых корней алгебры g относительно т. К.- В. б. выбирается неоднозначно. Корень a(h),
где D - система всех ненулевых корней алгебры g относительно т. К.- В. б. выбирается неоднозначно. Корень a(h), 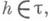 . как линейная форма над т, отождествляется с вектором
. как линейная форма над т, отождествляется с вектором 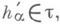 для которого
для которого 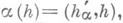
где ( х, у)- Киллинга форма в алгебре д. При этом
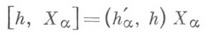
для всякого 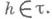 Еслито
Еслито  причем
причем 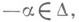 можно выбрать Х a. так, чтобы выполнялось равенство [Х a, X-a] = h'a. Если
можно выбрать Х a. так, чтобы выполнялось равенство [Х a, X-a] = h'a. Если  то
то
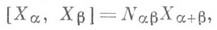
где 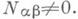 Если а, Р,
Если а, Р, a+b+g=0, то Nab=Nrg=Nga. Существует нормировка векторов Х а, при которой Nab=-N-a,-b, причем числа Nab получаются рациональными. Существует нормировка векторов Х a, при которой все Nab - целые (см. Шевалле группа). Определение К.- В. б. (введенное Г. Вейлем в [1]), а также все сказанное выше о векторах Х a, h'a. и числах Nab. дословно переносится на случай произвольной конечномерной полупростой расщепляемой алгебры Ли над полем нулевой характеристики и ее корневого разложения относительно расщепляющей подалгебры Картана.
a+b+g=0, то Nab=Nrg=Nga. Существует нормировка векторов Х а, при которой Nab=-N-a,-b, причем числа Nab получаются рациональными. Существует нормировка векторов Х a, при которой все Nab - целые (см. Шевалле группа). Определение К.- В. б. (введенное Г. Вейлем в [1]), а также все сказанное выше о векторах Х a, h'a. и числах Nab. дословно переносится на случай произвольной конечномерной полупростой расщепляемой алгебры Ли над полем нулевой характеристики и ее корневого разложения относительно расщепляющей подалгебры Картана.
Лит.:[1] Weyl H., "Math. Z.", 1924, Bd 23, S. 271 - 304; [2] Джекобсон Н., Алгебры Ли, пер. с англ., М., 1964; [3] Теория алгебр Ли. Топология групп Ли. пер. с франц., М., 1962.
Д. П. Желобенко.

 где D - система всех ненулевых корней алгебры g относительно т. К.- В. б. выбирается неоднозначно. Корень a(h),
где D - система всех ненулевых корней алгебры g относительно т. К.- В. б. выбирается неоднозначно. Корень a(h), 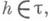 . как линейная форма над т, отождествляется с вектором
. как линейная форма над т, отождествляется с вектором 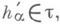 для которого
для которого 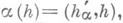
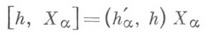
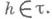 Еслито
Еслито  причем
причем 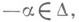 можно выбрать Х a. так, чтобы выполнялось равенство [Х a, X-a] = h'a. Если
можно выбрать Х a. так, чтобы выполнялось равенство [Х a, X-a] = h'a. Если  то
то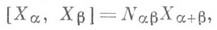
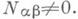 Если а, Р,
Если а, Р, a+b+g=0, то Nab=Nrg=Nga. Существует нормировка векторов Х а, при которой Nab=-N-a,-b, причем числа Nab получаются рациональными. Существует нормировка векторов Х a, при которой все Nab - целые (см. Шевалле группа). Определение К.- В. б. (введенное Г. Вейлем в [1]), а также все сказанное выше о векторах Х a, h'a. и числах Nab. дословно переносится на случай произвольной конечномерной полупростой расщепляемой алгебры Ли над полем нулевой характеристики и ее корневого разложения относительно расщепляющей подалгебры Картана.
a+b+g=0, то Nab=Nrg=Nga. Существует нормировка векторов Х а, при которой Nab=-N-a,-b, причем числа Nab получаются рациональными. Существует нормировка векторов Х a, при которой все Nab - целые (см. Шевалле группа). Определение К.- В. б. (введенное Г. Вейлем в [1]), а также все сказанное выше о векторах Х a, h'a. и числах Nab. дословно переносится на случай произвольной конечномерной полупростой расщепляемой алгебры Ли над полем нулевой характеристики и ее корневого разложения относительно расщепляющей подалгебры Картана.