"
0
C
F
G
H
K
L
N
P
S
T
W
Z
А
Б
В
Г
Д
Е
Ж
З
И
Й
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Ш
Э
Ю
Я
АНАЛИТИЧЕСКОЕ ОТОБРАЖЕНИЕ
Значение АНАЛИТИЧЕСКОЕ ОТОБРАЖЕНИЕ в математической энциклопедии:
аналитический морфизм,- морфизм аналитических пространств, рассматриваемых как окольцованные про странства. А. о. пространства  в пространство
в пространство  есть пара
есть пара  , где
, где

- непрерывное отображение, а

- гомоморфизм пучков колец на X. В случае комплексных пространств А. о. наз. также голоморфным отображением.
В случае, когда  и
и  - приведенные аналитич. ространства, гомоморфизм
- приведенные аналитич. ространства, гомоморфизм  полностью определяется отображением
полностью определяется отображением  п является обратным отображением ростков функций, отвечающим
п является обратным отображением ростков функций, отвечающим  . Таким образом, в этом случае А. о.- это такое отображение
. Таким образом, в этом случае А. о.- это такое отображение  , что для любого
, что для любого  и любого имеет место
и любого имеет место 

Слоем А. о.
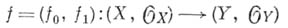
в точке  наз. аналитич. одпространство
наз. аналитич. одпространство

пространства  , где
, где  - пучок ростков функций, обращающихся в 0 в точке у. Если положить
- пучок ростков функций, обращающихся в 0 в точке у. Если положить

то имеет место неравенство

Если  - приведенные комплексные пространства, то для всякого
- приведенные комплексные пространства, то для всякого  множество
множество

является аналитическим в X.
А. о.  наз. плоским в точке
наз. плоским в точке  является плоским модулем над кольцом
является плоским модулем над кольцом  . В этом случае неравенство (*) превращается в равенство. А. о. наз. плоским, если оно - плоское в каждой точке
. В этом случае неравенство (*) превращается в равенство. А. о. наз. плоским, если оно - плоское в каждой точке  . Плоское А. о. комплексных пространств является открытым. Обратно, если
. Плоское А. о. комплексных пространств является открытым. Обратно, если  открыто,
открыто,  гладко, а
гладко, а  и все слои приведены, то
и все слои приведены, то  - плоское А. о. Множество точек комплексного или жесткого аналитич. ространства X, у к-рых А. о.
- плоское А. о. Множество точек комплексного или жесткого аналитич. ространства X, у к-рых А. о.  не является плоским, будет аналитическим в X. Если Xи Y - приведенные комплексные пространства, причем Xимеет счетную базу, то в Yсуществует открытое всюду плотное множество, над к-рым
не является плоским, будет аналитическим в X. Если Xи Y - приведенные комплексные пространства, причем Xимеет счетную базу, то в Yсуществует открытое всюду плотное множество, над к-рым  - плоское А. о. Если А. о.
- плоское А. о. Если А. о.

комплексных пространств плоско, то множества тех  , в к-рых слой
, в к-рых слой  не приведен или ненормален, являются аналитическими в
не приведен или ненормален, являются аналитическими в 
Пусть  - А. о. приведенных комплексных пространств. Если
- А. о. приведенных комплексных пространств. Если  , то существует стратификация
, то существует стратификация

где  - аналитич. множества и
- аналитич. множества и  для больших r , со следующим свойством: всякая точка
для больших r , со следующим свойством: всякая точка  обладает такой окрестностью
обладает такой окрестностью  , что
, что  - локальное аналитич. множество в Y, все неприводимые компоненты ростка к-рого в точке
- локальное аналитич. множество в Y, все неприводимые компоненты ростка к-рого в точке  имеют размерность r. В частности, если
имеют размерность r. В частности, если  собственное, то
собственное, то  - аналитич. множество в X. Этот факт является частным случаем теорем конечности для А. о.
- аналитич. множество в X. Этот факт является частным случаем теорем конечности для А. о.
Пусть  - комплексные пространства, причем Xкомпактно. Тогда множество
- комплексные пространства, причем Xкомпактно. Тогда множество  всех А. о.
всех А. о.  можно снабдить такой структурой комплексного пространства, что отображение
можно снабдить такой структурой комплексного пространства, что отображение

переводящее пару  аналитично.
аналитично.
В частности, группа автоморфизмов компактного комплексного пространства Xявляется комплексной группой Ли, аналитически действующей на X.
Лит.: МRemmert R., "Math. Ann.", 1956, Bd 130, S. 410-41; [2] e г о же, там же, 1957, Bd 133, S. 328-70; ГЗ] Stein К., Analytischer Abbildungen allgemeiner analyti-scher Raume. Colloque de topologie, Strasbourg, Avril, 1954; [4] Frisch J., "Inventiones math.", 1967, Bd 4, S. 118-38.
Д. А. Пономарев.

 в пространство
в пространство  есть пара
есть пара  , где
, где 

 и
и  - приведенные аналитич. ространства, гомоморфизм
- приведенные аналитич. ространства, гомоморфизм  полностью определяется отображением
полностью определяется отображением  п является обратным отображением ростков функций, отвечающим
п является обратным отображением ростков функций, отвечающим  . Таким образом, в этом случае А. о.- это такое отображение
. Таким образом, в этом случае А. о.- это такое отображение  , что для любого
, что для любого  и любого имеет место
и любого имеет место 

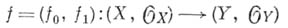
 наз. аналитич. одпространство
наз. аналитич. одпространство 
 , где
, где  - пучок ростков функций, обращающихся в 0 в точке у. Если положить
- пучок ростков функций, обращающихся в 0 в точке у. Если положить 

 - приведенные комплексные пространства, то для всякого
- приведенные комплексные пространства, то для всякого  множество
множество 
 наз. плоским в точке
наз. плоским в точке  является плоским модулем над кольцом
является плоским модулем над кольцом  . В этом случае неравенство (*) превращается в равенство. А. о. наз. плоским, если оно - плоское в каждой точке
. В этом случае неравенство (*) превращается в равенство. А. о. наз. плоским, если оно - плоское в каждой точке  . Плоское А. о. комплексных пространств является открытым. Обратно, если
. Плоское А. о. комплексных пространств является открытым. Обратно, если  открыто,
открыто,  гладко, а
гладко, а  и все слои приведены, то
и все слои приведены, то  - плоское А. о. Множество точек комплексного или жесткого аналитич. ространства X, у к-рых А. о.
- плоское А. о. Множество точек комплексного или жесткого аналитич. ространства X, у к-рых А. о.  не является плоским, будет аналитическим в X. Если Xи Y - приведенные комплексные пространства, причем Xимеет счетную базу, то в Yсуществует открытое всюду плотное множество, над к-рым
не является плоским, будет аналитическим в X. Если Xи Y - приведенные комплексные пространства, причем Xимеет счетную базу, то в Yсуществует открытое всюду плотное множество, над к-рым  - плоское А. о. Если А. о.
- плоское А. о. Если А. о.
 , в к-рых слой
, в к-рых слой  не приведен или ненормален, являются аналитическими в
не приведен или ненормален, являются аналитическими в 
 - А. о. приведенных комплексных пространств. Если
- А. о. приведенных комплексных пространств. Если  , то существует стратификация
, то существует стратификация
 - аналитич. множества и
- аналитич. множества и  для больших r , со следующим свойством: всякая точка
для больших r , со следующим свойством: всякая точка  обладает такой окрестностью
обладает такой окрестностью  , что
, что  - локальное аналитич. множество в Y, все неприводимые компоненты ростка к-рого в точке
- локальное аналитич. множество в Y, все неприводимые компоненты ростка к-рого в точке  имеют размерность r. В частности, если
имеют размерность r. В частности, если  собственное, то
собственное, то  - аналитич. множество в X. Этот факт является частным случаем теорем конечности для А. о.
- аналитич. множество в X. Этот факт является частным случаем теорем конечности для А. о. - комплексные пространства, причем Xкомпактно. Тогда множество
- комплексные пространства, причем Xкомпактно. Тогда множество  всех А. о.
всех А. о.  можно снабдить такой структурой комплексного пространства, что отображение
можно снабдить такой структурой комплексного пространства, что отображение 
 аналитично.
аналитично.