Математический словарь
|
"
0
C
F
G
H
K
L
N
P
S
T
W
Z
А
Б
В
Г
Д
Е
Ж
З
И
Й
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Ш
Э
Ю
Я
КАРЛСОНА НЕРАВЕНСТВОЗначение КАРЛСОНА НЕРАВЕНСТВО в математической энциклопедии: пусть {а п,1<n<
Установлено Ф. Карлсоном [1]. Интегральный аналог К. н.: если f(x)>0,
Константа p2 является наилучшей в том смысле, что существует последовательность а п такая, для к-рой правая часть (1) сколь угодно близка к левой, и существует функция f(x)такая, для к-рой знак равенства в (2) достигается. Лит.:[1] Carlson P., "Ark. mat., astron. och fys.", 1934, Bd 25A, №7, S. 1 - 13; [2] Xapди Г. Г., Литтльвуд Д ж. Е., Полна Г., Неравенства, пер. с англ., М., 1948. М. И. Войцеховский. |
|
|
|

 } - не все равные нулю неотрицательные действительные числа, тогда:
} - не все равные нулю неотрицательные действительные числа, тогда: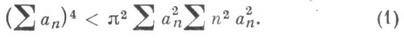
 , f,
, f, 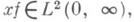 то
то