|
"
0
C
F
G
H
K
L
N
P
S
T
W
Z
А
Б
В
Г
Д
Е
Ж
З
И
Й
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Ш
Э
Ю
Я
КАРАТЕОДОРИ ТЕОРЕМАЗначение КАРАТЕОДОРИ ТЕОРЕМА в математической энциклопедии: о конформном отображении областей с переменными границами - один из основных результатов теории конформных отображений областей с переменными границами; получен К. Каратеодори [1]. Пусть дана последовательность односвязных областей В п, п=1,2, . . ., плоскости z, содержащих фиксированную точку z0, Теорема Каратеодори. Пусть дана последовательность функций z=fn(x), fn(x0)=z0, f'n(x0)>0, n=1,2,..., регулярных и однолистных в круге |z-z0| <1 и отображающих |z-z0| <1 соответственно на области В п. Для того чтобы функций fn(z), n=1, 2,..., сходились в круге |x-x0| <1 к конечной функции f(x), необходимо и достаточно, чтобы последовательность областей В п, n=1, 2,..., сходилась к ядру В, к-рое есть либо точка z0, либо область, имеющая более одной граничной точки. При этом сходимость равномерна внутри круга |x-x0|<1. Если предельная функция Аналогично рассматривается вопрос о сходимости последовательности функций, однолистных в многосвязных областях. Ниже приводится одна из таких теорем для неограниченных областей. Пусть дана последовательность любых областей В п, n=1, 2,..., плоскости z, содержащих нек-рую фиксированную окрестность точки В п, n=1, 2,..., относительно точки Можно указать и другие теоремы о сходимости последовательностей однолистных функций в зависимости от способа их нормировки (см. [2]). Лит.:[1] Caratheodory С, "Math. Ann.", 1912, Bd 72, S. 107-44; [2] Голузин Г. М., Геометрическая теория функций комплексного переменного, 2 изд., М., 1966. Г. В. Кузьмина. |
|
|
|

 Если существует круг |z-z0|<r, r>0, принадлежащий всем областям В п, то ядром последовательности В п, n = 1, 2, ..., относительно точки z0 наз. наибольшая область В, содержащая точку z0 и обладающая тем свойством, что для всякого компакта Е, принадлежащего В, существует такое число N, что Епринадлежит областям В п при
Если существует круг |z-z0|<r, r>0, принадлежащий всем областям В п, то ядром последовательности В п, n = 1, 2, ..., относительно точки z0 наз. наибольшая область В, содержащая точку z0 и обладающая тем свойством, что для всякого компакта Е, принадлежащего В, существует такое число N, что Епринадлежит областям В п при  Наибольшая область понимается в том смысле, что она содержит любую другую область, обладающую тем же свойством. Если указанного круга не существует, то под ядром Впоследовательности В n, п= 1, 2, . . ., понимается точка z0 (в этом случае говорят, что последовательность областей В п, n=1, 2, ..., имеет вырожденное ядро). Последовательность областей В п, n=1, 2,..., сходится к ядру В, если любая последовательность из В п имеет своим ядром также В.
Наибольшая область понимается в том смысле, что она содержит любую другую область, обладающую тем же свойством. Если указанного круга не существует, то под ядром Впоследовательности В n, п= 1, 2, . . ., понимается точка z0 (в этом случае говорят, что последовательность областей В п, n=1, 2, ..., имеет вырожденное ядро). Последовательность областей В п, n=1, 2,..., сходится к ядру В, если любая последовательность из В п имеет своим ядром также В.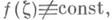 то она однолистно отображает круг |x-x0| <1 на ядро В, а обратные функции jn(z), n=1,2,. .., равномерно сходятся внутри Вк функции j(z), обратной к f(x).
то она однолистно отображает круг |x-x0| <1 на ядро В, а обратные функции jn(z), n=1,2,. .., равномерно сходятся внутри Вк функции j(z), обратной к f(x). Ядром последовательности
Ядром последовательности наз. наибольшая область В, содержащая
наз. наибольшая область В, содержащая  любая замкнутая подобласть к-рой принадлежит всем В п, начиная с некоторого п. Сходимость последовательности областей В п, п=1,2,..., к ядру Вопределяется, как и выше. Имеет место следующая теорема [2]. Пусть в плоскости z дана последовательность областей А п, n=1, 2,..., содержащих
любая замкнутая подобласть к-рой принадлежит всем В п, начиная с некоторого п. Сходимость последовательности областей В п, п=1,2,..., к ядру Вопределяется, как и выше. Имеет место следующая теорема [2]. Пусть в плоскости z дана последовательность областей А п, n=1, 2,..., содержащих  и сходящихся к ядру А, и пусть функции x=fn(z), n=1, 2,..., однолистно отображают их соответственно на области В п, бодержащие
и сходящихся к ядру А, и пусть функции x=fn(z), n=1, 2,..., однолистно отображают их соответственно на области В п, бодержащие 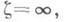
 n=1, 2,. .. Для того чтобы функции fn(z), n=1, 2,..., равномерно сходились внутри области Ак однолистной функции f(z), необходимо и достаточно, чтобы последовательность областей В п, n=1, 2,. .., имела ядро Ви сходилась к нему, причем тогда функция x=f(z) однолистно отображает Ана В.
n=1, 2,. .. Для того чтобы функции fn(z), n=1, 2,..., равномерно сходились внутри области Ак однолистной функции f(z), необходимо и достаточно, чтобы последовательность областей В п, n=1, 2,. .., имела ядро Ви сходилась к нему, причем тогда функция x=f(z) однолистно отображает Ана В.