|
"
0
C
F
G
H
K
L
N
P
S
T
W
Z
А
Б
В
Г
Д
Е
Ж
З
И
Й
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Ш
Э
Ю
Я
КАРАТЕОДОРИ МЕРАЗначение КАРАТЕОДОРИ МЕРА в математической энциклопедии: - мера m, порожденная внешней мерой Каратеодори m*, где внешняя мера Каратеодори есть внешняя мера, определенная на классе всех подмножеств метрич. пространства М(с метрикой р) и такая, что
если р( А, B)>0. Введена К. Каратеодори [1]. Множество
для любого Лит.:[1] Caratheodory С, "Nachr. Ges. Wiss. Gottingen", 1914, 404-26; [2] Сакс С, Теория интеграла, пер. с англ., М., 1949; [3] Xалмош П., Теория меры, пер. С англ., М., 1953. В. В. Сазонов. |
|
|
|
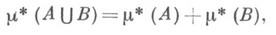
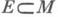принадлежит области определения р., т. е. m*-измеримо, тогда и только тогда, когда
(здесь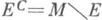 
); если Еm*-измеримо, то m(E) =m*(E). Область определения К. м. содержит все борелевские множества. Если m* - внешняя мера в классе всех подмножеств метрич. пространства такая, что всякое открытое множество m*-измеримо, то m* - внешняя К. м.