"
0
C
F
G
H
K
L
N
P
S
T
W
Z
А
Б
В
Г
Д
Е
Ж
З
И
Й
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Ш
Э
Ю
Я
АБЕЛЕВ ДИФФЕРЕНЦИАЛ
Значение АБЕЛЕВ ДИФФЕРЕНЦИАЛ в математической энциклопедии:
голоморфный или мероморфный дифференциал на компактной, или замкнутой, римановой поверхности S(см. Дифференциал на римановой поверхности).
Пусть g - род поверхности S; а1b1 а 2b2...agbg циклы канонич. базиса гомологии S. В зависимости от характера особенностей различают А. д. трех родов: I, II и III, причем имеют место строгие включения:  А. <д. I рода- это голоморфные всюду на Sдифференциалы 1-го порядка, к-рые в окрестности U ' каждой точки
А. <д. I рода- это голоморфные всюду на Sдифференциалы 1-го порядка, к-рые в окрестности U ' каждой точки  имеют вид
имеют вид  где
где  - локальная униформизирующая переменная в U,
- локальная униформизирующая переменная в U, - голоморфная, или регулярная, аналитич. функция от z в U. Сложение А. д. и умножение на голоморфную функцию определяются естественными правилами: если
- голоморфная, или регулярная, аналитич. функция от z в U. Сложение А. д. и умножение на голоморфную функцию определяются естественными правилами: если

то

А. д. I рода образуют векторное пространство  размерности g. После введения скалярного произведения
размерности g. После введения скалярного произведения

где  - внешнее произведениеw на звездно сопряженный дифференциал
- внешнее произведениеw на звездно сопряженный дифференциал 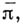 пространство
пространство 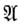 превращается в гильбертово пространство.
превращается в гильбертово пространство.
Пусть  суть А- и B-периоды А. д. 1 рода
суть А- и B-периоды А. д. 1 рода  , т. е. интегралы
, т. е. интегралы

Тогда имеет место соотношение:

Если А'1 ,B'1 ,А'2 ,B'2 ,...,А'g ,B'g , - периоды другого А. д. I рода p, то

Соотношения (1) и (2) наз. билинейными соотношениями Римана для А. д. I рода. Канонич. базис А. д. I рода, т. е. канонич. базис j1  пространства
пространства  выбирается таким образом, что
выбирается таким образом, что

где  и
и  при
при  При этом матрица (Bi j) i, j=1,2,...,gn B-периодов
При этом матрица (Bi j) i, j=1,2,...,gn B-периодов 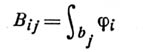 симметрическая, а матрица мнимых частей
симметрическая, а матрица мнимых частей 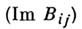 положительно определенная. А. д. I рода, у к-рого все A-периоды или все B-периоды равны нулю, тождественно равен нулю. Если все периоды А. д. I рода
положительно определенная. А. д. I рода, у к-рого все A-периоды или все B-периоды равны нулю, тождественно равен нулю. Если все периоды А. д. I рода  действительны, то
действительны, то 
А. д. II и III рода относятся, вообще говоря, к мероморфным дифференциалам, т. е. к таким аналитич. дифференциалам, к-рые имеют на Sне более чем конечное множество особенностей типа полюсов с локальным представлением

где  - регулярная функция, п - порядок полюса (если
- регулярная функция, п - порядок полюса (если  ),
),  - вычет в данном полюсе. При
- вычет в данном полюсе. При 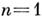 полюс наз. простым. А. д. II рода - это мероморфные дифференциалы, у к-рых все вычеты равны нулю, т. е. мероморфные дифференциалы с локальным представлением
полюс наз. простым. А. д. II рода - это мероморфные дифференциалы, у к-рых все вычеты равны нулю, т. е. мероморфные дифференциалы с локальным представлением

А. д. III рода - это А. д. произвольного вида.
Если  - произвольный А. д. с A-периодами А 1 , А 2 ,.. ., Ag, то А. д.
- произвольный А. д. с A-периодами А 1 , А 2 ,.. ., Ag, то А. д. имеет нулевые А-периоды и наз. нормированным А. д. В частности, если
имеет нулевые А-периоды и наз. нормированным А. д. В частности, если 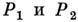 - любые различные точки S, то можно построить нормированный А. д.
- любые различные точки S, то можно построить нормированный А. д.  с особенностями
с особенностями  в
в  к-рый наз. нормальным А. д. III рода. Пусть
к-рый наз. нормальным А. д. III рода. Пусть  - произвольный А. д. с вычетами
- произвольный А. д. с вычетами  в точках
в точках 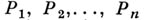 соответственно, при этом всегда
соответственно, при этом всегда  Если Р 0 - произвольная точка на Sтакая, что
Если Р 0 - произвольная точка на Sтакая, что  можно представить в виде линейной комбинации нормированного А. д. II рода
можно представить в виде линейной комбинации нормированного А. д. II рода  конечного числа нормальных А. д. III рода
конечного числа нормальных А. д. III рода  и базисных А. д. I рода
и базисных А. д. I рода 
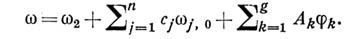
Пусть  - А. д. III рода, имеющий только простые полюсы с вычетами в точках - произвольный А. д.
- А. д. III рода, имеющий только простые полюсы с вычетами в точках - произвольный А. д. I рода;
I рода;

причем циклы  не проходят через полюсы
не проходят через полюсы  Пусть точка
Пусть точка  не лежит на циклах
не лежит на циклах  есть путь от P0 к Pj. Тогда имеем билинейные соотношения для А. д. I и III рода:
есть путь от P0 к Pj. Тогда имеем билинейные соотношения для А. д. I и III рода:
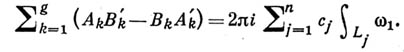
Между А. д. I и II рода также имеются билинейные соотношения аналогичного вида.
Произвольный А. д. III рода, кроме А- и 5-перио-дов  наз. циклическими периодами, имеет еще полярные периоды вида
наз. циклическими периодами, имеет еще полярные периоды вида  вдоль циклов, гомологичных нулю, но охватывающих полюсы
вдоль циклов, гомологичных нулю, но охватывающих полюсы  Таким образом, для произвольного цикла
Таким образом, для произвольного цикла  имеем:
имеем:

где  - целые числа.
- целые числа.
Важные свойства А. д. описываются в терминах дивизоров. Пусть  - дивизор А. д.
- дивизор А. д. 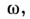 т. е. выражение вида
т. е. выражение вида  где
где  - все нули и полюсы
- все нули и полюсы  - их кратности, или порядки. Степень дивизора
- их кратности, или порядки. Степень дивизора  для А. д.
для А. д.  зависит только от рода S, а именно всегда
зависит только от рода S, а именно всегда  Пусть
Пусть  - нек-рый произвольно заданный дивизор. Обозначим через
- нек-рый произвольно заданный дивизор. Обозначим через 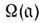 комплексное векторное пространство А. д.
комплексное векторное пространство А. д.  дивизоры к-рых
дивизоры к-рых  кратны а;
кратны а;  - векторное пространство мероморфных функций f на S, дивизоры к-рых
- векторное пространство мероморфных функций f на S, дивизоры к-рых  кратны
кратны  Тогда размерность
Тогда размерность  . Другая важная информация о размерности этих пространств содержится в теореме Римана- Роха: для любого дивизора
. Другая важная информация о размерности этих пространств содержится в теореме Римана- Роха: для любого дивизора  имеем равенство:
имеем равенство:
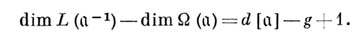
Отсюда следует, напр., что при  т. е. на поверхности тора, мероморфная функция не может иметь единственный простой полюс.
т. е. на поверхности тора, мероморфная функция не может иметь единственный простой полюс.
Пусть S - произвольная компактная риманова поверхность, на к-рой z и w - мероморфные функции, удовлетворяющие неприводимому алгебраич. уравнению  Произвольный А. д.
Произвольный А. д.  на S можно выразить тогда в виде
на S можно выразить тогда в виде  где
где  - нек-рая рациональная функция от
- нек-рая рациональная функция от  и
и  , и обратно: выражение
, и обратно: выражение  есть А. д. Таким образом, произвольный абелев интеграл
есть А. д. Таким образом, произвольный абелев интеграл

является интегралом от нек-рого А. д. на компактной римановой поверхности S.
См. также Алгебраическая функция.
Лит.:[1]Спрингер Дж., Введение в теорию римановых поверхностей, пер. с англ., М., 1960; [2] Неванлинна Р., Униформизация, пер. с нем., М., 1955; [3] Чеботарев Н. Г., Теория алгебраических функций, М.- Л., 1948.
Е. Д. Соломенцев.

 А. <д. I рода- это голоморфные всюду на Sдифференциалы 1-го порядка, к-рые в окрестности U ' каждой точки
А. <д. I рода- это голоморфные всюду на Sдифференциалы 1-го порядка, к-рые в окрестности U ' каждой точки  имеют вид
имеют вид  где
где  - локальная униформизирующая переменная в U,
- локальная униформизирующая переменная в U, - голоморфная, или регулярная, аналитич. функция от z в U. Сложение А. д. и умножение на голоморфную функцию определяются естественными правилами: если
- голоморфная, или регулярная, аналитич. функция от z в U. Сложение А. д. и умножение на голоморфную функцию определяются естественными правилами: если 

 размерности g. После введения скалярного произведения
размерности g. После введения скалярного произведения 
 - внешнее произведениеw на звездно сопряженный дифференциал
- внешнее произведениеw на звездно сопряженный дифференциал 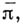 пространство
пространство 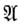 превращается в гильбертово пространство.
превращается в гильбертово пространство. суть А- и B-периоды А. д. 1 рода
суть А- и B-периоды А. д. 1 рода  , т. е. интегралы
, т. е. интегралы 


 пространства
пространства  выбирается таким образом, что
выбирается таким образом, что
 и
и  при
при  При этом матрица (Bi j) i, j=1,2,...,gn B-периодов
При этом матрица (Bi j) i, j=1,2,...,gn B-периодов 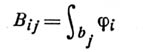 симметрическая, а матрица мнимых частей
симметрическая, а матрица мнимых частей 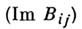 положительно определенная. А. д. I рода, у к-рого все A-периоды или все B-периоды равны нулю, тождественно равен нулю. Если все периоды А. д. I рода
положительно определенная. А. д. I рода, у к-рого все A-периоды или все B-периоды равны нулю, тождественно равен нулю. Если все периоды А. д. I рода  действительны, то
действительны, то 

 - регулярная функция, п - порядок полюса (если
- регулярная функция, п - порядок полюса (если  ),
),  - вычет в данном полюсе. При
- вычет в данном полюсе. При 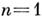 полюс наз. простым. А. д. II рода - это мероморфные дифференциалы, у к-рых все вычеты равны нулю, т. е. мероморфные дифференциалы с локальным представлением
полюс наз. простым. А. д. II рода - это мероморфные дифференциалы, у к-рых все вычеты равны нулю, т. е. мероморфные дифференциалы с локальным представлением 
 - произвольный А. д. с A-периодами А 1 , А 2 ,.. ., Ag, то А. д.
- произвольный А. д. с A-периодами А 1 , А 2 ,.. ., Ag, то А. д. имеет нулевые А-периоды и наз. нормированным А. д. В частности, если
имеет нулевые А-периоды и наз. нормированным А. д. В частности, если 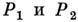 - любые различные точки S, то можно построить нормированный А. д.
- любые различные точки S, то можно построить нормированный А. д.  с особенностями
с особенностями  в
в  к-рый наз. нормальным А. д. III рода. Пусть
к-рый наз. нормальным А. д. III рода. Пусть  - произвольный А. д. с вычетами
- произвольный А. д. с вычетами  в точках
в точках 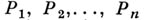 соответственно, при этом всегда
соответственно, при этом всегда  Если Р 0 - произвольная точка на Sтакая, что
Если Р 0 - произвольная точка на Sтакая, что  можно представить в виде линейной комбинации нормированного А. д. II рода
можно представить в виде линейной комбинации нормированного А. д. II рода  конечного числа нормальных А. д. III рода
конечного числа нормальных А. д. III рода  и базисных А. д. I рода
и базисных А. д. I рода 
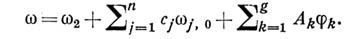
 - А. д. III рода, имеющий только простые полюсы с вычетами в точках - произвольный А. д.
- А. д. III рода, имеющий только простые полюсы с вычетами в точках - произвольный А. д. I рода;
I рода;

 не проходят через полюсы
не проходят через полюсы  Пусть точка
Пусть точка  не лежит на циклах
не лежит на циклах  есть путь от P0 к Pj. Тогда имеем билинейные соотношения для А. д. I и III рода:
есть путь от P0 к Pj. Тогда имеем билинейные соотношения для А. д. I и III рода: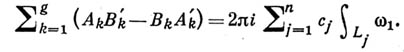
 наз. циклическими периодами, имеет еще полярные периоды вида
наз. циклическими периодами, имеет еще полярные периоды вида  вдоль циклов, гомологичных нулю, но охватывающих полюсы
вдоль циклов, гомологичных нулю, но охватывающих полюсы  Таким образом, для произвольного цикла
Таким образом, для произвольного цикла  имеем:
имеем:
 - целые числа.
- целые числа. - дивизор А. д.
- дивизор А. д. 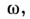 т. е. выражение вида
т. е. выражение вида  где
где  - все нули и полюсы
- все нули и полюсы  - их кратности, или порядки. Степень дивизора
- их кратности, или порядки. Степень дивизора  для А. д.
для А. д.  зависит только от рода S, а именно всегда
зависит только от рода S, а именно всегда  Пусть
Пусть  - нек-рый произвольно заданный дивизор. Обозначим через
- нек-рый произвольно заданный дивизор. Обозначим через 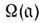 комплексное векторное пространство А. д.
комплексное векторное пространство А. д.  дивизоры к-рых
дивизоры к-рых  кратны а;
кратны а;  - векторное пространство мероморфных функций f на S, дивизоры к-рых
- векторное пространство мероморфных функций f на S, дивизоры к-рых  кратны
кратны  Тогда размерность
Тогда размерность  . Другая важная информация о размерности этих пространств содержится в теореме Римана- Роха: для любого дивизора
. Другая важная информация о размерности этих пространств содержится в теореме Римана- Роха: для любого дивизора  имеем равенство:
имеем равенство: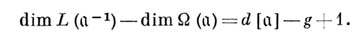
 т. е. на поверхности тора, мероморфная функция не может иметь единственный простой полюс.
т. е. на поверхности тора, мероморфная функция не может иметь единственный простой полюс. Произвольный А. д.
Произвольный А. д.  на S можно выразить тогда в виде
на S можно выразить тогда в виде  где
где  - нек-рая рациональная функция от
- нек-рая рациональная функция от  и
и  , и обратно: выражение
, и обратно: выражение  есть А. д. Таким образом, произвольный абелев интеграл
есть А. д. Таким образом, произвольный абелев интеграл