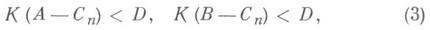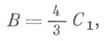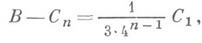|
"
0
C
F
G
H
K
L
N
P
S
T
W
Z
А
Б
В
Г
Д
Е
Ж
З
И
Й
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Ш
Э
Ю
Я
ИСЧЕРПЫВАНИЯ МЕТОДЗначение ИСЧЕРПЫВАНИЯ МЕТОД в математической энциклопедии: - метод доказательства, применявшийся математиками древности при нахождении площадей и объемов. Назв. "метод исчерпывания" введено в 17 в. Типичная схема доказательства при помощи И. м. может быть изложена в современных обозначениях так: для определения величины Астроится нек-рая последовательность величин C1, C2, ..., С п,... так, что
предполагают также известным такое В, что
и при любом целом Кдля достаточно больших пудовлетворяются неравенства
где D- постоянно. С современной точки зрения, для перехода от неравенства (3) к равенству
достаточно заметить, что из условий (1), (2) и (3) следует
Математики древности, не располагавшие теорией пределов, обращались к доказательству от противного и доказывали невозможность каждого из неравенств А<В, В<А. Чтобы опровергнуть первое из них, при помощи Архимеда аксиомы устанавливали, что для R=B-A существует такое К, что KR>D, и в силу условия (1) получали
что противоречит второму из неравенств (3). Аналогично опровергалось другое предположение. После этого оставалось принять только равенство (4). Введение И. м. вместе с лежащей в его основе аксиомой приписывается Евдоксу Книдскому. Этим методом широко пользовался Евклид, а с особенным искусством и разнообразием - Архимед. Напр., для определения площади сегмента Апараболы Архимед строит площади С 1, С 2,.. .,"исчерпывающие" при их постепенном нарастании площадь Асегмента. При этом
Вместо того чтобы прибегнуть к предельному переходу
Архимед геометрически доказывает, что при любом п
Вводя площадь
Архимед получает, что
и, следуя изложенному выше порядку, закапчивает доказательство того, что
|
|
|
|