"
0
C
F
G
H
K
L
N
P
S
T
W
Z
А
Б
В
Г
Д
Е
Ж
З
И
Й
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Ш
Э
Ю
Я
АНАЛИТИЧЕСКИЙ ПОЛИЭДРЗначение АНАЛИТИЧЕСКИЙ ПОЛИЭДР в математической энциклопедии:
область П комплексного пространства 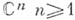 , представпмая посредством неравенств , представпмая посредством неравенств 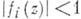 , где функция , где функция  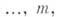 голоморфны в нек-рой области голоморфны в нек-рой области 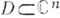 , содержащей , содержащей  , то есть , то есть 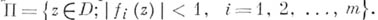
Предполагается также, что 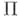 компактна в D. В случае, еслп компактна в D. В случае, еслп 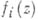 - полиномы, А. п. наз. полиномиальным полиэдром. Если - полиномы, А. п. наз. полиномиальным полиэдром. Если  и и  А. п. является поликругом. Гранями А. п. наз. множества А. п. является поликругом. Гранями А. п. наз. множества 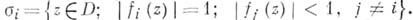
Пересечение любых kразличных граней 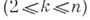 наз. ребром А. п. Если наз. ребром А. п. Если 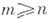 и все грани имеют размерность и все грани имеют размерность 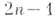 , а каждое ребро - размерность не выше , а каждое ребро - размерность не выше  , то А. п. есть Вейля область. Совокупность n-мерных ребер , то А. п. есть Вейля область. Совокупность n-мерных ребер 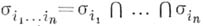 образует остов А. п. Понятие А. п. играет существенную роль в вопросах интегральных представлений аналитич. функций многих переменных. образует остов А. п. Понятие А. п. играет существенную роль в вопросах интегральных представлений аналитич. функций многих переменных.
Лит.:[I] Шабат Б. В., Введение в комплексный анализ, 2 изд., ч. 2, М., 1976. Е. Д. Соломенцев.
|

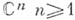 , представпмая посредством неравенств
, представпмая посредством неравенств 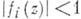 , где функция
, где функция 
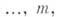 голоморфны в нек-рой области
голоморфны в нек-рой области 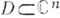 , содержащей
, содержащей  , то есть
, то есть 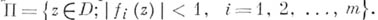
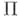 компактна в D. В случае, еслп
компактна в D. В случае, еслп 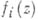 - полиномы, А. п. наз. полиномиальным полиэдром. Если
- полиномы, А. п. наз. полиномиальным полиэдром. Если  и
и  А. п. является поликругом. Гранями А. п. наз. множества
А. п. является поликругом. Гранями А. п. наз. множества 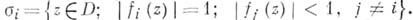
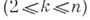 наз. ребром А. п. Если
наз. ребром А. п. Если 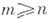 и все грани имеют размерность
и все грани имеют размерность 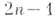 , а каждое ребро - размерность не выше
, а каждое ребро - размерность не выше  , то А. п. есть Вейля область. Совокупность n-мерных ребер
, то А. п. есть Вейля область. Совокупность n-мерных ребер 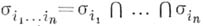 образует остов А. п. Понятие А. п. играет существенную роль в вопросах интегральных представлений аналитич. функций многих переменных.
образует остов А. п. Понятие А. п. играет существенную роль в вопросах интегральных представлений аналитич. функций многих переменных.