Математический словарь
|
"
0
C
F
G
H
K
L
N
P
S
T
W
Z
А
Б
В
Г
Д
Е
Ж
З
И
Й
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Ш
Э
Ю
Я
ИРРАЦИОНАЛЬНОСТИ МЕРАЗначение ИРРАЦИОНАЛЬНОСТИ МЕРА в математической энциклопедии: действительного числа x - функция
где минимум берется по всевозможным парам h0, h1 целых рациональных чисел таких, что
Понятие И. м. является частным случаем понятий линейной независимости меры и трансцендентности меры. И. м. показывает, насколько "хорошо" может число x быть приближено рациональными дробями. Для всех действительных иррациональных чисел x выполняется неравенство
но при любом e>0 для почти всех (в смысле меры Лебега) действительных x
где С=С(e, x)>0. Однако для любой функции j(H)->0 при Лит.:[1] Xинчин А. Я., Цепные дроби, 3 изд., М. 1978. А. И. Галочкин. |
|
|
|

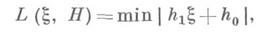
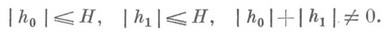

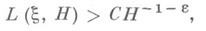
 и j(H)>0 существует число
и j(H)>0 существует число  такое, что при всех
такое, что при всех