|
"
0
C
F
G
H
K
L
N
P
S
T
W
Z
А
Б
В
Г
Д
Е
Ж
З
И
Й
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Ш
Э
Ю
Я
ИНЪЕКТИВНЫЙ МОДУЛЬЗначение ИНЪЕКТИВНЫЙ МОДУЛЬ в математической энциклопедии: - инъективный объект в категории модулей над кольцом R, т. е. такой R-модуль Енад ассоциативным кольцом R с единицей, что для любых R-модулей М, N, для любого мономорфизма i:
точна; 2) любая точная последовательность R-модулей, имеющая вид
расщепляется, т. е. подмодуль Im a=Кеr (5 выделяется в Мпрямым слагаемом; 3) В категории R-модулей "достаточно много" инъективных объектов: каждый R-модуль Мможно вложить в И. м. Более того, каждый модуль Мсодержится в своей инъективной оболочке Е(М), то есть в И. м. Е(М), каждый ненулевой подмодуль к-рого имеет ненулевое пересечение с М. Любое вложение модуля Мв И. м. Епродолжается до вложения инъективной оболочки Е(М)в Е. Каждый R-модуль Мобладает инъективной резольвентой
т. е. точной последовательностью модулей, в к-рой все модули Ei, Прямое произведение И. м. есть И. м. Инъективный модуль Еравен Е r для любого элемента И. м. широко используются при описании различных классов колец (см. Гомологическая классификация колец). Так, все модули над кольцом инъективны тогда и только тогда, когда кольцо классически полупросто. Равносильны условия: R - нётерово справа кольцо; любая прямая сумма инъективных R-модулей инъективна; любой инъективный R-модуль разлагается в прямую сумму неразложимых R-модулей. Артиновость справа кольца R равносильна тому, что каждый И. м. является прямой суммой инъективных оболочек простых модулей. Наследственность справа кольца равносильна инъективности всех фактормодулей инъективных R-модулей, а также тому, что сумма двух инъективных подмодулей в произвольном R-модуле инъективна. Если кольцо R наследственно справа и нётерово справа, то каждый R-модуль содержит наибольший инъективный подмодуль. Проективность (инъективность) всех инъективных (проективных) R-модулей эквивалентна тому, что R является квазифробениусовым кольцом. Инъективная оболочка модуля RR играет важную роль в теории колец частных. Напр., если правый сингулярный идеал кольца Л равен нулю, Е- инъективная оболочка модуля RR, В связи с различными задачами продолжения гомоморфизмов модулей рассматриваются классы модулей М, близких к инъективным: квазиинъективные (если Лит.:[1] Картан А., Эйленберг С, Гомологическая алгебра, пер. с англ., М., 1960; [2] Маклейн С, Гомология, пер. с англ., М., 1966; [3] Faith С, Lectures on injective modules and quotient rings, B.-Hdlb.-N.Y., 1967; [4] Sharpe D. W., Vamos P., Injective modules, Camb., 1972. А. В. Михалев, А. А. Туганбаев. |
|
|
|

 и для любого гомоморфизма f:
и для любого гомоморфизма f: найдется такой гомоморфизм g:
найдется такой гомоморфизм g: что диаграмма коммутативна (все R-модули предполагаются правыми). Следующие условия на R-модуль Еравносильны его инъективности: 1) для любой точной последовательности
что диаграмма коммутативна (все R-модули предполагаются правыми). Следующие условия на R-модуль Еравносильны его инъективности: 1) для любой точной последовательности индуцированная последовательность
индуцированная последовательность


 для всех R-модулей С; 4) для сякого правого идеала I кольца R любой гомоморфизм R-модулей f:
для всех R-модулей С; 4) для сякого правого идеала I кольца R любой гомоморфизм R-модулей f: может быть продолжен до гомоморфизма R-модулей g:
может быть продолжен до гомоморфизма R-модулей g: (критерий Бэра).
(критерий Бэра).
 . инъективны. Длина самой короткой инъективной резольвенты наз. инъективной размерностью модуля (см. также Гомологическая размерность).
. инъективны. Длина самой короткой инъективной резольвенты наз. инъективной размерностью модуля (см. также Гомологическая размерность). не являющегося левым делителем нуля в R, т. е. И. м.- делимый модуль. В частности, абелева группа является И. <м. над кольцом Zтогда и только тогда, когда она делимая. Над коммутативным нётеровым кольцом R каждый И. м.- прямая сумма инъективных оболочек модулей вида R/P, где Р- простой идеал кольца R.
не являющегося левым делителем нуля в R, т. е. И. м.- делимый модуль. В частности, абелева группа является И. <м. над кольцом Zтогда и только тогда, когда она делимая. Над коммутативным нётеровым кольцом R каждый И. м.- прямая сумма инъективных оболочек модулей вида R/P, где Р- простой идеал кольца R. - ее кольцо эндоморфизмов, то R-модули
- ее кольцо эндоморфизмов, то R-модули  и ER изоморфны, Еявляется кольцом, изоморфным кольцу L, и это кольцо оказывается максимальным правым кольцом частных кольца R, причем
и ER изоморфны, Еявляется кольцом, изоморфным кольцу L, и это кольцо оказывается максимальным правым кольцом частных кольца R, причем  - самоинъективное справа регулярное (в смысле Неймана) кольцо.
- самоинъективное справа регулярное (в смысле Неймана) кольцо. и f :
и f : то f продолжается до эндоморфизма модуля М);псевдоинъективные (если
то f продолжается до эндоморфизма модуля М);псевдоинъективные (если  f:
f: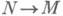 и f - мономорфизм, то f продолжается до эндоморфизма модуля М);малоинъективные (все эндоморфизмы подмодулей продолжаются до эндоморфизмов модуля М). Квазиинъективность модуля Мравносильна инвариантности модуля Мв своей инъективной оболочке относительно ее эндоморфизмов.
и f - мономорфизм, то f продолжается до эндоморфизма модуля М);малоинъективные (все эндоморфизмы подмодулей продолжаются до эндоморфизмов модуля М). Квазиинъективность модуля Мравносильна инвариантности модуля Мв своей инъективной оболочке относительно ее эндоморфизмов.