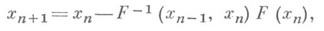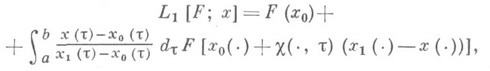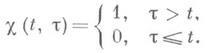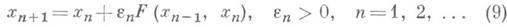|
"
0
C
F
G
H
K
L
N
P
S
T
W
Z
А
Б
В
Г
Д
Е
Ж
З
И
Й
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Ш
Э
Ю
Я
ИНТЕРПОЛИРОВАНИЕЗначение ИНТЕРПОЛИРОВАНИЕ в математической энциклопедии: в вычислительной математике - способ приближенного или точного нахождения какой-либо величины по известным отдельным значениям этой же или других величин, связанных с ней. На основе И. построен ряд приближенных методов решения математич. задач. Наибольшее значение в вычислительной математике имеет задача построения способов интерполирования функций. Интерполяция функционалов и операторов также широко используется при построении приближенных методов. Приближенное представление и вычисление функций. И. функций рассматривается как один из способов их приближения. И. функции f(x)на отрезке [ а, b]по значениям ее в узлах xk сетки Обычно Ln(x)строится в виде
где {ji(x)}- некоторая заранее выбранная система линейно независимых функций. Такое И. наз. линейным относительно системы {ji(x)}, a Ln(x)- интерполяционным полиномом по системе Выбор системы {ji(x)}определяется свойством того класса функций, для приближения к-рых предназначаются интерполяционные формулы. Напр., для приближения 2p-периодических функций на [0, 2p] за {ji(x)}естественно взять тригонометрическую систему функций, для приближения на полуоси [0, беск.) ограниченных или возрастающих функций - систему рациональных или показательных функций, учитывающих поведение приближаемых функций на бесконечности и т. Д. Чаще всего используется алгебраич. И.: ji(x)=х i, простейший вариант которого - линейное интерполирование с двумя узлами И. xk и xk+1- определяется формулой
Алгебраическое И. более высокого порядка в задаче приближения функций на всем отрезке [ а, b]применяется на практике сравнительно редко. Обычно ограничиваются линейным И. по формуле (1) или квадратичным интерполированием с тремя узлами на частичных отрезках сетки по формуле
Имеются различные варианты записи алгебраич. интерполяционных многочленов (см. Интерполяционная формула). Находит все большее применение И. сплайнами (см. Интерполяционный сплайн). На практике чаще всего используются параболические или кубические сплайны. Интерполяционным кубическим сплайном дефекта 1 для функции f(x)относительно сетки Dn наз. функцию S3(x)=S3(f; х), являющуюся многочленом третьей степени на каждом из отрезков [xk-1, xk], принадлежащую классу дважды непрерывно-дифференцируемых функций и удовлетворяющую условиям
При таком определении имеется еще два свободных параметра, для нахождения к-рых налагаются дополнительные краевые условия: Как непосредственно для задачи приближения функций, так и при решении других задач используются сплайны, к-рые в точках сетки Dn совпадают не только со значениями функций f(x), но и со значениями производных этой функции до нек-рого порядка. Часто при обработке эмпирических данных {yk} коэффициенты а i в Ln(x)определяются, исходя из требования минимизации суммы
Такое построение функции Ln(x)наз. интерполированием по методу наименьших квадратов. И. функций многих переменных имеет ряд принципиальных и вычислительных трудностей. Напр., в случае алгебраич. И. интерполяционный многочлен Лагранжа фиксированной степени, вообще говоря, не существует для произвольной системы различных узлов И. В частности, для функций двух переменных f(x, у )такой многочлен Ln(x, у )суммарной степени не выше и может быть построен по узлам (х k, yk )лишь при условии, что эти узлы не лежат на алгебраич. кривой порядка п. Другой подход к И. функций многих переменных f(xx,..., х т )состоит в том, что сначала интерполируется функция по переменной х 1 при фиксированных х k,/с=2, 3,..., т, потом по следующей переменной при фиксированных остальных х k и т. д. При таком способе построения интерполяционный алгебраич. многочлен Ln1...nm(x1, ..., х т )для функции f(x1 , ..., х т )с узлами
имеет вид j= 1, 2, ..., т,
где
Интерполяционные сплайны для функций многих переменных определяются на многомерной сетке при соответствующих изменениях по аналогии с одномерным случаем. И. функций используется для замены сложно вычисляемой функции другой, вычисляемой быстрее; для приближенного восстановления функции на всей области задания по значениям ее в отдельных точках; для получения сглаживающих функций., описывающих плавный процесс. Такого рода задачи имеют как самостоятельное значение, так и возникают в качестве вспомогательных при решении более сложных задач во многих областях науки и техники. И. функций применяется также для приближенного нахождения предельных значений функций, в задачах ускорения сходимости последовательностей и рядов и в других вопросах. Численное решение нелинейных уравнений и систем. Общие идеи построения интерполяционных методов решения уравнения f(x)=0 и систем уравнений fi(x1, x2,..., х т) = 0, i=1, 2,..., т, одни и те же. Трудности задачи И. функций многих переменных особенно сказываются при исследовании и практич. использовании такого рода методов для большого числа уравнений. В основу получения интерполяционных методов решения уравнения f(x)=0 положена замена функции f(х)ее интерполяционным полиномом L п (х)и последующим решением уравнения Ln(x)-0. Корни уравнения Ln(x)=0 берутся за приближенные решения уравнения f(х) = 0. Интерполяционный полином Ln(x)используется также при построении итерационных методов решения уравнения f(x) = 0. Напр., взяв за х п+1 корень линейного интерполяционного алгебраич. многочлена, построенного по значениям f(xn )и f'( х п )в узле х п, или по значениям f(xn-1) и f(xn )в узлах х п-1 и xn приходят соответственно к методам Ньютона и секущих:
где f(xn-1, х п)- разделенная разность функции f(x)для узлов xn-1 и х п. При выполнении нек-рых условий последовательность значений х п будет стремиться при
Предполагается, что обратная функция существует в окрестности искомого корня уравнения f(х)=0 и составлена таблица значений xk и yk =f(xk), k=0, 1, ..., п. За следующее приближенное значение xk+1 принимается значение интерполяционного многочлена в нуле:
Численное интегрирование. Аппарат И. функций лежит в основе построения многих квадратурных и кубатурных формул. Такого рода формулы строятся путем замены интегрируемой функции на всей области или на ее составных частях интерполяционными полиномами того или иного вида и последующим интегрированием этих полиномов. Напр., квадратурные формулы наивысшей алгебраич. степени точности, так наз. Гаусса квадратурные формулы
где р(х)- знакопостоянная весовая функция, получаются в результате замены функции f(x)интерполяционным алгебраич. многочленом, построенным по корням xk ортогонального относительно веса р(х)многочлена степени п. Если разделить весь отрезок интегрирования [ а, b]на четное число правных частей длины
где fk=f(a+kh), k=0,1, . . ., п. Можно взять за основу и интерполяционные сплайны какой-то фиксированной степени. Изложенная выше схема построения формул для приближенного вычисления интегралов применима и в многомерном случае. Численное дифференцирование. Формулы численного дифференцирования получаются в результате дифференцирования интерполяционных формул. При этом, как правило, заранее известна нек-рая априорная информация о дифференцируемой функции, касающаяся ее гладкости. Пусть Ln(x)- интерполяционный полином нек-рого вида для функции f(x),a Rn(x)- остаток интерполяционной формулы:
Если в равенстве
пренебречь величиной R п(i) (х), то это приведет к формуле для приближенного вычисления i-й производной функции f(x):
Формулы численного дифференцирования, в основе к-рых лежит И., получаются из приближенного равенства (3) в зависимости от выбора интерполяционного полинома Ln(x). При численном дифференцировании используются, как правило, приближенные значения функции в узлах; погрешность формул численного дифференцирования зависит не только от способа И. и шага И., но и от ошибки используемых значений функции в узлах. Напр., в случае линейного И. (1):
причем для остатка R'1(x)имеет место представление:
Если f(xk+1) и f(х k )известны соответственно с погрешностями ek+1 и Численное решение интегральных уравнений. Неизвестная функция ,j(х)заменяется в интегральном уравнении какой-либо интерполяционной формулой (интерполяционным полиномом,, интерполяционным сплайном и т. д.) с узлами И. х k, а приближенные значения для j( х k )находятся из системы, полученной после подстановки вместо независимой переменной хузлов И. xk. Напр., для линейного интегрального уравнения Фредгольма 2-го рода
можно воспользоваться лагранжевым представлением интерполяционного многочлена:
где Rn(x)- остаток И., Замена функции j(х)в (5) ее интерполяционным многочленом Ln(x)и хна х i, приводит к линейной системе уравнении
для нахождения приближенных значений ji решения j(x)уравнения (5) в узлах xi. В случае нелинейных интегральных уравнений приближенные значения ji находятся соответственно из нелинейной системы. Численное решение дифференциальных уравнений. Построение численных методов решения дифференциальных уравнений состоит в замене производных искомых функций интерполяционными формулами численного дифференцирования, а в ряде случаев и заменой интерполяционными формулами других функций и выражений, входящих в уравнения. Пусть имеются формулы численного дифференцирования
для равноотстоящих узлов xk= х 0+kh, получаемые соответственно дифференцированием формул линейной и квадратичной И. (1) и (2). Тогда для обыкновенного дифференциального уравнения 2-го порядка
при нек-рых дополнительных условиях получается с учетом (6) уравнение в конечных разностях
из к-рого вместе с уравнениями, полученными из дополнительных условий, находятся приближенные значения yk решения у(х)в узлах х k. Сведение дифференциальных уравнений с частными производными к соответствующим уравнениям в конечных разностях производится часто также с использованием формул численного дифференцирования. Интерполяционный метод применим для решения дифференциальных уравнений, записанных в интегральной форме. Напр., для нахождения приближенного решения задачи Коши
в точках xk = x0+kh, k= 0, 1, . .., используются разностные формулы типа
получаемые заменой функции под знаком интеграла в равенстве
интерполяционным полиномом и последующим интегрированием. В частности, таким образом получены формулы Адамса для уравнения 1-го порядка (7) формулы Стёрмера для уравнений 2-го порядка и т. д. Такой подход позволяет, строить вычислительные алгоритмы для широкого класса дифференциальных уравнений в том числе и для уравнений в частных производных. Исследование разрешимости, точности и устойчивости решения возникающих конечно разностных уравнений представляет собой основную и наиболее трудную часть теории численного решения дифференциальных уравнений. Интерполирование операторов и некоторые общие подходы к построению численных методов. Построение численных методов решения математич. задач, записанных в виде у=Ах, где элементы хи у принадлежат нек-рым множествам Xи Y, а А- заданный оператор, состоит в замене множеств Xи Y и оператора Аили только нек-рых из этих трех объектов другими, удобными для вычислительных целей. При этом замена должна быть сделана так, чтобы решение новой задачи
rge х 0 и х 1 - узлы И., F(x0, x1)- оператор разделенной разности 1-го порядка, определяемый как линейный оператор, удовлетворяющий условию
Данное определение оператора разделенной разности в ряде случаев конкретизируется. С использованием линейного И. (8) "метод секущих" для уравнения F(x)=0 записывается в виде
тде F-1(xn-1, xn)- оператор, обратный к F(xn_x, xn). Постановка задачи И. функционалов, представляющая интерес для теории приближенных методов такова. Пусть {yi(x)}, i=0, 1, . . ., п,- некоторые фиксированные функционалы или классы функционалов, определенные на X. Функционал Ln[F; x]наз. интерполяционным функциональным многочленом для данного функционала F(x)и системы точек {xk}из X, если выполняются соотношения
И. функционалов используется при построении приближенных методов вычисления континуальных интегралов, для нахождения экстремальных значений функционалов и ряда других задач. Напр., приближенные интерполяционные формулы для вычисления континуальных интегралов имеют вид
при этом интеграл от интерполяционного полинома Ln[F; x]для нек-рых мер m может вычисляться точно или сводиться к конечномерным интегралам. Интерполяционный полином L1[F; x], когда Xесть пространство непрерывных на отрезке [ а, b]функций С[ а, b], представляется в виде интеграла Стилтьеса
где x0(t)и x1(t)- узлы И., а функция
Если F(x)- постоянный или линейный функционал, то LX[F; x]=F(x). Применение И. к нахождению экстремальных значений функционалов может быть проиллюстрировано двумя интерполяционными аналогами метода градиента для нахождения локальной точки безусловного минимума функционала F(x), определенного на нек-ром гильбертовом пространстве. Первый из этих методов получается, если в градиентном методе заменить grad F(xn )на F(xn-1, xn), т. е.
Второй метод использует градиент интерполяционного полинома. По приближениям xn-2, xn-1, х п к экстремальной точке х* функционала F(x)строится квадратичный интерполяционный функционал
где F(xn-2, х n-1, х п)- разделенная разность 2-го порядка функционала F(x)относительно узлов х n-2, х n-1 х п, и новое приближение х п+1 находится по формуле
Итерационные методы (9) и (10) используют соответственно два и три начальных приближения. Применение И. функционалов и операторов для построения вычислительных алгоритмов решения конкретных задач основано на использовании интерполяционных формул с малой величиной погрешности. Такого рода формулы должны строиться для отдельных классов функционалов и операторов с учетом специфики этих классов. Лит.:[1] Гончаров В. Л., Теория интерполирования и приближения функций, 2 изд., М., 1954; [2], Березин И. С., Жидков Н. П., Методы вычислений, т. 1-2, М., 1959-60; [3) Бахвалов Н. С, Численные методы, 2 изд., М., 1975; [4] Крылов В. I., Бобков В. В., Монастырный П. И., Вычислительные методы, т. 1 -2 М., 1976-77; [5] Стечкин С. Б., Субботин Ю. Н., Сплайны в вычислительной математике, М., 1976; [6] Самарский А. А., Введение в теорию разностных схем, М., 1971; [7] Янович Л. А., Приближенное вычисление континуальных интегралов по гауссовым мерам, Минск, 1976. Л. <А. Янович |
|
|
|

 означает построение другой функции Ln(x)=Ln(f; x )такой, что L п( х k)=f(xk), k=0,1, ..., п. В более общей постановке задача И. функции f(x). состоит в построении Ln(x)не только из условия совпадения значений функций Ln(x)и f(х)на сетке Dn, но и из требования совпадения в отдельных узлах их производных до какого-то порядка или нек-рых других соотношений, связывающих f(х)и L п (х).
означает построение другой функции Ln(x)=Ln(f; x )такой, что L п( х k)=f(xk), k=0,1, ..., п. В более общей постановке задача И. функции f(x). состоит в построении Ln(x)не только из условия совпадения значений функций Ln(x)и f(х)на сетке Dn, но и из требования совпадения в отдельных узлах их производных до какого-то порядка или нек-рых других соотношений, связывающих f(х)и L п (х).
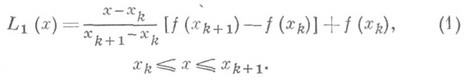
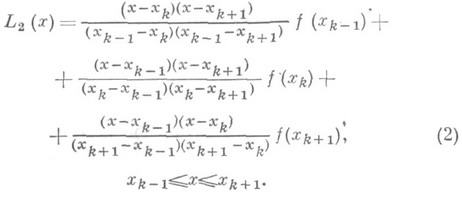
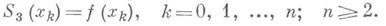
 i=l,2;S'3(a)= а п и
i=l,2;S'3(a)= а п и  или нек-рые другие.
или нек-рые другие.


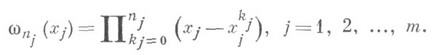

 к решению уравнения f(x)=0. Другой подход к построению методов решения уравнения f(x)=0 основан на И. обратной функции х=g(y). Пусть в качестве интерполяционной формулы для функции x=g(y)взят интерполяционный алгебраич. многочлен Лагранжа
к решению уравнения f(x)=0. Другой подход к построению методов решения уравнения f(x)=0 основан на И. обратной функции х=g(y). Пусть в качестве интерполяционной формулы для функции x=g(y)взят интерполяционный алгебраич. многочлен Лагранжа

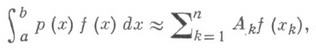
 и на каждом сдвоенном частичном отрезке заменить f(х)ее квадратичным интерполяционным многочленом с узлами в крайних и средней точках, то придем к составной Симпсона формуле
и на каждом сдвоенном частичном отрезке заменить f(х)ее квадратичным интерполяционным многочленом с узлами в крайних и средней точках, то придем к составной Симпсона формуле
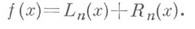




 то погрешность формулы (4) будет содержать еще член (ek+1-ek)/h, к-рый с уменьшением шага hвозрастает. При использовании формул численного дифференцирования шаг И. должен согласовываться с погрешностью значений функции. Поэтому на практике нередки случаи, когда известная с нек-рой погрешностью на густой сетке функция используется в данной задаче не во всех точках, а на более редкой сетке.
то погрешность формулы (4) будет содержать еще член (ek+1-ek)/h, к-рый с уменьшением шага hвозрастает. При использовании формул численного дифференцирования шаг И. должен согласовываться с погрешностью значений функции. Поэтому на практике нередки случаи, когда известная с нек-рой погрешностью на густой сетке функция используется в данной задаче не во всех точках, а на более редкой сетке.





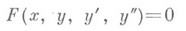


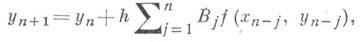
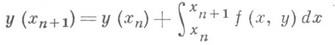
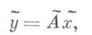 состоящей в нахождении
состоящей в нахождении  или
или  было в каком-то смысле близко к решению первоначальной задачи. Один из способов замены оператора Аего приближением
было в каком-то смысле близко к решению первоначальной задачи. Один из способов замены оператора Аего приближением  состоит в использовании интерполирования операторов. Имеются различные формулировки задачи И" операторов. Линейный интерполяционный оператор L1(F; x )для данного оператора записывается в виде
состоит в использовании интерполирования операторов. Имеются различные формулировки задачи И" операторов. Линейный интерполяционный оператор L1(F; x )для данного оператора записывается в виде