|
"
0
C
F
G
H
K
L
N
P
S
T
W
Z
А
Б
В
Г
Д
Е
Ж
З
И
Й
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Ш
Э
Ю
Я
АНАЛИТИЧЕСКАЯ ФУНКЦИЯ АБСТРАКТНАЯЗначение АНАЛИТИЧЕСКАЯ ФУНКЦИЯ АБСТРАКТНАЯ в математической энциклопедии: аналитическое отображение банаховых пространств,- функция где Другой подход к понятию А. ф. а. возникает из дифференцируемости по Гато. Функция f(x).из Dв Yназ. слабо аналитической в D, илп дифференцируемой по Гато в D, если для каждого линейного непрерывного функционала у' над пространством Yи каждого элемента Термин "А. ф. а." иногда используется в более узком смысле, когда под ним понимается функция пространстве Y. В этом случае всякая слабо аналитич. функция где ряд сходится по норме и Функция у=Р (х).из Xв Yназ. полиномом относительно переменного хстепени не выше т, если для всех где функции На А. ф. а. переносятся с соответственными изменениями многие основные результаты классич. теории аналитич. функций такие, как максимума модуля принцип, теоремы единственности, Витали теорема, Лиувил. <ля теорема и др. Множество всех А. ф. а. в области Dобразует линейное пространство. Понятие А. ф. а. обобщается и на более широкие классы пространств Xи Y, напр, на локально выпуклые топологич. пространства, банаховы пространства над произвольным полным нормированным полем и т. <д. Лит.: [1] Xилле Э., Филлипс Р., Функциональный анализ и полугруппы, пер. с англ., 2 изд., М., 1962; [2] Эдвардс Р.-Э., Функциональный анализ. Теория и приложения, пер. с англ., М., 1969; [3] Шварц Л., Анализ, пер. с англ., Т. 2, М., 1972. А. А. Данилееич, Е. Д. Коломенцев. |
|
|
|

 действующая из нек-рой области Dбанахова пространства Xв банахово пространство Y и дифференцируемая по Фреше всюду в D, т. е. такая, что для каждой точки
действующая из нек-рой области Dбанахова пространства Xв банахово пространство Y и дифференцируемая по Фреше всюду в D, т. е. такая, что для каждой точки  существует ограниченный линейный оператор
существует ограниченный линейный оператор  из
из  , для к-рого выполняется соотношение:
, для к-рого выполняется соотношение:
 обозначает норму в
обозначает норму в 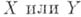 ;
;  наз. дифференциалом Фреше функции f в точке а.
наз. дифференциалом Фреше функции f в точке а. комплексная функция
комплексная функция  является голоморфной функцией комплексного переменного
является голоморфной функцией комплексного переменного  в круге
в круге 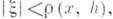 где
где  Всякая А. ф. а. в области Dнепрерывна и слабо аналитична в D. Обратное также верно, причем условие непрерывности можно заменить локальной ограниченностью или непрерывностью по Бэру.
Всякая А. ф. а. в области Dнепрерывна и слабо аналитична в D. Обратное также верно, причем условие непрерывности можно заменить локальной ограниченностью или непрерывностью по Бэру. комплексного переменного
комплексного переменного  со значениями в банаховом или даже линейном локально выпуклом топологич.
со значениями в банаховом или даже линейном локально выпуклом топологич. в области Dплоскости комплексного переменного
в области Dплоскости комплексного переменного  является А. ф. а. Можно также сказать, что функция
является А. ф. а. Можно также сказать, что функция  будет А. ф. а. в области
будет А. ф. а. в области  тогда и только тогда, когда
тогда и только тогда, когда 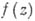 непрерывна в
непрерывна в 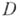 и для любого простого замкнутого спрямляемого контура
и для любого простого замкнутого спрямляемого контура  интеграл
интеграл  обращается в нуль. Для А. ф. а.
обращается в нуль. Для А. ф. а. 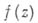 комплексного переменного z справедлива интегральная формула Кошп (см. Коши интеграл). Пусть
комплексного переменного z справедлива интегральная формула Кошп (см. Коши интеграл). Пусть 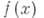 - слабо аналитич. функция в области Dбанахова пространства X. Тогда
- слабо аналитич. функция в области Dбанахова пространства X. Тогда 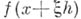 , как функция комплексного переменного
, как функция комплексного переменного  , имеет производные всех порядков в области
, имеет производные всех порядков в области  причем эти производные суть А. ф. а. из D в Y. Если множество
причем эти производные суть А. ф. а. из D в Y. Если множество 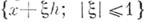 принадлежит D, то
принадлежит D, то 

 и для всех комплексных
и для всех комплексных 
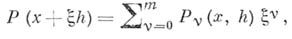
 не зависят от
не зависят от  . Степень
. Степень  точно равна т, если
точно равна т, если 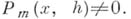 Степенным рядом наз. ряд вида
Степенным рядом наз. ряд вида  - однородные полиномы степени птакие, что
- однородные полиномы степени птакие, что 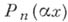 =
= для всех комплексных
для всех комплексных  . Всякий слабо сходящийся степенной ряд
. Всякий слабо сходящийся степенной ряд  в области Dсходится и по норме к нек-рой слабо аналитической функции
в области Dсходится и по норме к нек-рой слабо аналитической функции  , причем
, причем 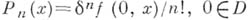 . Функция
. Функция  является А. ф. а. в Dтогда и только тогда, когда в окрестности каждой точки
является А. ф. а. в Dтогда и только тогда, когда в окрестности каждой точки 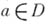 она разлагается в степенной
она разлагается в степенной  ряд где все
ряд где все  непрерывны в X.
непрерывны в X.