|
"
0
C
F
G
H
K
L
N
P
S
T
W
Z
А
Б
В
Г
Д
Е
Ж
З
И
Й
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Ш
Э
Ю
Я
ИНТЕГРАЛЬНОЕ ПРЕОБРАЗОВАНИЕЗначение ИНТЕГРАЛЬНОЕ ПРЕОБРАЗОВАНИЕ в математической энциклопедии: - функциональное преобразование вида
где С- конечный или бесконечный контур в комплексной плоскости, К( х, t)- ядро И. п. Наиболее часто рассматриваются И. п., для которых K(x,t)=K(xt )и С- действительная ось или ее часть ( а, b). Если И. п. Формулы, позволяющие восстановить функцию f(t)по известной F(x), наз. формулами обращения И. п. Примеры И. п. Преобразование Бохнера:
где Jv (х)- функция Бесселя 1-го рода порядка v, р - расстояние в Rn. Формула обращения: f= T2f. Равенство Парсеваля:
Преобразование Вебера:
где
При а->0 преобразование Вебера переходит в преобразование Ганкеля:
При v==±1/2 это преобразование сводится к синус- и косинус-преобразованиям Фурье. Формула обращения: если
Равенство Парсеваля: если
Другие формы преобразования Ганнеля:
Преобразование Вейерштрасса:
является частным случаем свертки преобразования. Цепные преобразования. Пусть
причем fn+1(x)=f1(x). Такая последовательность И. п. наз. цепочкой И. п. При n=2 цепные И. п. часто наз. преобразованиями Фурье. Кратные (многомерные) И. п.- преобразования вида (1), где t, И. п. обобщенных функций могут быть построены следующими основными способами: 1) Строится пространство основных функций U, содержащее ядро К( х, t )рассматриваемого И. п. Т. Преобразование Tf для любой обобщенной функции
2) Строится пространство основных функций U, на к-ром определено классическое И. п. Т, отображающее Uна нек-рое пространство основных функций V. И. п. T'f обобщенной функции 3) Рассматриваемое И. п. выражается через другое И. п., к-рое определено для обобщенных функций. См. также ст. Ватсона преобразование, Гаусса преобразование, Гегенбауэра преобразование, Конторовича- Лебедева преобразование, Мейера преобразование, Мелера- Фока преобразование, Меллина преобразование. Свертки преобразование, Стилтьеса преобразование, Уиттекера преобразование, Фурье преобразование, Харди преобразование, Эйлера преобразование, Эрмита преобразование, Якоби преобразование. Лит.:[1] Диткин В. А., Прудников А. П., в сб.: "Итоги науки. Математический анализ. 1966", М., 1967, с. 7-82; [2] Брычков Ю. А., Прудников А. П., Интегральные преобразования обобщенных функций, М., 1977; [3] Владимиров В. С, Обобщенные функции в математической физике, М., 1976. Ю. А. Брычков, А. П. Прудников. |
|
|
|

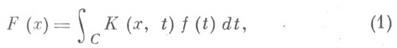
 то И. п. наз. конечным
то И. п. наз. конечным


 Yv(x).- функции Бесселя 1-го и 2-го рода. Формула обращения:
Yv(x).- функции Бесселя 1-го и 2-го рода. Формула обращения:

 f(t)имеет ограниченную вариацию в окрестности точки t0>0 и
f(t)имеет ограниченную вариацию в окрестности точки t0>0 и  то
то
 F(x)п G(x)- преобразования Ганкеля функций f(t)и g{t), причем f,
F(x)п G(x)- преобразования Ганкеля функций f(t)и g{t), причем f,  то
то

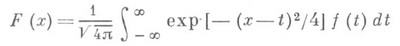

 С- некоторая область n-мерного комплексного евклидова пространства.
С- некоторая область n-мерного комплексного евклидова пространства. определяется как значение функционала f на основной функции К( х, t). формулой
определяется как значение функционала f на основной функции К( х, t). формулой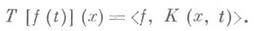
 вводится равенством
вводится равенством 