|
"
0
C
F
G
H
K
L
N
P
S
T
W
Z
А
Б
В
Г
Д
Е
Ж
З
И
Й
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Ш
Э
Ю
Я
ИНТЕГРАЛЬНОЕ ИСЧИСЛЕНИЕЗначение ИНТЕГРАЛЬНОЕ ИСЧИСЛЕНИЕ в математической энциклопедии: - раздел математики, в к-ром изучаются понятия интеграла, его свойства и методы вычислений. И. и. непрерывно связано с дифференциальным исчислением и составляет вместе с ним основу математич. анализа. Истоки И. и. относятся к античному периоду развития математики и связаны с исчерпывания методом, разработанным математиками Древней Греции. Этот метод возник при решении задач на вычисление площадей плоских фигур и поверхностей, объемов тел, нек-рых задач статики и гидродинамики. Он основан на аппроксимации рассматриваемых объектов ступенчатыми фигурами или телами, составленными из простейших фигур или пространственных тел (прямоугольников, параллелепипедов, цилиндров и т. п.). В этом смысле метод исчерпывания можно рассматривать как античный интегральный метод. Наибольшее развитие метод исчерпывания в древнюю эпоху получил в работах Евдокса (4 в. до н. э.) и особенно Архимеда (3 в. до н. э.). Дальнейшее его применение и совершенствование связано с именами многих ученых 15 - 17 вв. Основные понятия и теория интегрального и дифференциального исчислений, прежде всего связь операций дифференцирования и интегрирования, а также их применения к решению прикладных задач, были разработаны в трудах И. Ньютона (I. Newton) н Г. Лейбница (G. Leibniz) в конце 17 в. Их исследования явились началом интенсивного развития математич. анализа. Существенную роль в его создании в 18 в. сыграли работы Л. Эйлера (L. Euler), Я. и И. Бернулли (Jacob, Johann Bernoulli), Ж. Лагранжа (J. Lagrange). В 19 в. в связи с появлением понятия предела И. и, приобрело логически завершенную форму [работы О. Коши (А. Саuchy), Б. Римана (В. Riemann) и др. Разработка теории и методов И. и. происходила в конце 19 в. и в 20 в. одновременно с исследованиями по теории меры, играющей существенную роль в И. и. С помощью И. и. стало возможным решать единым методом многие теоретич. и прикладные задачи, как новые, к-рые ранее не поддавались решению, так и старые, требовавшие прежде специальных искусственных приемов. Основными понятиями И. и. являются два тесно связанных понятия интеграла: неопределенного и определенного. Неопределенный интеграл от данной действительной функции на нек-ром промежутке определяется как совокупность всех ее первообразных на этом промежутке, т. е. функций, производные к-рых совпадают с заданной функцией. Неопределенный интеграл от функции f(x)обозначается через
Операция нахождения неопределенного интеграла наз. интегрированием. Интегрирование является операцией, обратной к операций дифференцирования:
Операция интегрирования линейна: если на нек-ром промежутке существуют неопределенные интегралы
то для любых действительных чисел l1 и l2 на том же промежутке существует интеграл
Для неопределенных интегралов справедлива формула интегрирования по частям:если функции и(х)и v(x). дифференцируемы на нек-ром промежутке и интеграл
Справедлива формула замены переменного: если для функций f(x)и x=j(t), определенных на нек-рых промежутках, имеет смысл сложная функция f[j(t)], функция j(t)дифференцируема и существует интеграл
(см. Интегрирование подстановкой). Всякая непрерывная на нек-ром промежутке функция имеет на нем первообразную и, следовательно, для нее существует неопределенный интеграл. Задача фактического нахождения неопределенного интеграла от конкретно заданной функции осложняется тем, что неопределенный интеграл от элементарной функции не является, вообще говоря, элементарной функцией. Известны многие классы функций, для к-рых оказывается возможным выразить их неопределенные интегралы через элементарные функции. Простейшими примерами этого являются интегралы, к-рые получаются из таблицы производных основных элементарных функций (см. Дифференциальное исчисление):
Если знаменатель подинтегральной функции обращается в нуль в нек-рой точке, то написанные формулы справедливы лишь для тех промежутков, в к-рых не происходит обращения в нуль указанного знаменателя (см. формулы 1, 2, 6, 7, 11, 13, 15). Неопределенный интеграл от рациональной функции на всяком промежутке, на к-ром знаменатель не обращается в нуль, является суперпозицией рациональных функций, арктангенсов и натуральных логарифмов. Нахождение алгебраич. части неопределенного интеграла от рациональной функции может быть осуществлено Остроградского методом. К интегрированию рациональных функций с помощью подстановок сводятся, напр., интегралы вида
где r1, r2,..., rm- рациональные числа, интегралы вида
(см. Эйлера подстановки), нек-рые случаи интегралов от дифференциальных биномов, интегралы вида
(здесь везде R(y1, y2, ..., у п)- рациональные функции), интегралы
и мн. др. Вместе с тем, напр., интегралы
не выражаются через элементарные функции. Определенным интегралом
от функции f(x), заданной на отрезке [ а, b], наз. предел интегральных сумм определенного вида (см. Коши интеграл, Римана интеграл, Лебега интеграл, Колмогорова интеграл, Стилтъеса интеграл и т. д.). Если этот предел существует, функцию f(x)наз. интегрируемой соответственно по Коши, по Риману, по Лебегу и т. д. Геометрич. смысл интеграла связан 4 с понятием площади: если функция
равно площади криволинейной трапеции, образованной графиком функции f(x), т. е. множеством, граница к-рого состоит из графика функции f(x), Определенный интеграл обладает свойством линейности: если функции f1 (х)и f2 (х)интегрируемы на отрезке [ а, b], то для произвольных действительных чисел l1 и l2 функция
Интегрируемость функции на отрезке обладает свойством монотонности: если функция f(х)интегрируема на отрезке [ а, b]и
Если функции f(x)и g(x)интегрируемы, то их произведение также интегрируемо. Если
Если функция f(x)интегрируема на [ а, b], то ее абсолютная величина |f(x)|также интегрируема на [ а, b]и
По определению полагают
Для определенных интегралов справедливы теоремы о среднем. Напр., если f(x)и g(x)интегрируемы на отрезке [ а, b],
При дополнительном предположении непрерывности на отрезке [ а, b]функции f(x)на интервале ( а, b )существует такая точка x, что
В частности, если g(x)=A, то
Интегралы с переменным верхним пределом. Если функция f(x)интегрируема по Риману на отрезке [ а, b], то функция
непрерывна на этом отрезке. Если, кроме того, функция f(x)непрерывна в точке х 0, то функция F(x)дифференцируема в этой точке и F'(x0) = f(x0). Иначе говоря, в точках непрерывности функции справедлива формула
Следовательно, для всякой интегрируемой по Риману на отрезке [ а, b]функции эта формула справедлива во всех точках, кроме, быть может, множества точек, имеющих меру Лебега, равную нулю, ибо если функция интегрируема по Риману на некотором отрезке, то множество ее точек разрыва имеет меру нуль. Таким образом, если функция f(x)непрерывна на отрезке [ а, b], то функция Геометрия, смысл этой связи состоит в том, что задача о нахождении касательной к кривой и вычисление площадей плоских фигур являются в указанном смысле взаимно обратными. Для любой первообразной F(x)непрерывной функции f(x)на отрезке [ а, b]имеет место формула Ньютона - Лейбница:
Она показывает, что определенный интеграл по некоторому отрезку от непрерывной функции равен разности значений на концах этого отрезка любой из ее первообразных. Эту формулу иногда принимают за определение определенного интеграла. В этом случае доказывается, что введенный таким образом интеграл Для определенных интегралов справедливо правило замены переменного и формула интегрирования по частям. Пусть, напр., функция f(х) непрерывна на интервале (а, b)и функция j(t)непрерывна вместе со своей производной j' (t)на интервале (a, b), причем интервал (a, b) отображается с помощью функции j(t) в интервал (a, b): a<j(t)<b при a<t<b и, следовательно, на (a,b) имеет смысл суперпозиция f[j(t)]. Тогда, если
Формула интегрирования по частям:
где функции и(х)и v(x)имеют на отрезке [ а, b]интегрируемые производные. Формула Ньютона - Лейбница сводит вычисление определенного интеграла к отысканию значений его первообразной. Поскольку задача отыскания первообразной является сама по себе сложной, то большое значение имеют другие методы нахождения определенных интегралов, среди к-рых прежде всего следует отметить , метод вычетов и метод дифференцирования и интегрирования по параметру зависящих от параметров интегралов. Разрабатываются также численные методы приближенного вычисления интегралов. Обобщение понятия интеграла на случай неограниченных функций и случай неограниченного промежутка приводит к понятию несобственного интеграла, к-рый определяется при помощи еще одного дополнительного предельного перехода. Понятия неопределенного и определенного интегралов переносятся на комплекснозначные функции. Представление любой регулярной функции комплексного переменного в виде Коши интеграла по контуру сыграло важную роль в развитии теории аналитич. функций. Обобщение понятия определенного, интеграла от функции одного переменного на случай функций многих переменных приводит к понятию кратного интеграла. Для неограниченных множеств и неограниченных функций многих переменных, также как и в одномерном случае, вводится понятие несобственного интеграла. Расширение практич. использования И. и. обусловило введение понятий криволинейного интеграла- интеграла по кривой, поверхностного интеграла- интеграла по поверхности и вообще - интеграла по многообразиям, сводимых в нек-ром смысле к определенному интегралу (криволинейный интеграл - к интегралу по отрезку, поверхностный - к интегралу по области (плоской), интеграл по n-мерному многообразию - к интегралу по n-мерной области). Интегралы по многообразиям, в частности криволинейные и поверхностные, играют важную роль в И. и. функций многих переменных; с их помощью можно установить связь между интегрированием по области и ее границе или, в общем случае, по многообразию и его краю. Эта связь устанавливается Стокса формулой (см. также Остроградского формула, Грина формулы), являющейся обобщением на многомерный случай формулы Ньютона - Лейбница. Кратные, криволинейные и поверхностные интегралы находят непосредственное применение в математич. физике, в частности в теории поля. Кратные интегралы и связанные с ними понятия широко используются при решении конкретных прикладных задач. Для численного вычисления кратных интегралов разработана теория кубатурных формул. Теория и методы И. и. числовых функций конечного числа переменных переносятся и на более общие объекты. Напр., теория интегрирования функций, значения к-рых принадлежат линейным нормированным пространствам, функций, заданных на топологич. группах, обобщенных функций и функций бесконечного числа переменных (континуальный интеграл). Наконец, новое направление И. и. связано также с появлением и развитием конструктивной математики. И. и. применяется во многих разделах математики (в теории дифференциальных и интегральных уравнений, в теории вероятностей и математич. статистике, в теории оптимальных процессов и др.), и в ее приложениях. Лит.:см. [1] - [24] при статье Дифференциальное исчисление, а также дополнение к разделу "Работы основоположников и классиков...": [25] Архимед, Сочинения, М., 1962; [26] Кеплер И., Новая стереометрия винных бочек, [пер. с латин.], М.- Л., 1934; [27] Кавальери Б., Геометрия..., [пер. с латин.], М.- Л., 1940; [28] Эйлер Л., Интегральное исчисление, пер. с латин., т. 1 - 3, М., 1956-58. Л. Д. Кудрявцев. |
|
|
|

 Если F(x)- какая-либо первообразная функцияf(x), то любая другая ее первообразная имеет вид F(x)+C, где С- произвольная постоянная, поэтому пишут
Если F(x)- какая-либо первообразная функцияf(x), то любая другая ее первообразная имеет вид F(x)+C, где С- произвольная постоянная, поэтому пишут



 существует, то существует и интеграл
существует, то существует и интеграл  причем имеет место равенство
причем имеет место равенство
 то существует и интеграл
то существует и интеграл







 непрерывна на отрезке [а, b], то значение интеграла
непрерывна на отрезке [а, b], то значение интеграла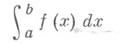
 . отрезка [ а, b]и двух отрезков прямых х=а и x=b, к-рые могут вырождаться в точки. К задаче вычисления предела интегральных сумм, т. е. нахождению определенного интеграла, сводится вычисление многих встречающихся на практике величин: площадей фигур и поверхностей, объемов тел, работы силы, координат центра тяжести, значений моментов инерции различных тел и т.. п.
. отрезка [ а, b]и двух отрезков прямых х=а и x=b, к-рые могут вырождаться в точки. К задаче вычисления предела интегральных сумм, т. е. нахождению определенного интеграла, сводится вычисление многих встречающихся на практике величин: площадей фигур и поверхностей, объемов тел, работы силы, координат центра тяжести, значений моментов инерции различных тел и т.. п. также интегрируема на отрезке и
также интегрируема на отрезке и
 то функция f(х)интегрируема и на отрезке [ с, d]. Справедливо свойство аддитивности интеграла относительно отрезков, по к-рым происходит интегрирование: если а<с<b и функция f(x)интегрируема на отрезках [ а, с]и [ с, b], то она интегрируема и на отрезке [ а, b], причем
то функция f(х)интегрируема и на отрезке [ с, d]. Справедливо свойство аддитивности интеграла относительно отрезков, по к-рым происходит интегрирование: если а<с<b и функция f(x)интегрируема на отрезках [ а, с]и [ с, b], то она интегрируема и на отрезке [ а, b], причем
 на [ а, b], то
на [ а, b], то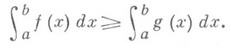

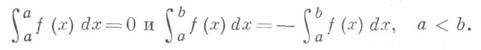
 и функция g(x)не меняет знака на отрезке [ а, b], т. е. либо неотрицательна, либо неположительна на этом отрезке, то существует такое число
и функция g(x)не меняет знака на отрезке [ а, b], т. е. либо неотрицательна, либо неположительна на этом отрезке, то существует такое число  что
что




 является ее первообразной на этом отрезке. Эта теорема показывает, что операция дифференцирования является обратной к взятию определенного интеграла с переменным верхним пределом, тем самым устанавливая связь между определенным и неопределенным интегралами:
является ее первообразной на этом отрезке. Эта теорема показывает, что операция дифференцирования является обратной к взятию определенного интеграла с переменным верхним пределом, тем самым устанавливая связь между определенным и неопределенным интегралами:

 является пределом соответствующих сумм.
является пределом соответствующих сумм.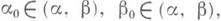 то имеет место формула замены переменного
то имеет место формула замены переменного
