"
0
C
F
G
H
K
L
N
P
S
T
W
Z
А
Б
В
Г
Д
Е
Ж
З
И
Й
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Ш
Э
Ю
Я
АНАЛИТИЧЕСКАЯ ТЕОРИЯ ЧИСЕЛ
Значение АНАЛИТИЧЕСКАЯ ТЕОРИЯ ЧИСЕЛ в математической энциклопедии:
- раздел теории чисел. В А. т. ч. включают вопросы распределения простых чисел, аддитивные проблемы, исследование поведения теоретико-числовых функций, теорию алгебраических и трансцендентных чисел.
Распределение простых чисел, а) Одной из интереснейших и труднейших задач А. т. ч. является проблема распределения простых чисел (п. ч.). Первый результат в проблеме распределения п. ч.- теорема Евклида: п. ч. бесконечно много. Пусть (х) - число п. ч., не превосходящих х;тогда теорема Евклида может быть сформулирована так:  при
при 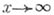 . Следующий шаг в этом вопросе был сделан П. Л. Чебышевым (1850). Он доказал, что:
. Следующий шаг в этом вопросе был сделан П. Л. Чебышевым (1850). Он доказал, что:
1) Для величины 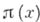 выполняются неравенства
выполняются неравенства

причем 
2) Если существует предел  то этот предел равен 1.
то этот предел равен 1.
Проблему существования последнего предела решили в 1896 Ж. Адамар (J. Hadamard) и Ш. Ж. Ла Балле Пуссен (Ch. J. La Vallee Poussin), установив тем самым, что

Ш. Ж. Ла Балле Пуссен доказал значительно больше, а именно: пусть

тогда

где 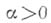 - абсолютная постоянная (см. Балле Пуссена теорема). При решении этой проблемы были использованы методы теории функций комплексного переменного. С проблемой оценки
- абсолютная постоянная (см. Балле Пуссена теорема). При решении этой проблемы были использованы методы теории функций комплексного переменного. С проблемой оценки  тесно связана проблема поведения нек-рой функции комплексного переменного, к-рую впервые (1859) изучал Б. Риман (В. Riemann), и к-рая теперь наз. Рпмана дзета-функцией. Эта функция задается равенством
тесно связана проблема поведения нек-рой функции комплексного переменного, к-рую впервые (1859) изучал Б. Риман (В. Riemann), и к-рая теперь наз. Рпмана дзета-функцией. Эта функция задается равенством

При действительном s дзета-функцию рассматривал еще Л. Эйлер (L. Euler; 1737, 1749) и им было доказано тождество, к-рое указывает на связь  с п. ч.:
с п. ч.:

где произведение берется по всем п. ч. Функцию  , заданную рядом при
, заданную рядом при  , можно аналитически продолжить на всю плоскость комплексного переменного; тогда получится функция, к-рая будет аналитической на всей плоскости комплексного переменного за исклю-.ченпем точки
, можно аналитически продолжить на всю плоскость комплексного переменного; тогда получится функция, к-рая будет аналитической на всей плоскости комплексного переменного за исклю-.ченпем точки  , где она имеет простой полюс с вычетом, равным 1. Проблема оценки остатка
, где она имеет простой полюс с вычетом, равным 1. Проблема оценки остатка  в асимптотич. формуле распределения п. ч. тесно связана с проблемой распределения нулей
в асимптотич. формуле распределения п. ч. тесно связана с проблемой распределения нулей  в "критической" полосе
в "критической" полосе 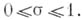 Б. Риманом была высказана гипотеза, что все нули
Б. Риманом была высказана гипотеза, что все нули  в критич. полосе лежат на прямой
в критич. полосе лежат на прямой 
 Из этой гипотезы следует, что
Из этой гипотезы следует, что  Наоборот, из соотношения
Наоборот, из соотношения  - произвольно мало, следует справедливость Римана гипотезы о нулях
- произвольно мало, следует справедливость Римана гипотезы о нулях  Ж. Адамар и Ш. Ж. Ла Балле Пуссен получили асимптотич. закон распределения п. ч., доказав, что
Ж. Адамар и Ш. Ж. Ла Балле Пуссен получили асимптотич. закон распределения п. ч., доказав, что  не имеет нулей при
не имеет нулей при  . Для величины
. Для величины  доказаны так наз.
доказаны так наз. -теоремы: существуют такие две последовательности
-теоремы: существуют такие две последовательности  что
что

б) Другой проблемой теории распределения п. ч. является проблема оценки разности соседних п. ч., то есть числа 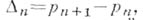 где
где  есть ге-е простое число. Здесь также первый общий результат принадлежит П. Л. Чебышеву, доказавшему, что между Nи 2N,
есть ге-е простое число. Здесь также первый общий результат принадлежит П. Л. Чебышеву, доказавшему, что между Nи 2N,  лежит п. ч. (Бертрана постулат). Оценка
лежит п. ч. (Бертрана постулат). Оценка  тесно связана с функцией
тесно связана с функцией  - числом нулей
- числом нулей  в прямоугольнике
в прямоугольнике  Функция
Функция  в свою очередь, тесно связана с функцией
в свою очередь, тесно связана с функцией  Существуют гипотезы:
Существуют гипотезы: 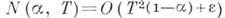 ( плот-ностная гипотеза).и
( плот-ностная гипотеза).и  ( Линделёфа гипотеза),
( Линделёфа гипотеза),  - произвольно мало. Из гипотезы Рима-на о нулях
- произвольно мало. Из гипотезы Рима-на о нулях  следует гипотеза Линделёфа, из гипотезы Линделёфа - плотностная гипотеза, из к-рой следует, что
следует гипотеза Линделёфа, из гипотезы Линделёфа - плотностная гипотеза, из к-рой следует, что  Доказано, что
Доказано, что  где
где
в)  Вопрос о распределении п. ч. в арифметич. прогрессиях
Вопрос о распределении п. ч. в арифметич. прогрессиях  приводит к вопросу о нулях специальных дзета-функций, так наз. L-рядов Дирихле, к-рые имеют вид:
приводит к вопросу о нулях специальных дзета-функций, так наз. L-рядов Дирихле, к-рые имеют вид:

 - коэффициенты, зависящие от пи от разности прогрессий
- коэффициенты, зависящие от пи от разности прогрессий 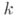 (характеры Дирихле по mod k).
(характеры Дирихле по mod k).
Проблемы распределения нулей L- рядов Дирихле и распределения п. ч. в арифметич. прогрессиях имеют свои специфич. особенности. Одно из самых крупных достижений в этом вопросе - следующее (К. Зигель; К. Siegel, 1935): пусть  - число п. ч., не превосходящих
- число п. ч., не превосходящих  в прогрессии
в прогрессии 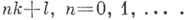 Тогда
Тогда

где  - Эйлера функция и
- Эйлера функция и  - произвольные фиксированные числа. Сведения о распределении п. ч. в арифметич. прогрессиях существенно используются при решении аддитивных задач с п. ч. См. также Распределение простых чисел.
- произвольные фиксированные числа. Сведения о распределении п. ч. в арифметич. прогрессиях существенно используются при решении аддитивных задач с п. ч. См. также Распределение простых чисел.
Аддитивные проблемы. К аддитивным задачам А. т. ч. относятся проблемы, связанные с уравнениями в целых числах специального вида. Основными вопросами в этой проблематике являются следующие: доказать разрешимость заданного уравнения, найти асимптотич. формулу для числа решений заданного уравнения. Второй вопрос значительно труднее, и положительный ответ на него в нек-ром смысле дает ответ на первый вопрос. Классич. примерами аддитивных задач являются Варинга проблемы, Гольдбаха проблема, Харди - Литлвуда проблема.
Проблема Варинга (1770) формулируется так: пусть  - число решений в целых положительных числах
- число решений в целых положительных числах  уравнения
уравнения

где  - целое число. Доказать, что существует такое число
- целое число. Доказать, что существует такое число  (k0 зависит только от п), что
(k0 зависит только от п), что  при
при  Другими словами, доказать, что любое число
Другими словами, доказать, что любое число  может быть представлено суммой
может быть представлено суммой 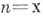 степеней целых положительных чисел, причем число слагаемых в этом представлении зависит только от п. При n=2 задача была решена Ж. Лагранжем (J. Lagrange, 1770), к-рый доказал, что каждое целое положительное число есть сумма четырех квадратов целых чисел. Первое общее решение проблемы Варинга дано Д. Гильбертом (D. Hilbert) в 1909. Позднее, в 1924 Г. X. Харди (G. H. Hardy) и Дж. Литлвуд (J. Little-wood), применив свой круговой метод, доказали, что для
степеней целых положительных чисел, причем число слагаемых в этом представлении зависит только от п. При n=2 задача была решена Ж. Лагранжем (J. Lagrange, 1770), к-рый доказал, что каждое целое положительное число есть сумма четырех квадратов целых чисел. Первое общее решение проблемы Варинга дано Д. Гильбертом (D. Hilbert) в 1909. Позднее, в 1924 Г. X. Харди (G. H. Hardy) и Дж. Литлвуд (J. Little-wood), применив свой круговой метод, доказали, что для  при
при  имеет место асимптотич. формула вида:
имеет место асимптотич. формула вида:

где  с - абсолютная константа. А поскольку существует бесконечно много таких чисел N, к-рые для k = n не являются суммой n-x степеней, т. е.
с - абсолютная константа. А поскольку существует бесконечно много таких чисел N, к-рые для k = n не являются суммой n-x степеней, т. е.  то возникла проблема установления истинного порядка величины kв зависимости от п, при к-ром разрешимо уравнение (1) п справедлива формула (2). Самые сильные результаты в этой проблеме принадлежат И. М. Виноградову, к-рый в 1934 доказал, что
то возникла проблема установления истинного порядка величины kв зависимости от п, при к-ром разрешимо уравнение (1) п справедлива формула (2). Самые сильные результаты в этой проблеме принадлежат И. М. Виноградову, к-рый в 1934 доказал, что
а)  при
при  если
если 
б) формула (2) имеет место при 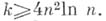
Другая классич. аддитивная проблема - проблема Гольдбаха - Эйлера (1742), состоит в следующем: пусть
 - число решений в простых числах
- число решений в простых числах  уравнения
уравнения  доказать, что при нечетном
доказать, что при нечетном  будет
будет 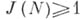 . В 1937 И. М. Виноградов доказал, что (асимптотич. формула для J(N)).
. В 1937 И. М. Виноградов доказал, что (асимптотич. формула для J(N)).

где  Отсюда, в частности, следует, что
Отсюда, в частности, следует, что  при
при 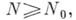 т. е. решение проблемы Гольдбаха - Эйлера для достаточно больших N.
т. е. решение проблемы Гольдбаха - Эйлера для достаточно больших N.
К аддитивным задачам относится проблема Харди - Литлвуда (1923); каждое  может быть представлено в виде
может быть представлено в виде  где
где 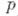 - простое число,
- простое число,  - целые положительные числа. В 1958 Ю. В. Линндк доказал, что если
- целые положительные числа. В 1958 Ю. В. Линндк доказал, что если  - число решений этого уравнения, то имеет место асимптотич. формула
- число решений этого уравнения, то имеет место асимптотич. формула
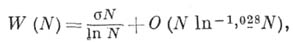
где  - абсолютная константа. Отсюда следует, что
- абсолютная константа. Отсюда следует, что  при
при  т. е. решение проблемы Харди - Литлвуда для достаточно больших N. Имеется много аддитивных проблем, к-рые еще не решены и имеют возраст сотен и даже тысяч лет. К ним, напр., относятся вопросы о бесконечности числа п. ч. близнецов, т. е. пар п. ч. ри qтаких, что
т. е. решение проблемы Харди - Литлвуда для достаточно больших N. Имеется много аддитивных проблем, к-рые еще не решены и имеют возраст сотен и даже тысяч лет. К ним, напр., относятся вопросы о бесконечности числа п. ч. близнецов, т. е. пар п. ч. ри qтаких, что  бинарная проблема Гольбаха - Эйлера, т. е., что каждое четное число
бинарная проблема Гольбаха - Эйлера, т. е., что каждое четное число  есть сумма двух п. ч., проблема существования бесконечного числа п. ч. в последовательности вида
есть сумма двух п. ч., проблема существования бесконечного числа п. ч. в последовательности вида  См. также Аддитивные проблемы.
См. также Аддитивные проблемы.
Поведение теоретико-числовых функций. В теории чисел имеется ряд классич. функций: 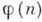 - число чисел, не превосходящих
- число чисел, не превосходящих  и взаимно простых с п(функция Эйлера),
и взаимно простых с п(функция Эйлера),  - число делителей числа п,
- число делителей числа п,  - Мёбиуса функция,
- Мёбиуса функция, - Манголъдта функция и др. Несмотря на то, что каждая из указанных функции ведет себя довольно "неправильно", средние значения этих функций уже поддаются изучению. Под средним значением функции
- Манголъдта функция и др. Несмотря на то, что каждая из указанных функции ведет себя довольно "неправильно", средние значения этих функций уже поддаются изучению. Под средним значением функции  понимают величину
понимают величину  Вопрос об оценке среднего значения функции
Вопрос об оценке среднего значения функции  эквивалентен вопросу о границе нулей дзета-функции Рпмана. Вопрос об асимптотике среднего значения функции
эквивалентен вопросу о границе нулей дзета-функции Рпмана. Вопрос об асимптотике среднего значения функции  эквивалентен вопросу об асимптотич. формуле для
эквивалентен вопросу об асимптотич. формуле для  , т. е. также вопросу о границе нулей дзета-функции Римана. Во всех этих задачах достигнуты те же результаты, что и в проблеме распределения п. ч. Особо стоит вопрос об асимптотике среднего значения
, т. е. также вопросу о границе нулей дзета-функции Римана. Во всех этих задачах достигнуты те же результаты, что и в проблеме распределения п. ч. Особо стоит вопрос об асимптотике среднего значения  или, несколько иначе, вопрос об асимптотич. формуле для суммы значений
или, несколько иначе, вопрос об асимптотич. формуле для суммы значений  . Пусть
. Пусть

Тогда  - число целых точек под гиперболой
- число целых точек под гиперболой 
 Таким образом, нахождение асимптотики
Таким образом, нахождение асимптотики  - это проблема нахождения асимптотики числа целых точек в расширяющихся областях. К этой проблематике относится задача о числе целых точек в круге, т. е. задача о числе
- это проблема нахождения асимптотики числа целых точек в расширяющихся областях. К этой проблематике относится задача о числе целых точек в круге, т. е. задача о числе

х, у - целые числа, п обобщения этих задач на произвольные области как на плоскости, так и в пространстве, П. Дирихле (1849) доказал, что
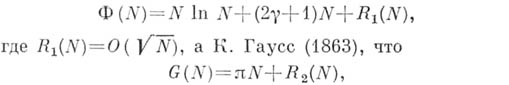
где  Задачи нахождения наилучших возможных оценок величин
Задачи нахождения наилучших возможных оценок величин  стали наз. соответственно делителей проблемой и круга проблемой. Г. Ф. Вороной (1903) получил
стали наз. соответственно делителей проблемой и круга проблемой. Г. Ф. Вороной (1903) получил

а В. Серпиньский ( ) -
) -

Кроме того, доказаны  -теоремы, а именно, что
-теоремы, а именно, что

В настоящее время (1976) получены оценки  и
и  несколько лучше, чем у Г. Ф. Вороного и В. Сер-пиньского.
несколько лучше, чем у Г. Ф. Вороного и В. Сер-пиньского.
Родственной рассмотренным задачам является задача об асимптотике суммы дробных долей различного вида функций или эквивалентная ей задача - вопрос о распределении дробных долей различного вида функций. Обозначим через 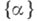 дробную часть числа
дробную часть числа  Тогда если
Тогда если  - вещественная функция, то возникает вопрос об асимптотике следующих двух функций:
- вещественная функция, то возникает вопрос об асимптотике следующих двух функций:

Если для любого 

то говорят, что дробные доли функции  распределены равномерно. Равномерность распределения дробных долей функции
распределены равномерно. Равномерность распределения дробных долей функции  может быть выражена и в терминах асимптотики для
может быть выражена и в терминах асимптотики для  . Первые результаты о равномерном распределении дробных долей многочленов, критерии равномерного распределения были найдены Г. Вейлем (Н. Weyl, 1916). Наиболее точные результаты в этих вопросах получены И. <М. <Виноградовым. Им же найдены асимптотич. формулы для
. Первые результаты о равномерном распределении дробных долей многочленов, критерии равномерного распределения были найдены Г. Вейлем (Н. Weyl, 1916). Наиболее точные результаты в этих вопросах получены И. <М. <Виноградовым. Им же найдены асимптотич. формулы для  и
и  п для тех случаев, когда ппробегает часть множества целых чисел, не превосходящих N, в частности множество п. ч. Относительно мало известно о распределении дробных долей функций, растущих быстрее многочленов. Напр., ничего не известно о распределении дробных долей функции
п для тех случаев, когда ппробегает часть множества целых чисел, не превосходящих N, в частности множество п. ч. Относительно мало известно о распределении дробных долей функций, растущих быстрее многочленов. Напр., ничего не известно о распределении дробных долей функции  .
.
Алгебраические и трансцендентные числа. К теории алгебраических и трансцендентных чисел относятся вопросы, связанные с арифметич. природой тех или иных чисел или классов чисел. Рассмотрим многочлены с целыми коэффициентами и старшим коэффициентом 1; если  является корнем такого многочлена степени пи не является корнем многочлена меньшей степени, то оно наз. алгебраическим числом степени п;при n = 1 число
является корнем такого многочлена степени пи не является корнем многочлена меньшей степени, то оно наз. алгебраическим числом степени п;при n = 1 число  наз. рациональным. Если же
наз. рациональным. Если же  не является алгебраическим, то оно наз. трансцендентным числом. Алгебрапч. чисел "много меньше", чем трансцендентных, "почти любое" число - трансцендентное, однако вопросы об алгебраичности или трансцендентности конкретных чисел очень трудны. Основной "характеристикой" алгебраич. числа является тот факт, что они "плохо" приближаются рациональными числами. Это утверждение (Лиувилля теорема,1844) формулируется так: если
не является алгебраическим, то оно наз. трансцендентным числом. Алгебрапч. чисел "много меньше", чем трансцендентных, "почти любое" число - трансцендентное, однако вопросы об алгебраичности или трансцендентности конкретных чисел очень трудны. Основной "характеристикой" алгебраич. числа является тот факт, что они "плохо" приближаются рациональными числами. Это утверждение (Лиувилля теорема,1844) формулируется так: если  - алгебраич. число степени п, то
- алгебраич. число степени п, то

где  - константа, зависящая только от a, а ри q - произвольные целые числа. Следующий принципиальный шаг в этом вопросе сделал А. Туэ (A. Thue, 1909), идеи к-рого оказали большое влияние на всю теорию трансцендентных чисел. Он доказал, что
- константа, зависящая только от a, а ри q - произвольные целые числа. Следующий принципиальный шаг в этом вопросе сделал А. Туэ (A. Thue, 1909), идеи к-рого оказали большое влияние на всю теорию трансцендентных чисел. Он доказал, что  Далее величина хуменьшалась многими учеными, и в 1955 К. Ф. Рот (К. F. Roth) доказал, что
Далее величина хуменьшалась многими учеными, и в 1955 К. Ф. Рот (К. F. Roth) доказал, что  (известно, что
(известно, что  ). Недостатком этих теорем (исключая теорему Лиувилля) является то, что все они не эффективны, т. е. по
). Недостатком этих теорем (исключая теорему Лиувилля) является то, что все они не эффективны, т. е. по  и е нельзя вычислять с.
и е нельзя вычислять с.
Задачи о приближениях связаны с определенным классом задач из теории неопределенных уравнений. Так, А. Туэ из своей теоремы о приближении получил конечность числа целочисленных решений уравнения 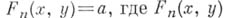 - форма с целыми коэффициентами степени
- форма с целыми коэффициентами степени  , а - целое число, отличное от нуля (эта теорема также не эффективна, т. е. нельзя указать границы для решений уравнения).
, а - целое число, отличное от нуля (эта теорема также не эффективна, т. е. нельзя указать границы для решений уравнения).
Другое направление этой теории - доказательство трансцендентности чисел. Первые результаты здесь были получены в конце 19 в. Ш. Эрмит (Ch. Hermite, 1873) доказал трансцендентность числа е;Ф. Линдеман (F. Lindemann, 1882) - трансцендентность числа л, и тем самым была отрицательно решена проблема о квадратуре круга. А. О. Гельфонд и Т. Шнейдер (Т. Schneider) в 1934 доказали теорему о том, что  является трансцендентным числом, если
является трансцендентным числом, если  - алгебраич. число
- алгебраич. число  - алгебраич. число степени
- алгебраич. число степени  (седьмая проблема Гильберта). А. Бейкером (A. Baker) начиная с 1967 был получен ряд эффективных теорем об оценке линейных форм от логарифмов алгебраич. чисел. Следствием этих теорем явилось эффективное доказательство теоремы Туэ о числе представлений целого числа формой. Существует много вопросов в теории трансцендентных чисел, к-рые еще ждут своего решения. К ним относятся вопрос о трансцендентности константы Эйлера
(седьмая проблема Гильберта). А. Бейкером (A. Baker) начиная с 1967 был получен ряд эффективных теорем об оценке линейных форм от логарифмов алгебраич. чисел. Следствием этих теорем явилось эффективное доказательство теоремы Туэ о числе представлений целого числа формой. Существует много вопросов в теории трансцендентных чисел, к-рые еще ждут своего решения. К ним относятся вопрос о трансцендентности константы Эйлера

вопрос об алгебраич. зависимости чисел еи p и др. О некоторых методах в аналитической теории чисел.
а) Метод комплексного интегрирования. Он порожден методом производящих функций Эйлера, к-рым часто решаются задачи элементарной математики. Основой служит следующая формула (разрывный множитель):

где интеграл берется по прямой  Так, при
Так, при  имеем
имеем

и при  получаем
получаем
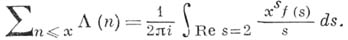
Слева стоит Чебышева функция, асимптотика для к-рой эквивалентна проблеме о п. ч. Правая же часть, после выделения главного члена, будет тем меньше, чем левее удастся перенести контур интегрирования. См. также Комплексного интегрирования метод.
б) Круговой метод (Харди - Литлвуда - Рамануджана). Он применяется в основном в аддитивных задачах. Рассмотрим схему применения и существо кругового метода в форме тригонометрич. сумм Виноградова на тернарной проблеме Гольдбаха - Эйлера. Пусть 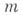 - целое число. Тогда имеем (разрывный множитель):
- целое число. Тогда имеем (разрывный множитель):

Поэтому

 - число решений в п. ч. уравнения
- число решений в п. ч. уравнения 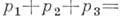
 . Далее, интервал интегрирования
. Далее, интервал интегрирования  разбивается на две части - основной интервал и дополнительный: к основному интервалу относят все интервалы вида
разбивается на две части - основной интервал и дополнительный: к основному интервалу относят все интервалы вида

где  к дополнительному интервалу отнесем все остальные. Основные интервалы не пересекаются. Кроме того, для
к дополнительному интервалу отнесем все остальные. Основные интервалы не пересекаются. Кроме того, для 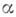 из основного интервала, сумма
из основного интервала, сумма  "близка" к рациональной сумме
"близка" к рациональной сумме  . Но при "малых"
. Но при "малых"  , известен закон распределения п. ч. в прогрессиях с разностью
, известен закон распределения п. ч. в прогрессиях с разностью  (напр., теорема Зигеля), т. е. известна асимптотика сумм
(напр., теорема Зигеля), т. е. известна асимптотика сумм  Так выделяется главный член проблемы, и в этом состоит идея кругового метода. Если теперь нетривиально оценить
Так выделяется главный член проблемы, и в этом состоит идея кругового метода. Если теперь нетривиально оценить  на дополнительных интервалах (см. Виноградова метод), то получится асимптотич. формула в проблеме Гольдбаха - Эйлера. См. также Круговой метод.
на дополнительных интервалах (см. Виноградова метод), то получится асимптотич. формула в проблеме Гольдбаха - Эйлера. См. также Круговой метод.
в) Метод тригонометрических сумм. Большинство задач А. т. ч. может быть сформулировано в терминах тригонометрич. сумм - конечных сумм вида
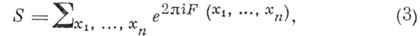
где  - действительная функция, а
- действительная функция, а 
 пробегают множество целых чисел в количестве Р. Таким образом, центр тяжести многих проблем переносится на задачу изучения таких сумм, в частности на задачу получения возможно более точной оценки модуля таких сумм. Тривиальной оценкой суммы (3) будет Р. Ставится задача получить оценку типа
пробегают множество целых чисел в количестве Р. Таким образом, центр тяжести многих проблем переносится на задачу изучения таких сумм, в частности на задачу получения возможно более точной оценки модуля таких сумм. Тривиальной оценкой суммы (3) будет Р. Ставится задача получить оценку типа

где  наз. понижающим множителем. Первые нетривиальные оценки тригонометрич. сумм, когда
наз. понижающим множителем. Первые нетривиальные оценки тригонометрич. сумм, когда 
 - многочлен, а
- многочлен, а  получил Г. Вейль (1919), к-рый одновременно доказал критерий равнораспределенности дробных долей функции в терминах тригонометрич. сумм. Создателем метода тригонометрич. сумм является И. М. Виноградов, к-рый, используя глубокие арифметич. свойства рассматриваемых сумм, получил исключительно сильные оценки модуля широкого класса таких сумм. Это позволило ему получить фундаментальные близкие к предельно возможным результаты в целом ряде вопросов теории чисел (проблема Варинга, Гильберта- Камке проблема, Вейля суммы). Другим следствием метода Виноградова (1937) было решение ряда аддитивных проблем с п. ч. и, в частности, решение проблемы Гольдбаха - Эйлера. Основной идеей метода Виноградова является идея "сглаживания" (возведение в степень тригонометрич. суммы и сведение оценки к теореме о среднем при оценках сумм Вейля; введение двойных тригонометрич. сумм при оценках сумм с п. ч.). См. также Тригонометрических сумм метод.
получил Г. Вейль (1919), к-рый одновременно доказал критерий равнораспределенности дробных долей функции в терминах тригонометрич. сумм. Создателем метода тригонометрич. сумм является И. М. Виноградов, к-рый, используя глубокие арифметич. свойства рассматриваемых сумм, получил исключительно сильные оценки модуля широкого класса таких сумм. Это позволило ему получить фундаментальные близкие к предельно возможным результаты в целом ряде вопросов теории чисел (проблема Варинга, Гильберта- Камке проблема, Вейля суммы). Другим следствием метода Виноградова (1937) было решение ряда аддитивных проблем с п. ч. и, в частности, решение проблемы Гольдбаха - Эйлера. Основной идеей метода Виноградова является идея "сглаживания" (возведение в степень тригонометрич. суммы и сведение оценки к теореме о среднем при оценках сумм Вейля; введение двойных тригонометрич. сумм при оценках сумм с п. ч.). См. также Тригонометрических сумм метод.
г) Дисперсионный метод и метод большого решета. В 1958- 60 Ю. В. Линником был создан дисперсионный метод для решения целого ряда аддитивных задач теории чисел. Им были решены проблема Харди - Литлвуда, Титчмарша проблема делителей, аддитивная проблема делителей. Основным понятием метода является дисперсия для числа решений уравнения при предполагаемой асимптотике для числа решений нек-рого вспомогательного уравнения, связанного с основным (см. также Дисперсионный метод). В последнее время получены глубокие результаты при помощи метода большого решета Ю. В. Линника, к-рый был создан им в 1940 при решении проблемы о наименьшем квадратичном невычете.
д) Методы в теории алгебраических и трансцендентных чисел. При доказательстве теоремы о приближении алгебранч. числа рациональной дробью, А. Туэ (см. Туэ метод).строит многочлен

с целыми коэффициентами, где  и
и  - тоже многочлены. Допуская, что
- тоже многочлены. Допуская, что  "хорошо" приближаются дробями
"хорошо" приближаются дробями  и
и  с достаточно большим
с достаточно большим  и
и 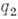 , полагая
, полагая 
 и доказывая, что
и доказывая, что  при
при 
 не обращается в нуль, получают противоречие. При доказательстве трансцендентности чисел А. О. Гельфонд строит функцию
не обращается в нуль, получают противоречие. При доказательстве трансцендентности чисел А. О. Гельфонд строит функцию

В предположении, что  - алгебраич. число, при помощи принципа ящиков Дирихле целые не равные нулю числа
- алгебраич. число, при помощи принципа ящиков Дирихле целые не равные нулю числа  выбираются так, что
выбираются так, что  и "много" ее производных имеют "много" нулей. "Большое" количество нулей позволяет получить "хорошие" оценки сверху для "большого" числа производных и точек, а отсюда, при помощи оценок снизу, получаемых из теоремы Лиувилля, следует, что
и "много" ее производных имеют "много" нулей. "Большое" количество нулей позволяет получить "хорошие" оценки сверху для "большого" числа производных и точек, а отсюда, при помощи оценок снизу, получаемых из теоремы Лиувилля, следует, что 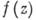 и "много" ее производных имеют больше нулей, чем вначале. Повторение этого процесса приводит к тому, что либо
и "много" ее производных имеют больше нулей, чем вначале. Повторение этого процесса приводит к тому, что либо  - рациональное число, либо
- рациональное число, либо  равны нулю, что противоречит их выбору. См. также Алгебраическое число, Трансцендентное число. Лит.:[1] Виноградов И. М., Избр. тр., М., 1952; [2]его же, Основы теории чисел, 7 изд., М., 1965; [3] его же, Метод тригонометрических сумм в теории чисел, М., 1971; [4] Гельфонд А. О., Трансцендентные и алгебраические числа, М., 1952; [5] Делове Б. Н., Петербургская школа теории чисел, М.-Л., 1947; [6] Карацуба А. А., Основы аналитической теории чисел, М., 1975; [7] Линвик Ю. В., Дисперсионный метод в бинарных аддитивных задачах, Л., 1961; [8] Чудаков Н. Г., Введение в теорию L-функций Дирихле, М.-Л., 1947; [9] Прахар К., Распределение простых чисел, пер. с нем., М., 1967; [10] Дэвенпорт Г., Мультипликативная теория чисел, пер. с англ., М., 1971; [11] Титчмарш Е., Теория дзета-функции Римана, пер. с англ., М., 1953; [12] Xуа Ло-ген, Метод тригонометрических сумм и его применения в теории чисел, пер. с нем., М., 1964; [13] Ваkеr A., "Mathematika", 1967, v. 14, №1(27), p. 102-07; [14] Виноградов А. И., "Изв. АН СССР. Серия матем.", 1965, т. 29, в. 4, с. 903-34; [15] Воmbiеri E., "Mathematiba", 1965, v. 12, №24, p. 201-25. А. А. Карацуба.
равны нулю, что противоречит их выбору. См. также Алгебраическое число, Трансцендентное число. Лит.:[1] Виноградов И. М., Избр. тр., М., 1952; [2]его же, Основы теории чисел, 7 изд., М., 1965; [3] его же, Метод тригонометрических сумм в теории чисел, М., 1971; [4] Гельфонд А. О., Трансцендентные и алгебраические числа, М., 1952; [5] Делове Б. Н., Петербургская школа теории чисел, М.-Л., 1947; [6] Карацуба А. А., Основы аналитической теории чисел, М., 1975; [7] Линвик Ю. В., Дисперсионный метод в бинарных аддитивных задачах, Л., 1961; [8] Чудаков Н. Г., Введение в теорию L-функций Дирихле, М.-Л., 1947; [9] Прахар К., Распределение простых чисел, пер. с нем., М., 1967; [10] Дэвенпорт Г., Мультипликативная теория чисел, пер. с англ., М., 1971; [11] Титчмарш Е., Теория дзета-функции Римана, пер. с англ., М., 1953; [12] Xуа Ло-ген, Метод тригонометрических сумм и его применения в теории чисел, пер. с нем., М., 1964; [13] Ваkеr A., "Mathematika", 1967, v. 14, №1(27), p. 102-07; [14] Виноградов А. И., "Изв. АН СССР. Серия матем.", 1965, т. 29, в. 4, с. 903-34; [15] Воmbiеri E., "Mathematiba", 1965, v. 12, №24, p. 201-25. А. А. Карацуба.

 при
при 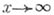 . Следующий шаг в этом вопросе был сделан П. Л. Чебышевым (1850). Он доказал, что:
. Следующий шаг в этом вопросе был сделан П. Л. Чебышевым (1850). Он доказал, что: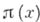 выполняются неравенства
выполняются неравенства 

 то этот предел равен 1.
то этот предел равен 1.


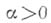 - абсолютная постоянная (см. Балле Пуссена теорема). При решении этой проблемы были использованы методы теории функций комплексного переменного. С проблемой оценки
- абсолютная постоянная (см. Балле Пуссена теорема). При решении этой проблемы были использованы методы теории функций комплексного переменного. С проблемой оценки  тесно связана проблема поведения нек-рой функции комплексного переменного, к-рую впервые (1859) изучал Б. Риман (В. Riemann), и к-рая теперь наз. Рпмана дзета-функцией. Эта функция задается равенством
тесно связана проблема поведения нек-рой функции комплексного переменного, к-рую впервые (1859) изучал Б. Риман (В. Riemann), и к-рая теперь наз. Рпмана дзета-функцией. Эта функция задается равенством 
 с п. ч.:
с п. ч.:
 , заданную рядом при
, заданную рядом при  , можно аналитически продолжить на всю плоскость комплексного переменного; тогда получится функция, к-рая будет аналитической на всей плоскости комплексного переменного за исклю-.ченпем точки
, можно аналитически продолжить на всю плоскость комплексного переменного; тогда получится функция, к-рая будет аналитической на всей плоскости комплексного переменного за исклю-.ченпем точки  , где она имеет простой полюс с вычетом, равным 1. Проблема оценки остатка
, где она имеет простой полюс с вычетом, равным 1. Проблема оценки остатка  в асимптотич. формуле распределения п. ч. тесно связана с проблемой распределения нулей
в асимптотич. формуле распределения п. ч. тесно связана с проблемой распределения нулей  в "критической" полосе
в "критической" полосе 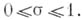 Б. Риманом была высказана гипотеза, что все нули
Б. Риманом была высказана гипотеза, что все нули  в критич. полосе лежат на прямой
в критич. полосе лежат на прямой 
 Из этой гипотезы следует, что
Из этой гипотезы следует, что  Наоборот, из соотношения
Наоборот, из соотношения  - произвольно мало, следует справедливость Римана гипотезы о нулях
- произвольно мало, следует справедливость Римана гипотезы о нулях  Ж. Адамар и Ш. Ж. Ла Балле Пуссен получили асимптотич. закон распределения п. ч., доказав, что
Ж. Адамар и Ш. Ж. Ла Балле Пуссен получили асимптотич. закон распределения п. ч., доказав, что  не имеет нулей при
не имеет нулей при  . Для величины
. Для величины  доказаны так наз.
доказаны так наз. -теоремы: существуют такие две последовательности
-теоремы: существуют такие две последовательности  что
что 
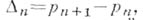 где
где  есть ге-е простое число. Здесь также первый общий результат принадлежит П. Л. Чебышеву, доказавшему, что между Nи 2N,
есть ге-е простое число. Здесь также первый общий результат принадлежит П. Л. Чебышеву, доказавшему, что между Nи 2N,  лежит п. ч. (Бертрана постулат). Оценка
лежит п. ч. (Бертрана постулат). Оценка  тесно связана с функцией
тесно связана с функцией  - числом нулей
- числом нулей  в прямоугольнике
в прямоугольнике  Функция
Функция  в свою очередь, тесно связана с функцией
в свою очередь, тесно связана с функцией  Существуют гипотезы:
Существуют гипотезы: 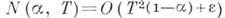 ( плот-ностная гипотеза).и
( плот-ностная гипотеза).и  ( Линделёфа гипотеза),
( Линделёфа гипотеза),  - произвольно мало. Из гипотезы Рима-на о нулях
- произвольно мало. Из гипотезы Рима-на о нулях  следует гипотеза Линделёфа, из гипотезы Линделёфа - плотностная гипотеза, из к-рой следует, что
следует гипотеза Линделёфа, из гипотезы Линделёфа - плотностная гипотеза, из к-рой следует, что  Доказано, что
Доказано, что  где
где  Вопрос о распределении п. ч. в арифметич. прогрессиях
Вопрос о распределении п. ч. в арифметич. прогрессиях  приводит к вопросу о нулях специальных дзета-функций, так наз. L-рядов Дирихле, к-рые имеют вид:
приводит к вопросу о нулях специальных дзета-функций, так наз. L-рядов Дирихле, к-рые имеют вид:
 - коэффициенты, зависящие от пи от разности прогрессий
- коэффициенты, зависящие от пи от разности прогрессий 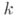 (характеры Дирихле по mod k).
(характеры Дирихле по mod k). - число п. ч., не превосходящих
- число п. ч., не превосходящих  в прогрессии
в прогрессии 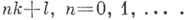 Тогда
Тогда 
 - Эйлера функция и
- Эйлера функция и  - произвольные фиксированные числа. Сведения о распределении п. ч. в арифметич. прогрессиях существенно используются при решении аддитивных задач с п. ч. См. также Распределение простых чисел.
- произвольные фиксированные числа. Сведения о распределении п. ч. в арифметич. прогрессиях существенно используются при решении аддитивных задач с п. ч. См. также Распределение простых чисел. - число решений в целых положительных числах
- число решений в целых положительных числах  уравнения
уравнения 
 - целое число. Доказать, что существует такое число
- целое число. Доказать, что существует такое число  (k0 зависит только от п), что
(k0 зависит только от п), что  при
при  Другими словами, доказать, что любое число
Другими словами, доказать, что любое число  может быть представлено суммой
может быть представлено суммой 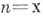 степеней целых положительных чисел, причем число слагаемых в этом представлении зависит только от п. При n=2 задача была решена Ж. Лагранжем (J. Lagrange, 1770), к-рый доказал, что каждое целое положительное число есть сумма четырех квадратов целых чисел. Первое общее решение проблемы Варинга дано Д. Гильбертом (D. Hilbert) в 1909. Позднее, в 1924 Г. X. Харди (G. H. Hardy) и Дж. Литлвуд (J. Little-wood), применив свой круговой метод, доказали, что для
степеней целых положительных чисел, причем число слагаемых в этом представлении зависит только от п. При n=2 задача была решена Ж. Лагранжем (J. Lagrange, 1770), к-рый доказал, что каждое целое положительное число есть сумма четырех квадратов целых чисел. Первое общее решение проблемы Варинга дано Д. Гильбертом (D. Hilbert) в 1909. Позднее, в 1924 Г. X. Харди (G. H. Hardy) и Дж. Литлвуд (J. Little-wood), применив свой круговой метод, доказали, что для  при
при  имеет место асимптотич. формула вида:
имеет место асимптотич. формула вида:
 с - абсолютная константа. А поскольку существует бесконечно много таких чисел N, к-рые для k = n не являются суммой n-x степеней, т. е.
с - абсолютная константа. А поскольку существует бесконечно много таких чисел N, к-рые для k = n не являются суммой n-x степеней, т. е.  то возникла проблема установления истинного порядка величины kв зависимости от п, при к-ром разрешимо уравнение (1) п справедлива формула (2). Самые сильные результаты в этой проблеме принадлежат И. М. Виноградову, к-рый в 1934 доказал, что
то возникла проблема установления истинного порядка величины kв зависимости от п, при к-ром разрешимо уравнение (1) п справедлива формула (2). Самые сильные результаты в этой проблеме принадлежат И. М. Виноградову, к-рый в 1934 доказал, что  при
при  если
если 
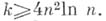
 - число решений в простых числах
- число решений в простых числах  уравнения
уравнения  доказать, что при нечетном
доказать, что при нечетном  будет
будет 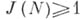 . В 1937 И. М. Виноградов доказал, что (асимптотич. формула для J(N)).
. В 1937 И. М. Виноградов доказал, что (асимптотич. формула для J(N)).
 Отсюда, в частности, следует, что
Отсюда, в частности, следует, что  при
при 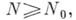 т. е. решение проблемы Гольдбаха - Эйлера для достаточно больших N.
т. е. решение проблемы Гольдбаха - Эйлера для достаточно больших N. может быть представлено в виде
может быть представлено в виде  где
где 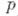 - простое число,
- простое число,  - целые положительные числа. В 1958 Ю. В. Линндк доказал, что если
- целые положительные числа. В 1958 Ю. В. Линндк доказал, что если  - число решений этого уравнения, то имеет место асимптотич. формула
- число решений этого уравнения, то имеет место асимптотич. формула 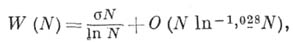
 - абсолютная константа. Отсюда следует, что
- абсолютная константа. Отсюда следует, что  при
при  т. е. решение проблемы Харди - Литлвуда для достаточно больших N. Имеется много аддитивных проблем, к-рые еще не решены и имеют возраст сотен и даже тысяч лет. К ним, напр., относятся вопросы о бесконечности числа п. ч. близнецов, т. е. пар п. ч. ри qтаких, что
т. е. решение проблемы Харди - Литлвуда для достаточно больших N. Имеется много аддитивных проблем, к-рые еще не решены и имеют возраст сотен и даже тысяч лет. К ним, напр., относятся вопросы о бесконечности числа п. ч. близнецов, т. е. пар п. ч. ри qтаких, что  бинарная проблема Гольбаха - Эйлера, т. е., что каждое четное число
бинарная проблема Гольбаха - Эйлера, т. е., что каждое четное число  есть сумма двух п. ч., проблема существования бесконечного числа п. ч. в последовательности вида
есть сумма двух п. ч., проблема существования бесконечного числа п. ч. в последовательности вида  См. также Аддитивные проблемы.
См. также Аддитивные проблемы.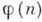 - число чисел, не превосходящих
- число чисел, не превосходящих  и взаимно простых с п(функция Эйлера),
и взаимно простых с п(функция Эйлера),  - число делителей числа п,
- число делителей числа п,  - Мёбиуса функция,
- Мёбиуса функция, - Манголъдта функция и др. Несмотря на то, что каждая из указанных функции ведет себя довольно "неправильно", средние значения этих функций уже поддаются изучению. Под средним значением функции
- Манголъдта функция и др. Несмотря на то, что каждая из указанных функции ведет себя довольно "неправильно", средние значения этих функций уже поддаются изучению. Под средним значением функции  понимают величину
понимают величину  Вопрос об оценке среднего значения функции
Вопрос об оценке среднего значения функции  эквивалентен вопросу о границе нулей дзета-функции Рпмана. Вопрос об асимптотике среднего значения функции
эквивалентен вопросу о границе нулей дзета-функции Рпмана. Вопрос об асимптотике среднего значения функции  эквивалентен вопросу об асимптотич. формуле для
эквивалентен вопросу об асимптотич. формуле для  , т. е. также вопросу о границе нулей дзета-функции Римана. Во всех этих задачах достигнуты те же результаты, что и в проблеме распределения п. ч. Особо стоит вопрос об асимптотике среднего значения
, т. е. также вопросу о границе нулей дзета-функции Римана. Во всех этих задачах достигнуты те же результаты, что и в проблеме распределения п. ч. Особо стоит вопрос об асимптотике среднего значения  или, несколько иначе, вопрос об асимптотич. формуле для суммы значений
или, несколько иначе, вопрос об асимптотич. формуле для суммы значений  . Пусть
. Пусть 
 - число целых точек под гиперболой
- число целых точек под гиперболой 
 Таким образом, нахождение асимптотики
Таким образом, нахождение асимптотики  - это проблема нахождения асимптотики числа целых точек в расширяющихся областях. К этой проблематике относится задача о числе целых точек в круге, т. е. задача о числе
- это проблема нахождения асимптотики числа целых точек в расширяющихся областях. К этой проблематике относится задача о числе целых точек в круге, т. е. задача о числе
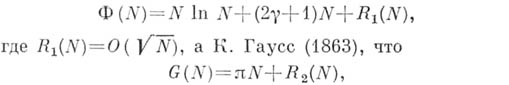
 Задачи нахождения наилучших возможных оценок величин
Задачи нахождения наилучших возможных оценок величин  стали наз. соответственно делителей проблемой и круга проблемой. Г. Ф. Вороной (1903) получил
стали наз. соответственно делителей проблемой и круга проблемой. Г. Ф. Вороной (1903) получил 
 ) -
) -
 -теоремы, а именно, что
-теоремы, а именно, что 
 и
и  несколько лучше, чем у Г. Ф. Вороного и В. Сер-пиньского.
несколько лучше, чем у Г. Ф. Вороного и В. Сер-пиньского.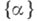 дробную часть числа
дробную часть числа  Тогда если
Тогда если  - вещественная функция, то возникает вопрос об асимптотике следующих двух функций:
- вещественная функция, то возникает вопрос об асимптотике следующих двух функций:


 распределены равномерно. Равномерность распределения дробных долей функции
распределены равномерно. Равномерность распределения дробных долей функции  может быть выражена и в терминах асимптотики для
может быть выражена и в терминах асимптотики для  . Первые результаты о равномерном распределении дробных долей многочленов, критерии равномерного распределения были найдены Г. Вейлем (Н. Weyl, 1916). Наиболее точные результаты в этих вопросах получены И. <М. <Виноградовым. Им же найдены асимптотич. формулы для
. Первые результаты о равномерном распределении дробных долей многочленов, критерии равномерного распределения были найдены Г. Вейлем (Н. Weyl, 1916). Наиболее точные результаты в этих вопросах получены И. <М. <Виноградовым. Им же найдены асимптотич. формулы для  и
и  п для тех случаев, когда ппробегает часть множества целых чисел, не превосходящих N, в частности множество п. ч. Относительно мало известно о распределении дробных долей функций, растущих быстрее многочленов. Напр., ничего не известно о распределении дробных долей функции
п для тех случаев, когда ппробегает часть множества целых чисел, не превосходящих N, в частности множество п. ч. Относительно мало известно о распределении дробных долей функций, растущих быстрее многочленов. Напр., ничего не известно о распределении дробных долей функции  .
. является корнем такого многочлена степени пи не является корнем многочлена меньшей степени, то оно наз. алгебраическим числом степени п;при n = 1 число
является корнем такого многочлена степени пи не является корнем многочлена меньшей степени, то оно наз. алгебраическим числом степени п;при n = 1 число  наз. рациональным. Если же
наз. рациональным. Если же  не является алгебраическим, то оно наз. трансцендентным числом. Алгебрапч. чисел "много меньше", чем трансцендентных, "почти любое" число - трансцендентное, однако вопросы об алгебраичности или трансцендентности конкретных чисел очень трудны. Основной "характеристикой" алгебраич. числа является тот факт, что они "плохо" приближаются рациональными числами. Это утверждение (Лиувилля теорема,1844) формулируется так: если
не является алгебраическим, то оно наз. трансцендентным числом. Алгебрапч. чисел "много меньше", чем трансцендентных, "почти любое" число - трансцендентное, однако вопросы об алгебраичности или трансцендентности конкретных чисел очень трудны. Основной "характеристикой" алгебраич. числа является тот факт, что они "плохо" приближаются рациональными числами. Это утверждение (Лиувилля теорема,1844) формулируется так: если  - алгебраич. число степени п, то
- алгебраич. число степени п, то
 - константа, зависящая только от a, а ри q - произвольные целые числа. Следующий принципиальный шаг в этом вопросе сделал А. Туэ (A. Thue, 1909), идеи к-рого оказали большое влияние на всю теорию трансцендентных чисел. Он доказал, что
- константа, зависящая только от a, а ри q - произвольные целые числа. Следующий принципиальный шаг в этом вопросе сделал А. Туэ (A. Thue, 1909), идеи к-рого оказали большое влияние на всю теорию трансцендентных чисел. Он доказал, что  Далее величина хуменьшалась многими учеными, и в 1955 К. Ф. Рот (К. F. Roth) доказал, что
Далее величина хуменьшалась многими учеными, и в 1955 К. Ф. Рот (К. F. Roth) доказал, что  (известно, что
(известно, что  ). Недостатком этих теорем (исключая теорему Лиувилля) является то, что все они не эффективны, т. е. по
). Недостатком этих теорем (исключая теорему Лиувилля) является то, что все они не эффективны, т. е. по  и е нельзя вычислять с.
и е нельзя вычислять с.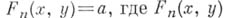 - форма с целыми коэффициентами степени
- форма с целыми коэффициентами степени  , а - целое число, отличное от нуля (эта теорема также не эффективна, т. е. нельзя указать границы для решений уравнения).
, а - целое число, отличное от нуля (эта теорема также не эффективна, т. е. нельзя указать границы для решений уравнения). является трансцендентным числом, если
является трансцендентным числом, если  - алгебраич. число
- алгебраич. число  - алгебраич. число степени
- алгебраич. число степени  (седьмая проблема Гильберта). А. Бейкером (A. Baker) начиная с 1967 был получен ряд эффективных теорем об оценке линейных форм от логарифмов алгебраич. чисел. Следствием этих теорем явилось эффективное доказательство теоремы Туэ о числе представлений целого числа формой. Существует много вопросов в теории трансцендентных чисел, к-рые еще ждут своего решения. К ним относятся вопрос о трансцендентности константы Эйлера
(седьмая проблема Гильберта). А. Бейкером (A. Baker) начиная с 1967 был получен ряд эффективных теорем об оценке линейных форм от логарифмов алгебраич. чисел. Следствием этих теорем явилось эффективное доказательство теоремы Туэ о числе представлений целого числа формой. Существует много вопросов в теории трансцендентных чисел, к-рые еще ждут своего решения. К ним относятся вопрос о трансцендентности константы Эйлера 

 Так, при
Так, при  имеем
имеем 
 получаем
получаем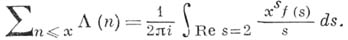
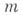 - целое число. Тогда имеем (разрывный множитель):
- целое число. Тогда имеем (разрывный множитель):

 - число решений в п. ч. уравнения
- число решений в п. ч. уравнения 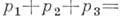
 . Далее, интервал интегрирования
. Далее, интервал интегрирования  разбивается на две части - основной интервал и дополнительный: к основному интервалу относят все интервалы вида
разбивается на две части - основной интервал и дополнительный: к основному интервалу относят все интервалы вида 
 к дополнительному интервалу отнесем все остальные. Основные интервалы не пересекаются. Кроме того, для
к дополнительному интервалу отнесем все остальные. Основные интервалы не пересекаются. Кроме того, для 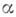 из основного интервала, сумма
из основного интервала, сумма  "близка" к рациональной сумме
"близка" к рациональной сумме  . Но при "малых"
. Но при "малых"  , известен закон распределения п. ч. в прогрессиях с разностью
, известен закон распределения п. ч. в прогрессиях с разностью  (напр., теорема Зигеля), т. е. известна асимптотика сумм
(напр., теорема Зигеля), т. е. известна асимптотика сумм  Так выделяется главный член проблемы, и в этом состоит идея кругового метода. Если теперь нетривиально оценить
Так выделяется главный член проблемы, и в этом состоит идея кругового метода. Если теперь нетривиально оценить  на дополнительных интервалах (см. Виноградова метод), то получится асимптотич. формула в проблеме Гольдбаха - Эйлера. См. также Круговой метод.
на дополнительных интервалах (см. Виноградова метод), то получится асимптотич. формула в проблеме Гольдбаха - Эйлера. См. также Круговой метод.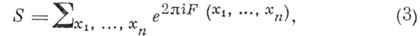
 - действительная функция, а
- действительная функция, а 
 пробегают множество целых чисел в количестве Р. Таким образом, центр тяжести многих проблем переносится на задачу изучения таких сумм, в частности на задачу получения возможно более точной оценки модуля таких сумм. Тривиальной оценкой суммы (3) будет Р. Ставится задача получить оценку типа
пробегают множество целых чисел в количестве Р. Таким образом, центр тяжести многих проблем переносится на задачу изучения таких сумм, в частности на задачу получения возможно более точной оценки модуля таких сумм. Тривиальной оценкой суммы (3) будет Р. Ставится задача получить оценку типа 
 наз. понижающим множителем. Первые нетривиальные оценки тригонометрич. сумм, когда
наз. понижающим множителем. Первые нетривиальные оценки тригонометрич. сумм, когда 
 - многочлен, а
- многочлен, а  получил Г. Вейль (1919), к-рый одновременно доказал критерий равнораспределенности дробных долей функции в терминах тригонометрич. сумм. Создателем метода тригонометрич. сумм является И. М. Виноградов, к-рый, используя глубокие арифметич. свойства рассматриваемых сумм, получил исключительно сильные оценки модуля широкого класса таких сумм. Это позволило ему получить фундаментальные близкие к предельно возможным результаты в целом ряде вопросов теории чисел (проблема Варинга, Гильберта- Камке проблема, Вейля суммы). Другим следствием метода Виноградова (1937) было решение ряда аддитивных проблем с п. ч. и, в частности, решение проблемы Гольдбаха - Эйлера. Основной идеей метода Виноградова является идея "сглаживания" (возведение в степень тригонометрич. суммы и сведение оценки к теореме о среднем при оценках сумм Вейля; введение двойных тригонометрич. сумм при оценках сумм с п. ч.). См. также Тригонометрических сумм метод.
получил Г. Вейль (1919), к-рый одновременно доказал критерий равнораспределенности дробных долей функции в терминах тригонометрич. сумм. Создателем метода тригонометрич. сумм является И. М. Виноградов, к-рый, используя глубокие арифметич. свойства рассматриваемых сумм, получил исключительно сильные оценки модуля широкого класса таких сумм. Это позволило ему получить фундаментальные близкие к предельно возможным результаты в целом ряде вопросов теории чисел (проблема Варинга, Гильберта- Камке проблема, Вейля суммы). Другим следствием метода Виноградова (1937) было решение ряда аддитивных проблем с п. ч. и, в частности, решение проблемы Гольдбаха - Эйлера. Основной идеей метода Виноградова является идея "сглаживания" (возведение в степень тригонометрич. суммы и сведение оценки к теореме о среднем при оценках сумм Вейля; введение двойных тригонометрич. сумм при оценках сумм с п. ч.). См. также Тригонометрических сумм метод.
 и
и  - тоже многочлены. Допуская, что
- тоже многочлены. Допуская, что  "хорошо" приближаются дробями
"хорошо" приближаются дробями  и
и  с достаточно большим
с достаточно большим  и
и 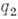 , полагая
, полагая 
 и доказывая, что
и доказывая, что  при
при 
 не обращается в нуль, получают противоречие. При доказательстве трансцендентности чисел А. О. Гельфонд строит функцию
не обращается в нуль, получают противоречие. При доказательстве трансцендентности чисел А. О. Гельфонд строит функцию 
 - алгебраич. число, при помощи принципа ящиков Дирихле целые не равные нулю числа
- алгебраич. число, при помощи принципа ящиков Дирихле целые не равные нулю числа  выбираются так, что
выбираются так, что  и "много" ее производных имеют "много" нулей. "Большое" количество нулей позволяет получить "хорошие" оценки сверху для "большого" числа производных и точек, а отсюда, при помощи оценок снизу, получаемых из теоремы Лиувилля, следует, что
и "много" ее производных имеют "много" нулей. "Большое" количество нулей позволяет получить "хорошие" оценки сверху для "большого" числа производных и точек, а отсюда, при помощи оценок снизу, получаемых из теоремы Лиувилля, следует, что 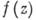 и "много" ее производных имеют больше нулей, чем вначале. Повторение этого процесса приводит к тому, что либо
и "много" ее производных имеют больше нулей, чем вначале. Повторение этого процесса приводит к тому, что либо  - рациональное число, либо
- рациональное число, либо  равны нулю, что противоречит их выбору. См. также Алгебраическое число, Трансцендентное число. Лит.:[1] Виноградов И. М., Избр. тр., М., 1952; [2]его же, Основы теории чисел, 7 изд., М., 1965; [3] его же, Метод тригонометрических сумм в теории чисел, М., 1971; [4] Гельфонд А. О., Трансцендентные и алгебраические числа, М., 1952; [5] Делове Б. Н., Петербургская школа теории чисел, М.-Л., 1947; [6] Карацуба А. А., Основы аналитической теории чисел, М., 1975; [7] Линвик Ю. В., Дисперсионный метод в бинарных аддитивных задачах, Л., 1961; [8] Чудаков Н. Г., Введение в теорию L-функций Дирихле, М.-Л., 1947; [9] Прахар К., Распределение простых чисел, пер. с нем., М., 1967; [10] Дэвенпорт Г., Мультипликативная теория чисел, пер. с англ., М., 1971; [11] Титчмарш Е., Теория дзета-функции Римана, пер. с англ., М., 1953; [12] Xуа Ло-ген, Метод тригонометрических сумм и его применения в теории чисел, пер. с нем., М., 1964; [13] Ваkеr A., "Mathematika", 1967, v. 14, №1(27), p. 102-07; [14] Виноградов А. И., "Изв. АН СССР. Серия матем.", 1965, т. 29, в. 4, с. 903-34; [15] Воmbiеri E., "Mathematiba", 1965, v. 12, №24, p. 201-25. А. А. Карацуба.
равны нулю, что противоречит их выбору. См. также Алгебраическое число, Трансцендентное число. Лит.:[1] Виноградов И. М., Избр. тр., М., 1952; [2]его же, Основы теории чисел, 7 изд., М., 1965; [3] его же, Метод тригонометрических сумм в теории чисел, М., 1971; [4] Гельфонд А. О., Трансцендентные и алгебраические числа, М., 1952; [5] Делове Б. Н., Петербургская школа теории чисел, М.-Л., 1947; [6] Карацуба А. А., Основы аналитической теории чисел, М., 1975; [7] Линвик Ю. В., Дисперсионный метод в бинарных аддитивных задачах, Л., 1961; [8] Чудаков Н. Г., Введение в теорию L-функций Дирихле, М.-Л., 1947; [9] Прахар К., Распределение простых чисел, пер. с нем., М., 1967; [10] Дэвенпорт Г., Мультипликативная теория чисел, пер. с англ., М., 1971; [11] Титчмарш Е., Теория дзета-функции Римана, пер. с англ., М., 1953; [12] Xуа Ло-ген, Метод тригонометрических сумм и его применения в теории чисел, пер. с нем., М., 1964; [13] Ваkеr A., "Mathematika", 1967, v. 14, №1(27), p. 102-07; [14] Виноградов А. И., "Изв. АН СССР. Серия матем.", 1965, т. 29, в. 4, с. 903-34; [15] Воmbiеri E., "Mathematiba", 1965, v. 12, №24, p. 201-25. А. А. Карацуба.