|
"
0
C
F
G
H
K
L
N
P
S
T
W
Z
А
Б
В
Г
Д
Е
Ж
З
И
Й
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Ш
Э
Ю
Я
ИНТЕГРАЛЗначение ИНТЕГРАЛ в математической энциклопедии: - одно из центральных понятий математич. анализа и всей математики, возникновение к-рого связано с двумя задачами: о восстановлении функции по ее производной (напр., с задачей об отыскании закона движения материальной точки вдоль прямой по известной скорости этой точки); о вычислении площади, заключенной между графиком функции f(x)на отрезке Указанные две задачи приводят к двум видам И.: неопределенному и определенному. Изучение свойств и вычисление этих связанных между собой видов И. составляет задачу интегрального исчисления. В ходе развития математики и под влиянием потребностей естествознания и техники понятия неопределенного и определенного И. подвергались ряду обобщений и изменений. Неопределенный интеграл. Первообразной функции f (х)одного переменного хна интервале а<х<b наз. любая функция F(x), производная к-рой для любого хиз этого интервала равна f(x). Очевидно, что если F(x)является первообразной функции f(x)нa интервале а<x<b, то и функция F1 (х)= F(x)+C, где С- любая постоянная, также является первообразной f(x)на этом интервале. Верно и обратное: любые две первообразные одной и той же функции f(x)на интервале a<x<b могут отличаться лишь на постоянную. Следовательно, если F(x)- одна из первообразных f(x)на интервале a<x<b, то любая первообразная f(x)на этом интервале имеет вид F(x)+C, где С- постоянная. Совокупность всех первообразных функции f (х)на интервале a<x<b наз. неопределенным интегралом функции f(x)(на этом интервале) и обозначается символом
Согласно основной теореме интегрального исчисления, для каждой непрерывной на интервале a<x<b функции f(х)существует на этом интервале первообразная и, следовательно, неопределенный И. Определенный интеграл. Понятие определенного И. вводится либо как предел интегральных сумм (см. Ноши интеграл, Римана интеграл, Лебега интеграл, Колмогорова интеграл, Стилтьеса интеграл), либо в случае, когда заданная функция f(x)определена на нек-ром отрезке [ а, b]и имеет на нем первообразную F, как разность ее значений на концах рассматриваемого отрезка F(b) - F(a). Определенный И. от функции f(x)на отрезке [ а, b] обозначают Между определенным И. от непрерывной на отрезке [а, b]функции f(x)и неопределенным И. (или первообразной) этой функции существует следующая связь: 1) если F(x)- любая первообразная функции f(x), то справедлива формула Ньютона - Лейбница
2) для любого хиз отрезка [ а, b] неопределенный И. непрерывной функции f(х)записывается в виде
где С- произвольная постоянная. В частности, определенный И. с переменным верхним пределом
представляет собой первообразную функцию f(х). Для введения определенного И. от функции f(x)по отрезку [ а, b]в смысле Лебега разбивают множество значений уна частичные отрезки точками ...<y_2<у -1<y0<у1<у2<... и обозначают через М i множество всех значений хиз отрезка [ а, b], для к-рых yi-1
где hi - любое число из отрезка Функцию f(x)наз. интегрируемой в смысле Лебега на отрезке [а, b], если существует предел ее интегральных сумм (2) при стремлении к нулю максимальной из разностей у i-yi-1, т. е. если существует такое число I, что для любого e>0 найдется d>0 такое, что при единственном условии Вместо отрезка [ а, b]можно рассматривать произвольное множество, измеримое относительно некоторой неотрицательной полной счетно аддитивной меры. Возможно и другое введение интеграла Лебега, когда этот И. первоначально определяют на множестве так наз. простых функций (т. е. измеримых функций, принимающих не более счетного множества значений), а затем с помощью операции предельного перехода вводят для произвольной функции, представляющей собой предел равномерно сходящейся последовательности простых функций (см. Лебега интеграл). Каждая интегрируемая в смысле Римана функция является интегрируемой и в смысле Лебега. Обратное неверно, ибо существуют разрывные на множестве положительной меры и вместе с тем интегрируемые в смысле Лебега функции (напр., функция Дирихле). Для интегрируемости по Лебегу ограниченной функции необходимо и достаточно, чтобы эта функция принадлежала классу измеримых функций. Функции, встречающиеся в математич. анализе, как правило, измеримы. Это означает, что интеграл Лебега обладает общностью, исчерпывающей потребности анализа. Интеграл Лебега охватывает и все случаи абсолютно сходящихся несобственных интегралов. Общность, достигнутая определением И. в смысле Лебега, весьма существенна во многих вопросах современного математич. анализа (теория обобщенных функций, определение обобщенных решений дифференциальных уравнений, изоморфизм гильбертовых пространств L2 и l2, эквивалентный так наз. теореме Рисса - Фишера в теории тригонометрических или произвольных ортогональных рядов,- все эти теории оказались возможными только при понимании И. в смысле Лебега). Первообразную в смысле Лебега естественно определить с помощью равенства (1), в к-ром И. понимается в смысле Лебега. При таком понимании соотношение F'(x)=f(x)будет справедливо всюду, кроме, может быть, множества, имеющего меру, равную нулю. Другие обобщения понятия интеграла. В 1894 Т. Стилтьесом (Т. Stieltjes) было дано другое важное для приложений обобщение интеграла Римана (получившее название интеграла Стилтьеса), в к-ром рассматривается интегрируемость одной функции f(x), определенной на некотором отрезке [a, b], относительно другой функции, определенной на том же отрезке. Интеграл Стилтьеса функции f(х)относительно функции U(х)обозначают символом
Если U(х)имеет ограниченную и интегрируемую в смысле Римана производную U'(х), то интеграл Стилтьеса сводится к интегралу Римана по формуле
в частности при и(х)=х+С интеграл Стилтьеса (3) является интегралом Римана Однако для приложений интересен случай, когда интегрирующая функция U(x)не имеет производной. Примером может служить рассмотрение в качестве U(x)спектральной меры при изучении спектральных разложений. Криволинейный интеграл
вдоль кривой Г, определяемой уравнениями x=j(t), y=y(t),
Дальнейшим обобщением понятия И. послужило интегрирование по произвольному множеству в пространстве любого числа измерений. В самом общем случае удобно рассматривать И. как функцию от того множества М, по к-рому производится интегрирование (см. Функции множеств )вида
где U- также некоторая функция множества М(в частном случае его мера), а точка принадлежит множеству М, по к-рому идет интегрирование. Частными случаями такого рассмотрения являются кратные интегралы и поверхностные интегралы. Другим обобщением понятия И. является понятие несобственного интеграла. В 1912 А. Данжуа (A. Denjoy) ввел понятие И. (см. Данжуа интеграл), применимое ко всякой функции f(x), являющейся производной нек-рой функции F(x). Это позволило привести конструктивное определение И. к такой степени общности, при к-рой оно целиком отвечает задаче разыскания неопределенного И., понимаемого в смысле первообразной. Лит.:[1] Ильин В. А., Позняк Э. Г., Основы математического анализа, ч. 1-2, М., 1971-73; [2] Колмогоров А. Н., Фомин СВ., Элементы теории функций и функционального анализа, 4 изд., М., 1976; [3] Кудрявцев Л. Д., Математический анализ, т. 1-2, 2 изд., М., 1973; [4] Никольский С. М., Курс математического анализа, т. 1-2, 2 изд., 1975; [5] Смирнов В. И., Курс высшей математики, т. 5, М., 1959; [6] Лебег А., Интегрирование и отыскание примитивных функций, пер. с франц., М.-Л., 1934. В. А. Илъин. А-ИНТЕГРАЛ - одно из обобщений интеграла Лебега, данное Е. Титчмаршем [1] для интегрирования функций, сопряженных к суммируемым. Измеримую функцию f(x)наз. А - интегрируемой на [ а, b], если
и существует предел
где
Число I наз. A-интегралом и обозначают
Лит.:[1]Titсhmаrsh E. G., "Proa London Math. Soc", 1929, № 29, с 49-80; [2] Виноградова И. А., Скворцов В. А., в кн.: Итоги науки. Математический анализ. 1970, М., 1971 , с. 65 - 107. И. А. Виноградова. |
|
|
|

 и осью абсцисс (к этой же задаче приводит вычисление работы, произведенной силой за промежуток времени
и осью абсцисс (к этой же задаче приводит вычисление работы, произведенной силой за промежуток времени  и другие вопросы).
и другие вопросы).
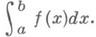 Определение И. как предела интегральных сумм в случае непрерывных функций было сформулировано О. Коши (А. Саuchy) в 1823. Случай произвольных функций был изучен Б. Риманом (В. Riemann, 1853). Существенное продвижение в теории определенного И. принадлежит Г. Дарбу (G. Darboux, 1879), к-рый ввел в рассмотрение наряду с интегральной суммой Римана верхнюю и нижнюю суммы (см. Дарбу сумма). Необходимое и достаточное условие интегрируемости по Риману разрывных функций в законченной форме установил (1902) А. Лебег (Н. Lebesgue).
Определение И. как предела интегральных сумм в случае непрерывных функций было сформулировано О. Коши (А. Саuchy) в 1823. Случай произвольных функций был изучен Б. Риманом (В. Riemann, 1853). Существенное продвижение в теории определенного И. принадлежит Г. Дарбу (G. Darboux, 1879), к-рый ввел в рассмотрение наряду с интегральной суммой Римана верхнюю и нижнюю суммы (см. Дарбу сумма). Необходимое и достаточное условие интегрируемости по Риману разрывных функций в законченной форме установил (1902) А. Лебег (Н. Lebesgue).

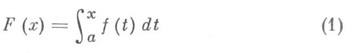
 f(x)<yi, а через m( М i) - меру множества М i в смысле Лебега. Интегральную сумму Лебега функции f(x)на отрезке [ а, b] определяют равенством
f(x)<yi, а через m( М i) - меру множества М i в смысле Лебега. Интегральную сумму Лебега функции f(x)на отрезке [ а, b] определяют равенством

 ( у i -у i-1)<d справедливо неравенство |s-I| <e. При этом указанный предел I наз. определенным интегралом Лебега от функции f(x)по отре. <зку [ а, b].
( у i -у i-1)<d справедливо неравенство |s-I| <e. При этом указанный предел I наз. определенным интегралом Лебега от функции f(x)по отре. <зку [ а, b].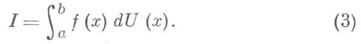



 представляет собой частный случай интегралa Стилтьеса, так как может быть записан в виде
представляет собой частный случай интегралa Стилтьеса, так как может быть записан в виде
 ,
,