|
"
0
C
F
G
H
K
L
N
P
S
T
W
Z
А
Б
В
Г
Д
Е
Ж
З
И
Й
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Ш
Э
Ю
Я
ИНДУЦИРОВАННОЕ РАССЛОЕНИЕЗначение ИНДУЦИРОВАННОЕ РАССЛОЕНИЕ в математической энциклопедии: - расслоение f* (p) : X' ->В', индуцированное отображением f : В'->В и расслоением p :
являются гомеоморфизмами. Кроме того, для любого расслоения h : Расслоения, индуцированные изоморфными расслоениями, изоморфны, расслоение, индуцированное постоянным отображением, изоморфно тривиальному. Для любого сечения sрасслоения p отображение s:
Лит.:[1] Годбийон К., Дифференциальная геометрия и аналитическая механика, пер. с франц., М., 1973; [2] Стинрод Н., Топология косых произведений, пер. с англ., М., 1953; [3] Xьюзмоллер Д., Расслоенные пространства, пер. с англ., М., 1970. М. И. Войцеховский. |
|
|
|
где X'- подпространство прямого произведения 
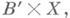состоящее из пар (b', х), для которых f(b')=p(х), а f* (p) - отображение, определяемое соответствием 
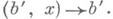Отображение F:
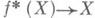И. р. в исходное расслоение, определенное формулой F(b', х) = х, является морфизмом расслоений, накрывающим f. Для каждой точки 
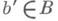ограничения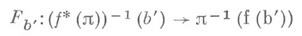
и морфизма Н:
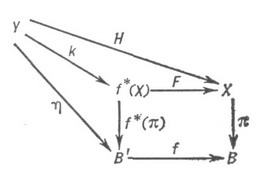
накрывающего f, существует один и только один В'-морфизм К: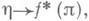
удовлетворяющий соотношениям FK=H,f*(p)K=h, так что имеет место коммутативная диаграмма:
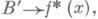определенное формулой s(b')= (b',sf(b')), является сечением И. р. f* (л) и удовлетворяет соотношению Fs=sf. Напр., отображение я :
индуцирует расслоение я 2 с пространством p*(х). и базой X- квадрат расслоения я, оно обладает единственным сечением s(x) = ( х, х).