|
"
0
C
F
G
H
K
L
N
P
S
T
W
Z
А
Б
В
Г
Д
Е
Ж
З
И
Й
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Ш
Э
Ю
Я
АНАЛИТИЧЕСКАЯ ПОВЕРХНОСТЬЗначение АНАЛИТИЧЕСКАЯ ПОВЕРХНОСТЬ в математической энциклопедии: абстрактная - двумерное комплексное аналитическое многообразие, т. е. четырехмерное гладкое многообразие, снабженное комплексной структурой. Хотя теория А. п. и является частью общей теории комплексных многообразий, двумерный случай выделяется особо, т. к. об А. п. известно гораздо больше, чем о я-мерных многообразиях при Все рассматриваемые в дальнейшем А. п. предполагаются компактными и связными. Примеры. 1) Алгебраические поверхности. Пусть набор однородных многочленов с комплексными коэффициентами. Замкнутое подмножество комплексного проективного пространства 2) Комплексные торы. Пусть 3) Поверхности Хопфа. Пусть Группа Zдействует дискретно и без неподвижных точек на Y, а факторпространство Классификация аналитических поверхностей. Основным инвариантом при классификации А. п. является степень трансцендентности поля мероморфных функций Для того чтобы А. п. Xбыла алгебраич. поверхностью, необходимо и достаточно, чтобы на Xсуществовали две алгебраически независимые мероморфные функции. Если А. п. Xобладает полем мероморфных функций степени трансцендентности 1, то Xявляется эллиптич. поверхностью, т. е. обладает голоморфным отображением на алгебраич. кривую и все слои отображения Р, кроме конечного числа, являются эллиптич. кривыми (особые слои могут иметь только очень специальный вид, к-рый хорошо изучен). Если на А. п. Xне существует мероморфных функций, кроме констант, и на Xнет исключительных кривых (см. Исключительное подмногообразие), то первое число Бетти b1 для Xможет принимать только три значения: 4, 1 и 0. При этом, если Кэлерова А. п. не всегда будет алгебраич. поверхностью. Однако это так, если квадрат ее первого Чжэня класса положителен. Каждая кэлерова А. п. с b1>0 является деформацией алгебраич. поверхности. Лит,.:[1] Кодаира К., "Математика", сб. переводов, 1962, т. 6, № 6, с. 3-17; [2] Коdairа К., "Ann. Math.", 1960, v. 71, p. 111 - 52; 1963, v. 77, p. 563-626; 1963, v. 78, p. 1-40; [3] его же, "Amer. J. Math.", 1964, v. 86, p. 751-98; 1966, v. 88, p. 682-721; 1968, v. 90, p. 55-83; 1048-66; [4] Алгебраические поверхности, М., 1965 ("Труды Матем. ин-та АН СССР", 1965, т. 75); [5] Шафаревич И. Р., Основы алгебраической геометрии, М., 1972. Б. Б. Венков. |
|
|
|

 Кроме того, нек-рые факты специфичны только для размерности 2. Эти специфич. результаты об А. п. касаются классификации А. п., аналогичной классификации алгебраических поверхностей, что в значительной степени сводит теорию А. п. к теории алгебраич. поверхностей. Основные результаты по классификации А. п. получены К. Кодаирой [1], [2], [3], к-рый, однако, опирался на работы классиков итальянской школы алгебраич. геометрии по классификации алгебраич. поверхностей.
Кроме того, нек-рые факты специфичны только для размерности 2. Эти специфич. результаты об А. п. касаются классификации А. п., аналогичной классификации алгебраических поверхностей, что в значительной степени сводит теорию А. п. к теории алгебраич. поверхностей. Основные результаты по классификации А. п. получены К. Кодаирой [1], [2], [3], к-рый, однако, опирался на работы классиков итальянской школы алгебраич. геометрии по классификации алгебраич. поверхностей.
 выделяемое уравнениями
выделяемое уравнениями  будет А. п., если оно неособо, связно и имеет комплексную размерность 2. Это - основной пример А. п.
будет А. п., если оно неособо, связно и имеет комплексную размерность 2. Это - основной пример А. п. - двумерное векторное пространство над полем комплексных чисел (как векторное пространство над полем действительных чисел оно изоморфно
- двумерное векторное пространство над полем комплексных чисел (как векторное пространство над полем действительных чисел оно изоморфно  ) и пусть
) и пусть  - решетка в
- решетка в  . Факторпространство
. Факторпространство  будет А. п. Как гладкое многообразие Xдиффеоморфно 4-мерному тору, однако комплексная структура на Xзависит от решетки Г. Комплексные торы
будет А. п. Как гладкое многообразие Xдиффеоморфно 4-мерному тору, однако комплексная структура на Xзависит от решетки Г. Комплексные торы  играют важную роль в анализе, так как мероморфные функции на них это мероморфиые функции на
играют важную роль в анализе, так как мероморфные функции на них это мероморфиые функции на  , к-рые периодичны с решеткой периодов Г. А. п. вида
, к-рые периодичны с решеткой периодов Г. А. п. вида  не всегда алгебра-ичпы. Существуют даже такие решетки Г, что на соответствующем торе
не всегда алгебра-ичпы. Существуют даже такие решетки Г, что на соответствующем торе 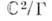 вообще нет мероморфных функций (кроме констант). Конкретные примеры таких торов можно найти в [5].
вообще нет мероморфных функций (кроме констант). Конкретные примеры таких торов можно найти в [5]. с - положительное число, п рассматривается действие группы Zна Y
с - положительное число, п рассматривается действие группы Zна Y 
 диффеоморфно
диффеоморфно  Факторпространство Xестественным образом является А. п., наз. поверхностью Хопфа.
Факторпространство Xестественным образом является А. п., наз. поверхностью Хопфа. на А. п. X. Согласно теореме Зигеля, для любого компактного связного комплексного многообразия Xполе
на А. п. X. Согласно теореме Зигеля, для любого компактного связного комплексного многообразия Xполе  конечно порождено и его степень трансцендентности не превышает комплексной размерности для X. Таким образом, для А. п. Xполе
конечно порождено и его степень трансцендентности не превышает комплексной размерности для X. Таким образом, для А. п. Xполе  может содержать две алгебраические независимые мероморфные функции, одну такую функцию или, вообще, состоять только из констант. В соответствии с этими возможностями имеют место следующие теоремы.
может содержать две алгебраические независимые мероморфные функции, одну такую функцию или, вообще, состоять только из констант. В соответствии с этими возможностями имеют место следующие теоремы. таким, что
таким, что 
 то Xявляется комплексным тором, а если
то Xявляется комплексным тором, а если  , то Xобладает тривиальным ка-нонич. расслоением. Последние А. п. наз. КЗ-поверхностями. Все они гомеоморфны между собой. Случай
, то Xобладает тривиальным ка-нонич. расслоением. Последние А. п. наз. КЗ-поверхностями. Все они гомеоморфны между собой. Случай  подробно не изучен, но известные примеры А. п. с
подробно не изучен, но известные примеры А. п. с  получаются обобщением конструкции поверхностей Хопфа.
получаются обобщением конструкции поверхностей Хопфа.