|
"
0
C
F
G
H
K
L
N
P
S
T
W
Z
А
Б
В
Г
Д
Е
Ж
З
И
Й
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Ш
Э
Ю
Я
ИНДЕКСА ФОРМУЛЫЗначение ИНДЕКСА ФОРМУЛЫ в математической энциклопедии: - соотношения между аналитич. и топологич. инвариантами операторов нек-рого класса. Именно, И. ф. устанавливают связь между аналитич. индексом линейного оператора
и измеряющим таким образом "разность" между дефектными подпространствами D:его ядром Кеr D=D-1(0) и его коядром Coker D = L1/D(L0), и топологич. индексом - нек-рой топологич. характеристикой оператора Dи пространств L0, L1. Для общего эллиптического дифференциального оператора на замкнутом многообразии задача нахождения И. ф. поставлена в конце 50-х гг. 20 в. [1] и решена в 1963 (см. [2]), хотя частные виды И. ф. были известны и ранее: такова, напр., Гаусса- Бонне теорема и ее многомерные варианты. В дальнейшем был получен ряд обобщений И. ф. на объекты более сложной природы; в этих случаях вместо индекса - целого числа - могут фигурировать произвольные комплексные числа и даже функции. Элементарные формулы индекса. 1) Пусть М- дифференцируемая граница ограниченной области
где х 1, . .., х п- локальные координаты . на М,x1, ..., xn - соответствующие координаты в касательном пространстве, S(M)- ориентированная граница В(М), образованная единичными касательными векторами. В силу эллиптичности Аего символ аявляется невырожденной (р
где 2) Пусть А- эллиптический дифференциальный оператор вида (здесь a- мультииндекс)
в пространстве
Набор операторов { А, В 1, . . ., B т/2}задает эллиптическую краевую задачу, если не вырождается на S(M)функция
а а + определяется из разложения а=а + а -, где
Формулы Атьи - Зингера. Пусть
где p :
где где ch V(s)- когомологический Чжэня характер расслоения V(s).
Теорема об индексе Атьи - Зингера:
Формула (2) допускает ряд модификаций. Вводится следующим образом зависящий от символа a(D)рациональный класс когомологий ch [s(D)]:тройке {p*(x), p* (h), s(D)}сопоставляется различающий элемент, к-рый можно рассматривать как первое препятствие к распространению изоморфизма а на все В(М),
где ТМ- касательное расслоение, к-рое (с помощью римановой метрики на М)можно отождествить с Т*М, K{B/S)- относительная группа Гротендика векторных расслоений над B/S, и следовательно - характер Чжэня
где л : Тома изоморфизм
позволяет записать (4) в виде
(в (4) и (5) справа по-прежнему, как и в (2), значения соответствующих элементов на фундаментальных циклах.) В терминах K-теории топологич. индекс выражается следующим образом. Пусть i:
Примеры. 3) Пусть М- замкнутое ориентированное риманово многообразие,
- оператор внешнего дифференцирования и его сопряженный, соответственно. 4) Пусть 5) Пусть h - голоморфное векторное расслоение над компактным комплексным многообразием М, x0,q - расслоение дифференциальных форм типа (0, q), Эллиптические комплексы. В более общей ситуации, естественно возникающей, напр., в дифференциальной геометрии, вместо одного оператора Dрассматривается комплекс (псевдодифференциальных) операторов
где xj - дифференцируемые векторные расслоения над замкнутым многообразием М, Dj+1Dj = 0. Символом комплекса Аназ. соответствующая последовательность главных символов
где p* (xj) - поднятие расслоений xj на S(M)с помощью проекции я :
где Hi (А)- группы когомологий комплекса А. Двумя важными примерами эллиптич. комплексов являются комплекс де Рама и его комплексный аналог - комплекс Дольбо. Проблема вычисления c(А)через класс комплекса s(А)в К( ТМ )может быть сведена к вычислению индекса для однако оператора [3]. Если компактная группа Gдействует на А(и коммутирует с действием Dj, т. е. Аесть G-комплекс), то Hj (А)будут G-модулями, и c(А). определяется как элемент кольца характеров группы G. Это - функция из Пусть G- топологическая циклическая группа, т. е. в Gсуществует элемент g, степени к-рого плотны в G, Ng- нормальное расслоение к Mg в М, и [s(A)]
где ind :
Без условия компактности G, но в предположении, что М g- нульмерное подмногообразие и действие Gявляется невырожденным (т. е. график gтрансверсален диагонали в М
Возможно, наконец, ослабление условия эллиптичности G-комплекса Арассмотрением так наз. трансверсально эллиптических комплексов; в этом случае индекс оказывается обобщенной функцией на группе G(cm. [8]). В частности, если G- конечна, то трансверсальная эллиптичность эквивалентна эллиптичности, так что применимы прежние формулы. Если M=G/H- однородное пространство, то все комплексы операторов трансверсально эллиптичны, и здесь И. ф. по существу совпадает с Фробениуса формулой взаимности для индуцированных представлений группы G., Нефредгольмовы операторы. В этом случае также иногда удается дать другое определение аналитич. индекса и получить соответствующие И. ф. Примеры: 6) Пусть D- равномерно эллиптич. оператор на Rn с почти периодич. коэффициентами. Аналитич. индекс ia(D)вводится с помощью относительной размерности в II-факторе (см. Неймана алгебра )и является действительным числом (см. [11]). Имеет место формула, аналогичная (1), но вместо интеграла по Rn в ней используется среднее значение почти периодич. функции. 7) Пусть на многообразии Мсвободно действует дискретная группа F' и факторпространство
где Р 1, Р 2- ортогональные проекторы на Ker Dи на Кеr D* в L2(M, dm),dm - любая Г-инвариантная гладкая плотность на М, а Тг Г Р для оператора Р, перестановочного с Г и имеющего гладкое ядро Р( х, у), определяется формулой
(здесь М 0- любая фундаментальная область группы Г на М,tr - след матрицы). Оказывается, что ia(D)) = 8) Если коэффициенты равномерно эллиптического оператора Dна Rn образуют однородное измеримое случайное поле, то можно ввести аналитич. индекс ia(D), являющийся случайной величиной (в эргодическом случае - действительным числом), определяемой по формуле (7) с заменой Тr Г Р на ТтР, где ТrР строится по ядру Р( х, у )оператора Рчерез среднее значение по х:Тг Р=М x{tr Р( х, х)}. Этот пример - обобщение (х6) и для него имеет место [14] аналогичная И. ф. Если дано семейство эллиптических операторов, параметризованное точками укомпактного пространства Y, то определен его аналитич. индекс Лит.:[1] Гельфанд И. М., "Успехи матем. наук", 1960, т. 15, в. 3, с. 121-32; [2] Атья М. Ф., 3ингер И. <М., "Математика", 1966, т. 10, № 3, с. 29-38; [3] их же, "Успехи матем. наук", 1968, т. 23, в. 5, с. 99-142; [4] Атья М. Ф., Сегал Г. Б., там же, в. 6, с. 135-49; [5] Атья М. Ф., Зингер И. М., там же, 1969, т. 24, в. 1, с. 127-82; [8] и х же, там же, 1972, т. 27, в. 4, с. 161-88; [7] Федосов Б. В., "Тр. Моск. матем. об-ва", 1974, т. 30, с. 159-241; [8] Atiуah M., Elliptic operators and compact groups, В.-Hdlb.- N.Y., 1974; [9] Пале Р., Семинар по теореме Атьи - Зингера об индексе, пер. с англ., М., 1970; [10] Атья М. Ф., Ботт Р., Патоди В. К., "Математика", 1973, т. 17, № 6, с. 3-48; [11] Coburn L., Moyer R., Singer I. M., "Acta Math.", 1973, v. 130, № 3-4, p. 279-307; [12] Atiyah M. P., "Asterisque", 1976, v. 32-33, p. 43 - 72; [13] Atiyah M. F., Schmid W., "Inventiones math.", 1977, v. 42, p. 1-62; [14] Федосов Б. В., Шубин М. А., "Докл. АН СССР", 1977, т. 236, № 4, с. 812 -5; [15] АтьяМ. Ф., Лекции по К-теории, пер. с англ., М., 1967; [1б] Boutet de Monvel L., "Acta math.", 1971, v. 126, № 1-2, p. 11-51; [17] Федосов Б. В., "Матем. сб.", 1974, т. 93, №1, с. 62-89; т. 95, № 4, с. 525 - 50; 1976, т. 101, № 3, с. 380-401. М. И. Войцеховский, М. А. Шубин. |
|
|
|

 (L0, L1- топологич. векторные пространства), определяемым формулой
(L0, L1- топологич. векторные пространства), определяемым формулой
 А- эллиптический псевдодифференциальный оператор, отображающий пространство
А- эллиптический псевдодифференциальный оператор, отображающий пространство  дифференцируемых комшгекенозначных вектор-функций на Мсо значениями в С р в себя. Пусть В(М)- многообразие касательных векторов к Мдлины
дифференцируемых комшгекенозначных вектор-функций на Мсо значениями в С р в себя. Пусть В(М)- многообразие касательных векторов к Мдлины  ориентированное посредством 2n-формы
ориентированное посредством 2n-формы
 р)-матричной функцией на S(M). Оказывается, что для индекса оператора Аимеет место формула [7]:
р)-матричной функцией на S(M). Оказывается, что для индекса оператора Аимеет место формула [7]:
 - внешняя степень матричной дифференциальной формы a-1da, а через Тr обозначен след (р
- внешняя степень матричной дифференциальной формы a-1da, а через Тr обозначен след (р  р)-матричной формы. В частности, если р<n или если А- дифференциальный оператор на нечетномерном многообразии, то ind A = 0 (для псевдодифференциального оператора последнее, вообще говоря, неверно).
р)-матричной формы. В частности, если р<n или если А- дифференциальный оператор на нечетномерном многообразии, то ind A = 0 (для псевдодифференциального оператора последнее, вообще говоря, неверно).
 В 1, . . ., В т/2,- краевые дифференциальные операторы из
В 1, . . ., В т/2,- краевые дифференциальные операторы из  в
в 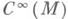 вида
вида
 Здесь rjk - коэффициенты полиномов
Здесь rjk - коэффициенты полиномов  являющихся остатками от деления l-полиномов bj(x, l) на l-полином а +(x, l), где
являющихся остатками от деления l-полиномов bj(x, l) на l-полином а +(x, l), где

 x, v - единичные касательный вектор и внутренняя нормаль к Мсоответственно; а + (соответственно а -)- l-полином, не имеющий нулей в верхней (соответственно, нижней) l-полуплоскости. Индексом описанной краевой задачи наз. индекс соответствующего ей линейного оператора
x, v - единичные касательный вектор и внутренняя нормаль к Мсоответственно; а + (соответственно а -)- l-полином, не имеющий нулей в верхней (соответственно, нижней) l-полуплоскости. Индексом описанной краевой задачи наз. индекс соответствующего ей линейного оператора  из
из  в
в  переводящего
переводящего  в набор {Аи, В1u|M, . . ., В т/2 и|M}. Оказывается, что индекс эллиптической краевой задачи совпадает с индексом эллиптического псевдодифференциального оператора на М, символом к-рого служит матрица r=(rjk). В частности, индекс задачи Дирихле
в набор {Аи, В1u|M, . . ., В т/2 и|M}. Оказывается, что индекс эллиптической краевой задачи совпадает с индексом эллиптического псевдодифференциального оператора на М, символом к-рого служит матрица r=(rjk). В частности, индекс задачи Дирихле  равен нулю. Имеются общие И. ф. для граничных задач [16], [17].
равен нулю. Имеются общие И. ф. для граничных задач [16], [17]. и С°° (h).- пространства бесконечно дифференцируемых сечений векторных расслоений x и h. над дифференцируемым замкнутым n-мерным многообразием М, D- (псевдодифференциальный) эллиптич. оператор, действующий из
и С°° (h).- пространства бесконечно дифференцируемых сечений векторных расслоений x и h. над дифференцируемым замкнутым n-мерным многообразием М, D- (псевдодифференциальный) эллиптич. оператор, действующий из  в
в  Топологич. индекс it(D)оператора Dопределяется следующим образом. Вследствие эллиптичности символ s(D). оператора Dопределяет изоморфизм поднятий векторных расслоений на S(M):
Топологич. индекс it(D)оператора Dопределяется следующим образом. Вследствие эллиптичности символ s(D). оператора Dопределяет изоморфизм поднятий векторных расслоений на S(M):
 - расслоение единичных сфер кокасательного расслоения Т*М многообразия М. Пусть В(М)- пространство расслоения единичных шаров в Т*М, это - 2n-мерное многообразие с краем S(M). Склейкой двух экземпляров В + (М)и В~ (М)многообразия В(М)по их общей границе получается замкнутое 2n-мерное многообразие е(М) = В +US(M)B- , над к-рым строится векторное расслоение
- расслоение единичных сфер кокасательного расслоения Т*М многообразия М. Пусть В(М)- пространство расслоения единичных шаров в Т*М, это - 2n-мерное многообразие с краем S(M). Склейкой двух экземпляров В + (М)и В~ (М)многообразия В(М)по их общей границе получается замкнутое 2n-мерное многообразие е(М) = В +US(M)B- , над к-рым строится векторное расслоение
 a s(D). использовано для отождествления x и h вдоль S(M). Это векторное расслоение V(s). несет всю топологич. информацию, нужную для определения топологич. индекса. Именно:
a s(D). использовано для отождествления x и h вдоль S(M). Это векторное расслоение V(s). несет всю топологич. информацию, нужную для определения топологич. индекса. Именно:
 когомологический Тодда класс комплексифицированного кокасательного расслоения
когомологический Тодда класс комплексифицированного кокасательного расслоения и справа стоит значение 2n-мерной компоненты элемента ch
и справа стоит значение 2n-мерной компоненты элемента ch на фундаментальном цикле многообразия [е(М)]. Таким образом, отображение V(s(D))->it(D). определяет гомоморфизм
на фундаментальном цикле многообразия [е(М)]. Таким образом, отображение V(s(D))->it(D). определяет гомоморфизм  тривиальный на образе К(М), здесь К(Х)- Гротендика группа, порожденная комплексными векторными расслоениями над X.
тривиальный на образе К(М), здесь К(Х)- Гротендика группа, порожденная комплексными векторными расслоениями над X.

 Теперь формула для топологич. индекса Dпринимает вид:
Теперь формула для топологич. индекса Dпринимает вид:



 - дифференцируемое вложение М в евклидово пространство, W- трубчатая окрестность Мв Е, к-рую можно рассматривать как действительное векторное расслоение над М, причем TW изоморфно (над R)
- дифференцируемое вложение М в евклидово пространство, W- трубчатая окрестность Мв Е, к-рую можно рассматривать как действительное векторное расслоение над М, причем TW изоморфно (над R)  - комплексификации расслоения W, поднятой на ТМ проекцией я :
- комплексификации расслоения W, поднятой на ТМ проекцией я : Композиция изоморфизма Тома
Композиция изоморфизма Тома  с естественным гомоморфизмом
с естественным гомоморфизмом  индуцированным вложением
индуцированным вложением  определяет гомоморфизм i! :
определяет гомоморфизм i! :  Пусть b:
Пусть b: -изоморфизм периодичности Ботта. Тогда гомоморфизм boi!, :
-изоморфизм периодичности Ботта. Тогда гомоморфизм boi!, : не зависит от вложения, и
не зависит от вложения, и
 - расслоение комплексных дифференциальных k-форм над М,
- расслоение комплексных дифференциальных k-форм над М,
 Оператор где
Оператор где 
 эллиптичен, для него справедлива И. ф. ('6), причем топологич. индекс равен эйлеровой характеристикеc(М). (Ходжа - де Рама теорема). При dim M=2 получается теорема Гаусса - Бонне.
эллиптичен, для него справедлива И. ф. ('6), причем топологич. индекс равен эйлеровой характеристикеc(М). (Ходжа - де Рама теорема). При dim M=2 получается теорема Гаусса - Бонне. - собственные
- собственные  -пространства инволюции I(a)=ip(p-1)+k*a,
-пространства инволюции I(a)=ip(p-1)+k*a, где * есть оператор двойственности, определяемой метрикой на М, dim M=2k. Сужение оператора d+d* до оператора из
где * есть оператор двойственности, определяемой метрикой на М, dim M=2k. Сужение оператора d+d* до оператора из  в
в  называемое сигнатурным оператором dM- эллиптический оператор, для него справедлива ,И. ф. (3), причем аналитич. индекс равен сигнатуре многообразия М, а топологич. индекс равен L-роду (теорема Хирцебруха).
называемое сигнатурным оператором dM- эллиптический оператор, для него справедлива ,И. ф. (3), причем аналитич. индекс равен сигнатуре многообразия М, а топологич. индекс равен L-роду (теорема Хирцебруха). - расслоение форм типа (0, q)с коэффициентами в h, z0,q - С-модуль гладких сечений этого расслоения. Пусть
- расслоение форм типа (0, q)с коэффициентами в h, z0,q - С-модуль гладких сечений этого расслоения. Пусть  - оператор Коши - Римана - Дольбо,
- оператор Коши - Римана - Дольбо,  - его сопряженный,
- его сопряженный,
 Тогда оператор
Тогда оператор  является эллиптическим, и для него справедливо (3), причем аналитич. индекс равен эйлеровой характеристике М с коэффициентами в пучке ростков голоморфных сечений расслоения h, а топологический индекс -
является эллиптическим, и для него справедливо (3), причем аналитич. индекс равен эйлеровой характеристике М с коэффициентами в пучке ростков голоморфных сечений расслоения h, а топологический индекс -  где ch h - характер Чжэня расслоения h,
где ch h - характер Чжэня расслоения h, - класс Тодда касательного расслоения к М(теорема Римана - Роха - Хирцебруха).
- класс Тодда касательного расслоения к М(теорема Римана - Роха - Хирцебруха).

 Комплекс Аназ. эллиптическим, если его символ является ациклическим комплексом, т. е. точен всюду вне нулевого сечения. Аналитическим индексом комплекса A наз. его эйлерова характеристика:
Комплекс Аназ. эллиптическим, если его символ является ациклическим комплексом, т. е. точен всюду вне нулевого сечения. Аналитическим индексом комплекса A наз. его эйлерова характеристика:
 Оказывается при этом, что теорема об индексе может рассматриваться как обобщение Лефшеца теоремы о неподвижных точках, поскольку топологич. индекс в точке
Оказывается при этом, что теорема об индексе может рассматриваться как обобщение Лефшеца теоремы о неподвижных точках, поскольку топологич. индекс в точке  может быть выражен через индекс сужения символа на подмножество
может быть выражен через индекс сужения символа на подмножество  неподвижных точек -отображения, задаваемого элементом g.
неподвижных точек -отображения, задаваемого элементом g. KG(TM)- класс символа А. Пусть i*[s(A)](g).
KG(TM)- класс символа А. Пусть i*[s(A)](g). К G(TMS). и
К G(TMS). и  - ограничение на Mg его и класса, порожденного стандартным комплексом внешних степеней расслоения
- ограничение на Mg его и класса, порожденного стандартным комплексом внешних степеней расслоения  соответственно (здесь i:
соответственно (здесь i: я : ТМ g->М g). Тогда число Лефшеца L(g, А), равное е(-1)j Tr(g|Hj(A)), задается формулой:
я : ТМ g->М g). Тогда число Лефшеца L(g, А), равное е(-1)j Tr(g|Hj(A)), задается формулой:
 _- естественное расширение топологич. индекса
_- естественное расширение топологич. индекса  Когомологический вариант этой формулы:
Когомологический вариант этой формулы:
 М), имеет место аналогичная формула. Она может быть выражена таким образом. Если
М), имеет место аналогичная формула. Она может быть выражена таким образом. Если  то dg(P)оставляет на место ТМ| Р,a gиндуцирует в слое xj|P линейное преобразование lj(g, P), и
то dg(P)оставляет на место ТМ| Р,a gиндуцирует в слое xj|P линейное преобразование lj(g, P), и
 компактно; пусть x, h - векторные расслоения над Ми Г действует на них согласованно с ее действием па М. Для эллиптич. оператора D:
компактно; пусть x, h - векторные расслоения над Ми Г действует на них согласованно с ее действием па М. Для эллиптич. оператора D: на М, перестановочного с действием Г, аналитич. индекс определяется формулой
на М, перестановочного с действием Г, аналитич. индекс определяется формулой

 где
где  - оператор на
- оператор на  символ к-рого s(D). индуцирует s(D). при поднятии на Мс помощью канонической проекции p :
символ к-рого s(D). индуцирует s(D). при поднятии на Мс помощью канонической проекции p :  [12]. Таким образом И. ф. для оператора Dможет быть получена из И. ф. для оператора Dна компактном многообразии М. Этот результат позволяет обнаруживать нетривиальность пространств, в к-рых реализуются представления дискретных серий [13].
[12]. Таким образом И. ф. для оператора Dможет быть получена из И. ф. для оператора Dна компактном многообразии М. Этот результат позволяет обнаруживать нетривиальность пространств, в к-рых реализуются представления дискретных серий [13]. (см. [15]). Топологич. индекс it(D)строится аналогично формуле (6) (все построения делаются "послойно" над Y). и имеет место теорема об индексе.
(см. [15]). Топологич. индекс it(D)строится аналогично формуле (6) (все построения делаются "послойно" над Y). и имеет место теорема об индексе.