" 0 C F G H K L N P S T W Z А Б В Г Д Е Ж З И Й К Л М Н О П Р С Т У Ф Х Ц Ч Ш Э Ю Я

ИНВАРИАНТНОЕ ПОДПРОСТРАНСТВО

Значение ИНВАРИАНТНОЕ ПОДПРОСТРАНСТВО в математической энциклопедии:

представления p группы (алгебры, кольца, полугруппы) Xв векторном пространстве (соответственно в топологич. векторном пространстве) Е- векторное (соответственно замкнутое векторное) подпространство такое, что для любого 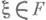и любоговыполняется соотношение: Если Р- проектор в Ена F, то Fтогда и только тогда является И. п. представления я, когда Рp(х) Р=p(х) Р для всех Подпространства {0} и Еявляются И. п. для любого представления в пространстве Е;. они наз. тривиальными И. п.; остальные И. п. (если они есть) наз. нетривиальными. См. также Сужение представления, Вполне приводимое множество, Неприводимое представление.

А. <И. <Штерн.