|
"
0
C
F
G
H
K
L
N
P
S
T
W
Z
А
Б
В
Г
Д
Е
Ж
З
И
Й
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Ш
Э
Ю
Я
ИНВАРИАНТЗначение ИНВАРИАНТ в математической энциклопедии: - отображение j рассматриваемой совокупности М математич. объектов, снабженной фиксированным отношением эквивалентности р, в другую совокупность Nматематич. объектов, постоянное на классах эквивалентности Мпо r(точнее: И. отношения эквивалентности р на М). Если X- объект из М, то весьма часто говорят, что j(М).- И. объекта X. Концепция И. является одной из важнейших в математике, поскольку изучение И. непосредственно связано с задачами классификации объектов того или иного типа. По существу, целью всякой математич. классификации является построение нек-рой полной системы И. (по' возможности, наиболее простой), то есть такой системы, к-рая разделяет любые два неэквивалентных объекта из рассматриваемой совокупности. Простейшим примером И. могут служить так наз. И. действительных плоских линий второго порядка. А именно, пусть М- множество всех таких линий, r - отношение эквивалентности на М, определенное правилом:
не зависят от выбора системы координат (хотя само уравнение линии Г - зависит). Если две линии Другой классич. пример - двойное отношение упорядоченного набора четырех точек, лежащих на одной прямой в действительном проективном пространстве. Двойное отношение не изменится, если подвергнуть эти точки проективному преобразованию всего пространства. В этом примере: М- это множество упорядоченных четверок точек проективного пространства, лежащих на одной прямой; отношение эквивалентности р на М - определяется по правилу: наборы Fи Сопоставление квадратичной форме от ппеременных ее ранга также доставляет пример И.: ранг не меняется при замене формы на эквивалентную (коротко: ранг есть И. квадратичной формы). Более того, если формы рассматриваются над полем комплексных чисел, то ранг составляет полную систему И. форм от ппеременных - две формы эквивалентны тогда и только тогда, когда их ранги равны. Если же рассматривать формы над полем действительных чисел, то появляется еще один И.- сигнатура формы; ранг и сигнатура соcтавляют полную систему И, В этих примерах М- множество квадратичных форм от ппеременных, r - отношение эквивалентности, определенное невырожденными линейными преобразованиями переменных, N- множество целых чисел. Общая черта, объединяющая эти (и многие другие) примеры, состоит в том, что отношение эквивалентности р определяется с помощью нек-рой группы Gпреобразований множества М(т. е. X и Однако общее понятие И. является более широким и не может быть ограничено рамками И. групп преобразований, поскольку не всегда отношение эквивалентности р на рассматриваемом множестве Мматематич. объектов определено действием группы. Примеры И. такого типа можно указать во многих областях математики. В алгебраич. и гомотопич. топологии каждому топологич. пространству сопоставляют его гомотопич. группы, а также группы сингулярных гомологии (с коэффициентами в нек-рой группе); эти группы являются И. относительно гомотопич. эквивалентности пространств. В алгебраич. геометрии рассматривается отношение бирациональной эквивалентности алгебраич. многообразий; размерность многообразия и, если ограничиться рассмотрением гладких полных многообразий, арифметич. род дают примеры И. этого отношения эквивалентности. В дифференциальной топологии многообразия рассматриваются с точностью до диффеоморфизма; классы Штифеля - Уитни многообразия являются И. относительно этого отношения эквивалентности. В классической дифференциальной геометрии рассматривается полная кривизна поверхности; она является И. изгибания. В теории абелевых групп рассматриваются так наз. И. конечно порожденных групп - ранг и порядки примерных компонент; они составляют полный набор И. для множества таких групп, рассматриваемых с точностью до изоморфизма. В. Л. Попов. Arf-ИНВАРИАНТ, инвариант Арфа,- инвариант квадратичной формы по модулю 2, заданной на целочисленной решетке, снабженной билинейной кососимметрич. формой. Пусть П - целочисленная решетка размерности k=2т и y( х, у)- форма, для к-рой y( х, y)=-y(y, х). Имеются базисы вида {е 1, f1, . . ., е т, fm}, наз. симплектическими, в к-рых матрица формы y(х, у)приводится к блочнодиагональному виду: по диагонали стоят блоки y(ei,fi)=-y(fi, ei)=1. а в других местах - нули. Пусть на П задано отображение
для к-рого y0( х, y)=y0(x)+y0(y)+y(x, у)mod 2 - "квадратичная форма по модулю 2". Выражение
и наз. инвариантом Арфа [1]. Если это выражение равно нулю, то существует симплектический базис, на всех элементах к-рого форма y0 равна нулю, если же это выражение равно единице, то существует симплектический базис, на всех элементах к-рого, кроме е 1 и f1, форма равна нулю, в то время как Лит.:[1] Arf С, "J. reine und angew. Math.", 1941, Bd 183, S. 148-67. А. В. Чернавский. |
|
|
|

 эквивалентна
эквивалентна  тогда и только тогда, когда Г' получается из Г движением (т. е. изометрией) плоскости. Если Ax2+2Bxy+Cy2+2Dx+2Ey+F=0- уравнение линии
тогда и только тогда, когда Г' получается из Г движением (т. е. изометрией) плоскости. Если Ax2+2Bxy+Cy2+2Dx+2Ey+F=0- уравнение линии  в какой-либо декартовой системе координат, то числа s(Г)=А+С,
в какой-либо декартовой системе координат, то числа s(Г)=А+С,  и
и 
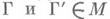 эквивалентны, то s(Г),=s(Г'), d(Г)=d(Г') и D(Г)=D(Г'). Иначе говоря, отображения s, d и D множества Мв множество Nвсех действительных чисел являются И. отношения эквивалентности r - эти отображения и называют И. действительных плоских линий второго порядка. Значения этих И. на конкретной линии позволяют определить тип этой линии (эллипс, гипербола, парабола, пара прямых, мнимая кривая).
эквивалентны, то s(Г),=s(Г'), d(Г)=d(Г') и D(Г)=D(Г'). Иначе говоря, отображения s, d и D множества Мв множество Nвсех действительных чисел являются И. отношения эквивалентности r - эти отображения и называют И. действительных плоских линий второго порядка. Значения этих И. на конкретной линии позволяют определить тип этой линии (эллипс, гипербола, парабола, пара прямых, мнимая кривая). эквивалентны тогда и только тогда, когда Fпереводится в F' проективным преобразованием пространства; N- множество действительных чисел. Взятие двойного отношения определяет отображение Мв N, являющееся И. отношения р; именно в этом смысле говорят, что двойное отношение - И. четырех точек (относительно проективной группы).
эквивалентны тогда и только тогда, когда Fпереводится в F' проективным преобразованием пространства; N- множество действительных чисел. Взятие двойного отношения определяет отображение Мв N, являющееся И. отношения р; именно в этом смысле говорят, что двойное отношение - И. четырех точек (относительно проективной группы). р-эквивалентны тогда и только тогда, когда Y-g(X)для нек-рого
р-эквивалентны тогда и только тогда, когда Y-g(X)для нек-рого  ); И., возникающие в таких случаях, наз. И. группы G. В первом примере - это преобразования М, индуцированные группой изометрий плоскости, во втором - проективной группой, в третьем - полной линейной группой невырожденных преобразований переменных. Эти примеры иллюстрируют общую концепцию, выдвинутую Ф. Клейном (F. Klein) (так наз. эрлангенская программа), согласно к-рой всякая группа преобразований может служить группой "преобразований систем координат" (автоморфизмов) в некоторой геометрии; величины, определяемые объектами этой геометрии и не меняющиеся при "смене координат" (инварианты), описывают внутренние свойства рассматриваемой геометрии и дают "структурную" классификацию ее теорем. Так, напр., задача проективной геометрии - нахождение И. (и соотношений между ними) для проективной группы, евклидовой геометрии - для группы движений (изометрий) евклидова пространства и т. д. На этом пути возникла классическая инвариантов теория, в к-рой рассматриваются лишь И. специального вида (полиномиальные или рациональные И. для групп линейных преобразований или, шире, числовые функции, постоянные на орбитах нек-рой группы).
); И., возникающие в таких случаях, наз. И. группы G. В первом примере - это преобразования М, индуцированные группой изометрий плоскости, во втором - проективной группой, в третьем - полной линейной группой невырожденных преобразований переменных. Эти примеры иллюстрируют общую концепцию, выдвинутую Ф. Клейном (F. Klein) (так наз. эрлангенская программа), согласно к-рой всякая группа преобразований может служить группой "преобразований систем координат" (автоморфизмов) в некоторой геометрии; величины, определяемые объектами этой геометрии и не меняющиеся при "смене координат" (инварианты), описывают внутренние свойства рассматриваемой геометрии и дают "структурную" классификацию ее теорем. Так, напр., задача проективной геометрии - нахождение И. (и соотношений между ними) для проективной группы, евклидовой геометрии - для группы движений (изометрий) евклидова пространства и т. д. На этом пути возникла классическая инвариантов теория, в к-рой рассматриваются лишь И. специального вида (полиномиальные или рациональные И. для групп линейных преобразований или, шире, числовые функции, постоянные на орбитах нек-рой группы). , т. е.
, т. е.

